巧用“肉夹馍”突破曲线运动

张通礼

一、巧用“肉夹馍”确定物体的曲线运动情况

曲线运动是变速运动，从运动学的角度可以确定物体加速度与速度、轨迹之间的关系，也可以从动力学的角度确定合外力F与速度、轨迹之间的关系。

所谓“肉夹馍”就是指加速度（或合外力）与速度这两个外面的“馍”把轨迹夹在中间，轨迹就是其中香喷喷的“肉馅物体的轨迹仅与物体的速度和加速度的大小、方向有关，由“馍”决定。物体做曲线运动的轨迹总夹在a与ν两方向的夹角中，且向加速度（或合外力）一侧弯曲。物体做曲线运动的轨迹有以下三种情况：物体的加速度a与速度ν之间的夹角为锐角、直角或钝角，物体分别做加速、匀速、减速曲线运动，如图1所示。

例1 一个物体沿y轴下落，下落到0点时突然受到沿x轴正方向、跟重力大小相等的恒定的水平风力作用，以下四幅图中最有可能正确反映物体的运动轨迹的是（ ）

解析 物体落到0点时，其速度方向（轨迹的切线方向）为竖直向下，而重力和风力的合力与x轴成45°角斜向下，所以物体做曲线运动且轨迹“肉馅”始终夹在合力与该时刻速度方向这两个“馍”之间，且向合力方向弯曲，而B选项中后半部分并没满足“肉夹馍”模型，所以只有C对。

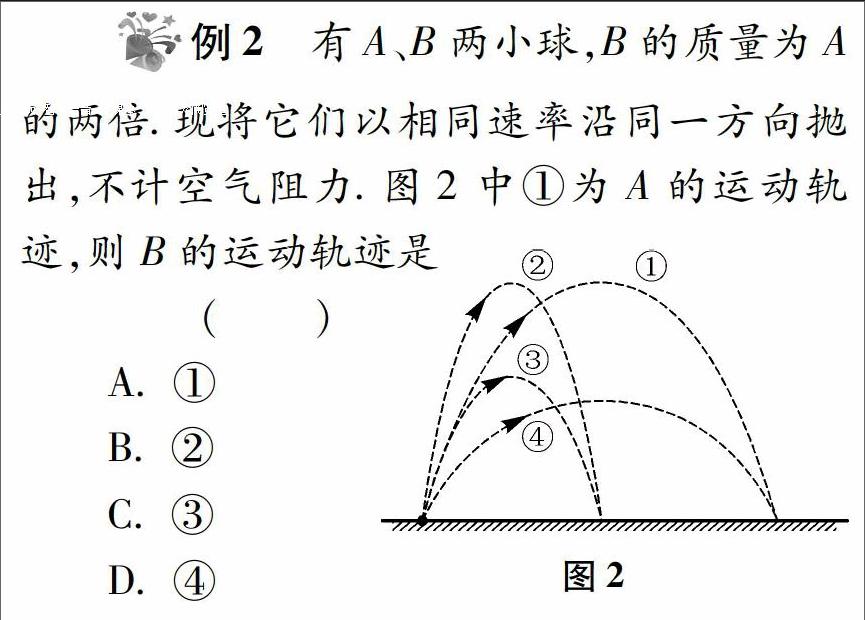
例2有A、B两小球，B的质量为A的两倍。现将它们以相同速率沿同一方向抛出，不计空气阻力。图2中①为A的运动轨迹，则B的运动轨迹是（ ）

A.①

B.②

C.③

D.④

解析

由题意知A、B两小球拋出的初速度相同，由牛顿第二定律知，两小球运动的加速度相同，小球的运动轨迹这个肉馅是由速度及加速度大小及方向的“馍”决定，所以运动的轨迹完全相同，故A正确。

二、巧用“肉夹馍”处理平抛运动、匀速圆周运动问题

平抛运动、勾速圆周运动是典型的曲线运动，拋物线及圆周的轨迹与速度、加速度的方向的关系均属于“肉夹馍”模型的实例。处理这两种运动的核心是加深对两边“馍”（速度与加速度或合力）的理解，即将速度这个“馍”沿合力方向和垂直合力方向两个方向分开。力是改变运动状态的原因，所以在垂直力方向上的分速度将保持不变。 引探导航。难点突破

1.平抛运动的处理

解决平拋问题，首先大致画出拋物线这个“馅”，其次画出合速度的方向（切线）、重力的方向这两个“馍”，最后分解掰开速度这个“馍许多学生没有养成画“馅”和“馍”的习惯，没有使抽象的问题具体形象化，导致不能深人理解平拋的规律。

例3如图4，圆弧形凹槽固定在水平地面上，其中ABC是位于竖直平面内以0为圆心的一段圆弧，0A与竖直方向的夹角为α。一小球以速度ν₀从桌面边缘P水平抛出，恰好从A点沿圆弧的切线方向进入凹槽。小球从P到A的运动时间为_______。

解析 据题意，小球从p点拋出后做平拋运动，小球运动到A点时画出两个“馍”，同时将速度这个“馍”分解，有

，则小球运动到A点的时间为

2.匀速圆周运动的处理

匀速圆周运动是变速曲线运动，必须先定圆心，画出向心加速度的方向即确定两“馍”的方向（两“馍”的方向彼此垂直）。然后受力分析，以两“馍”的方向建立坐标系进行正交分解，用牛顿第二定律列方程。

例4 如图5所示为赛车场的一个水平“梨形”赛道，两个弯道分别为半径R=90m的大圆弧和r=40m的小圆弧，直道与弯道相切。大、小圆弧圆心O、0距离L=100m。赛车沿弯道路线行驶时，路面对轮胎的最大径向静摩擦力是赛车重力的2.25倍。假设赛车在直道上做勾变速直线运动，在弯道上做勾速圆周运动。要使赛车不打滑，绕赛道一圈时间最短（发动机功率足够大，重力加速度g取10m/s²，π=3.14），则赛车（ ）

A.在绕过小圆弧弯道后加速

B.在大圆弧弯道上的速率为45m/s

C.在直道上的加速度大小为5.63m/s²

D.通过小圆弧弯道的时间为5.58s

解析 在弯道上做匀速圆周运动时，找出大、小弯道的圆心，画出两“馍”的方向，要使赛车绕赛道一圈时间最短，则通过弯道的速度都应最大。沿两“馍”的方向建立坐标系，根据牛顿定律

，通过小弯道的速度ν₁=30m/s，通过大弯道的速度ν₂=45m/s，故绕过小圆弧弯道后要加速，選项A、B正确；如图5，由几何关系可得endprint