基于核偏最小二乘的光伏发电出力预测

胡 益

(华东电力设计院有限公司，上海 200237)

1 概述

随着新能源的不断开发和利用，光伏发电工程呈现出快速增长的趋势，目前已有多个大型光伏电站建成并投入运行。由于并网光伏发电系统的出力具有间歇性和不可控性等缺点，其对电力系统的安全稳定运行会造成冲击，因此有必要对未来短期内光伏发电系统的出力进行预测。

针对气象数据和光伏发电出力数据之间存在随机性和非线性的特征，本文提出一种基于核偏最小二乘(KPLS)的光伏发电出力预测方法。KPLS在过程监控和系统建模领域应用较多，同时也为光伏发电出力预测的实现提供了一种可行方法。本文首先对气象数据和出力数据的特征进行分析，然后建立一种基于KPLS的预测模型，最后通过实际光伏电站运行数据进行预测。

2 气象因素与光伏发电出力

在光伏发电出力预测中，气象因素起着重要的作用。下面用统计学的方法对发电数据和气象数据的相关性以及输入输出之间的非线性关系进行分析。

2.1 气象因素与出力相关性分析

现以位于澳大利亚东海岸的容量为433 kWp的光伏阵列在2015年3月21日的发电情况进行分析说明，当天的气象信息包括环境温度、湿度、辐射值、风速、和风向五项指标数据。采用如下的相关系数计算公式来计算气象因素与发电出力之间的相关性：

各变量之间的相关性计算结果见表1。从表1可以看出，不但各气象变量与光伏出力之间存在一定的相关性，而且气象变量之间也存在着相关性。其中，光伏发电功率与太阳的辐射值相关性最大，为0.923，其次就是与环境温度的相关性也较大，为0.731，它们之间的实时曲线见图1、图2。此外，从表1中还可以看出，发电功率与环境湿度成反比，说明环境湿度越大，发电功率越小。

表1 气象因素与发电功率相关性分析结果

图1 光伏发电功率与辐射的关系

图2 光伏发电功率与温度的关系

2.2 输入输出非线性关系分析

在光伏发电系统中，环境因素为输入变量，而发电功率为输出变量，建模的目的是为了准确地描述输入输出变量之间的关系。为了说明发电功率与环境变量之间的关系，图3中分别画出了温度、湿度和辐射与发电功率的对应关系。如果两个变量之间是线性关系，那么图中所有点将会分布在一条直线上，因此从图中可以看出，只有辐射与发电功率的线性关系较强，而温度和湿度与发电功率之间的关系则呈现出较强的非线性。因此，各个环境变量与发电功率之间或多或少存在着非线性关系，为了建立准确的模型来对发电出力进行预测，就需要采用非线性的方法来处理此种数据。

3 KPLS算法

KPLS方法是一种用来处理非线性问题的非线性PLS方法，它是基于PLS的一种改进算法，因此接下来首先对基本的PLS算法作简单的介绍。

图3 输入输出变量之间的关系

3.1 PLS

偏最小二乘(PLS)算法是一种多变量线性回归算法，它的基本思想是认为系统(或过程)是被少量的隐变量所驱动，通过隐变量的形式来描述输入变量和输出变量之间的线性关系，从而建立系统的内部模型。PLS建模的目的是通过隐变量的形式来描述输入变量和输出变量之间的线性关系。假设输入数据矩阵和输出数据矩阵分别为X∈Rn×m和Y∈Rn×p，其中，n、m和p分别表示样本数量、输入变量个数和输出变量个数。PLS算法通过对X和Y进行线性分解建立如下回归模型：

式中：T＝[t1,t2,…,tA]和U＝[u1,u2,…,uA]分别是矩阵X和Y的得分矩阵；ti和ui即为隐变量；A表示保留的隐变量的个数；同时P＝[p1,p2,…,pA]和Q＝[p1,p2,…,pA]分别是X和Y的负载矩阵；E和F表示分解后的残差矩阵。

3.2 KPLS

根据Cover定理，将复杂的模式分类问题非线性地投射到高维空间比投射到低维空间得到的结果是线性可分的可能性更大。因此，在高维空间里那些数据将会表现出较强的线性关系。KPLS方法就是基于该定理，通过一个简单的核函数将输入空间非线性地投影到高维特征空间，再在此特征空间构造线性PLS模型。

表2 KPLS 算法

根据KPLS算法，高维数据Φ的得分矩阵T可表示为T＝[t1,…,tA]，输出数据Y的得分矩阵U可表示为U＝[u1,…,uA](其中A是保留的隐变量的个数)。

4 基于KPLS的预测模型

由于光伏出力受外界多个变量影响，具有强非线性和不确定性，难以建立精确的数学模型，故本文采用基于KPLS的方法进行建模，该方法无须建立光伏发电系统的内在数学模型，只要对历史数据进行处理，确定输入输出变量之间的关系即可完成光伏出力的预测。在进行光伏发电出力预测时，建立预测模型所采用训练数据为光伏监控系统数据库中的历史发电数据和气象数据。在对历史数据进行KPLS算法处理后，可以得到训练数据的得分矩阵T和U，则对于训练样本，它的拟合公式为：

而在进行预测时，对于新样本数据，它的拟合公式为：

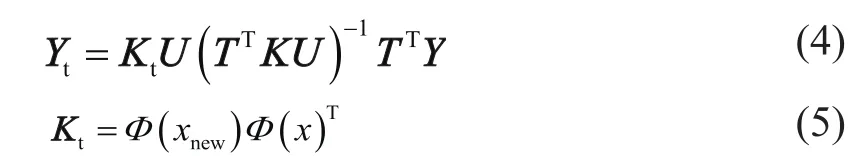
式中：xnew为新采样的数据；x为输入训练数据；

Y为输出训练数据；Kt为新数据对应的核

矩阵；Yt为预测结果。

为了说明不同模型的预测能力，通常有多种方法来衡量，本文采用均方根误差(RMSE)来评估模型对于数据的平均偏离水平，均方根误差的表达式如下：

式中：yi是实际值；是预测值；n是样本数量。

RMSE值越小，表明预测值与实际值越接近，也说明模型有更高的预测精度。

5 实例预测结果及分析

本文利用位于澳大利亚东海岸的容量为433 kWp的光伏阵列的数据来验证模型的有效性，有效光照时间为每天的7∶00～17∶00。本实验数据和信息包括该光伏阵列2015年3月21日、22日和8月13日、14日的气象数据和输出功率数据，时间分辨率均为5 min，因此每天的数据包含121个样本点。实验过程中分别用3月21日和8月13日的数据作为训练样本建立模型，然后分别对3月22日和8月14日的发电出力进行预测。

为了验证基于KPLS的光伏发电出力预测方法的性能，本文将其与基于PLS和基于人工神经网络(ANN)的方法的预测结果进行比较。首先用训练样本集分别建立PLS，KPLS和ANN模型，对于PLS和KPLS算法，通过采用交叉有效性法确定它们所保留的隐变量个数分别为3和6。此外，对于KPLS算法需要确定建立映射的核函数，本文采用径向基核函数作为映射函数，其中c是由系统所决定的系数。在用三种方法分别针对两组训练样本建立6个模型后，用这些模型分别对3月22日和8月14日的测试数据进行测试，得到的预测结果见表3。

表3 不同建模方法实验结果对比

从表3中可以看出，不但在训练数据和测试数据的采集时间相近的情况下KPLS模型的预测误差最小，而且在两种数据的采集时间相差较远时KPLS模型也能获得相对于PLS模型和ANN模型来说更为精确的预测结果。用3月21日和8月13日的数据分别作为训练数据来对3月22日的光伏出力进行预测的结果见图4、图5。从这些图中也可以看出KPLS模型的预测结果更接近实际光伏发电功率，而其余两种方法的预测曲线与实际值偏离较大。这些实验结果说明了在进行光伏出力预测时，KPLS方法能更好地提取数据的特征，建立更加准确的模型，是一种有效的光伏出力预测方法。

此外，从表3中的结果还可以发现，用相近日期的数据进行建模来对光伏出力进行预测可以获得更加准确的结果，比如，用3月21日的数据作为训练数据来对3月22日的光伏出力进行预测比对8月14日的光伏出力进行预测的结果更加精确，同时，用8月13日的数据建模来对8月14日的光伏出力进行预测的结果比用3月21日的数据建模所得结果也要精确很多。因此，在实际应用时，可以利用相似日(与预测日具有相同天气类型的历史日)或相邻日(位于预测日之前且相连的历史日)的数据进行建模，这样就可以得到更加精确的结果，但此种方式需要提前建立多个模型，预测光伏出力时再根据当天的实际情况选用合适的模型进行预测。

6 结论

本文通过对光伏电站数据及相应天气因素相关性进行分析，针对数据之间存在非线性的问题，提出了一种基于KPLS的光伏发电出力预测方法。该方法在处理非线性问题时能够很好地建立起输入变量与输出变量之间的非线性关系，充分提取非线性系统的特征。实际光伏阵列数据的应用证明了在进行光伏发电出力预测时，KPLS有较大的优势，具有很好的预测精度，因此本文所提出的方法为光伏发电出力的预测提供了一种可供选择的有效方法。但是，对于KPLS算法，由于核函数及其参数的选择将会直接影响到映射后的特征空间，所以如何正确地选择合适的核函数和它的参数也有待进一步的研究。

图4 用3月21日的数据作为训练样本对3月22日的数据进行测试的结果

图5 用8月13日的数据作为训练样本对3月22日的数据进行测试的结果

[1] 龚莺飞，等．光伏功率预测技术[J]．电力系统自动化，2016，40(4)．

[2] 陈志宝，等．地基云图结合径向基函数人工神经网络的光伏功率超短期预测模型[J]．中国电机工程学报，2015，35(3)．

[3] 赵书强，等．基于不确定理论的光伏出力预测研究[J]．电工技术学报，2015，30(16)．

[4] ZHANG,Y． et al．Dynamical process monitoring using dynamical hierarchical kernel partial least squares[J]．Chemometrics and Intelligent Laboratory Systems，2012，118(3)．

[5] 刘吉臻，等．基于自适应多尺度核偏最小二乘的SCR烟气脱硝系统建模[J]．中国电机工程学报, 2015，35(23)．