盾构隧道断面测量数据处理方法研究

高俊强夏莹祎陈 洲

(南京工业大学测绘科学与技术学院,江苏 南京211800)

0 引 言

国内长距离隧道(洞)工程采用盾构机(TBM)开挖越来越普遍,多数为直线—缓和曲线—圆曲线—缓和曲线—直线这样的设计形式且只有几个贯通面[1]。隧道断面一般是圆形,测量常用断面仪或全站仪进行,数据处理一般按最小二乘法[2]建立拟合模型计算隧道断面的中心坐标和半径。由于拟合模型中系数矩阵主元非绝对占优,实际计算时常会遇到计算结果异常的情况,适当调整数据顺序或改变数据量又不能得到较为满意的结果,会造成在外业数据采集过程中解算异常情况下无法操作或不能进行数据处理问题。此外,针对隧道断面数据按最小二乘拟合是否合理、拟合效果如何评判,在目前测绘行业规范中均未给出明确规定或标准。

国家机械工业委员会指出,评定圆度误差的算法有4种:① 最小区域法(MZC);② 最小二乘法(LSC);③ 最小外接圆法(MCC);④ 最大内接圆法(MIC)。其中,最小区域法评定圆度误差值为最小,且具有唯一性;最小二乘圆法所评定的圆度误差值也具有唯一性,但数值不是最小;另外两种方法都是近似法[3-5]。考虑到机械零件测量与盾构隧道测量的数据同样符合偶然误差规律,仅仅是采样数据密度不同而已,因此,可以借助机械工业委员会的评定指标和方法来评定盾构圆形隧道的拼装质量。本文以最小区域法计算隧道断面中心位置和半径,并将此方法和其他3类方法进行对比分析。

1 基本知识[5-6]

1.1 圆度

圆度,即圆度误差,是指断面误差曲线上离圆心最远一点到圆心距离与离圆心最近一点到圆心距离之差。

1.2 最小二乘圆法

当断面误差曲线上各点到某一圆的距离平方和为最小时,该圆即为最小二乘圆。设曲线上某点到该圆心的最大距离为r Max,另一点到圆心的最小距离为r Min,则圆度误差为f=r Max-r Min。

1.3 最小外接圆法

最小外接圆是指包容实际断面轮廓边线时,具有半径为最小的圆,也即包容断面边线的最小圆,在误差曲线上,某点到该最小外接圆的最大距离即为圆度误差。

1.4 最大内切圆法

最大内切圆是指内切于实测断面轮廓边线,或内切于断面误差曲线,且半径为最大的圆。误差曲线上某点到该圆的最大距离即为断面的圆度误差。

1.5 最小区域法

最小区域法是用两个同心圆所组成的圆环来包容实际区域,包容时,至少应有内外交替四点与此接触,这样两同心圆半径差为最小,这个半径差即为此区域的圆度误差。

2 数学模型

假设圆在XOY平面或平行于XOY平面,圆的一般方程为:(x i-a)2+(y i-b)2=r2,测得断面n(n≥3)点,各点坐标为x i,y i(i=1,2,……,n),各点到该圆圆心的距离为r i=。

按最小二乘法构建目标函数:

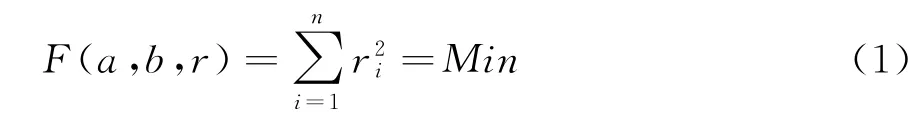
按最小区域法构建函数:

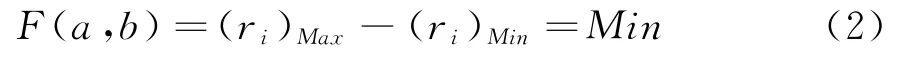
式(2)实质是求解圆心坐标(a,b)的最优问题,求解结果即是最小区域圆圆心坐标值。

同理,按最小外接圆法和最大内接圆法分别构建函数:

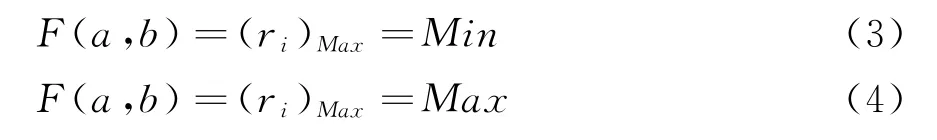
3 最小区域法的一种算法实现

最小区域的判别方法[3]是:两同心包容圆至少应与被测实际轮廓成内外相间的4点接触(图1)。

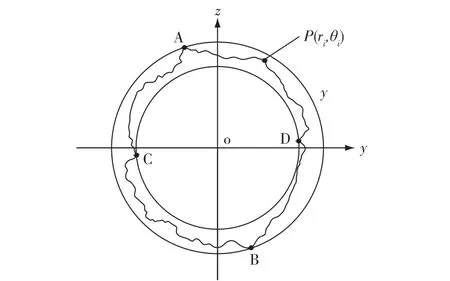
图1 最小区域法示意图

根据最小包容区域法的定义,最小包容圆与被测盾构拼装环相接触的两点之间的连线应和最大包容圆与被测盾构拼装环相接触的两点之间的连线在被测盾构拼装环内相交[7-9]。实质是根据盾构拼装环上的点找到符合要求的中心,且该中心既是最小包容圆的圆心,同时也是最大包容圆的圆心。为方便起见,不妨称最小包容圆与所测盾构拼装环相接触的点为最内点,称最大包容圆与所测盾构拼装环相接触的点为最外点。找符合要求的评定中心时,先找出两个不相临的最内点,移动中心,使两个不相临的最内点在同一圆周上;再找出和两个最内点相互间隔的两个最外点,再一次移动中心,使两个最内点和两个最外点在两个同心圆上;如果两个同心圆中一个是最小包容圆,另一个是最大包容圆,则两个同心圆的圆心即是符合要求的评定中心,否则应重新搜索。

3.1 对测量数据预处理

测量时由于控制测量、导向测量、拼装施工等误差影响,所测拼装断面的圆中心与符合要求的评定中心有一定偏离。为了能从所测数据中快速找到符合要求的评定中心,先对所测数据用面质心法进行一次预处理,计算公式如下:

假设所计算的圆心为o1,对所有点断面点进行坐标变换,得各测点以o1点为坐标原点的新坐标系下的直角坐标,极坐标,其值为:

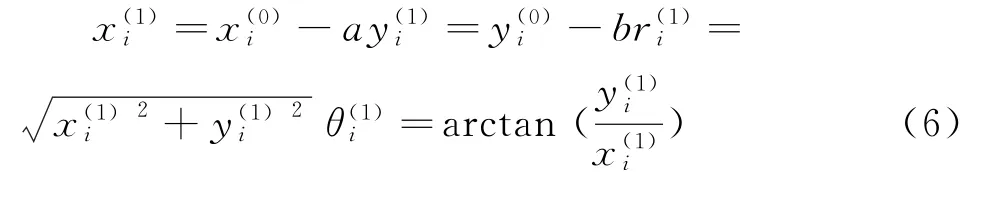
3.2 搜索理想评定中心

对上述经过加工的数据排序,找出符合条件的两最内点(图2)。设A,B是以o1为中心的两最内点,且有o1B＞o1A,将o1点沿o1B方向移动至o2点,使o2B＞o2A,o2点坐标为(x2,y2),移动距离o1o2=s,A点和B点的径向值分别为r1A和r1B,对应的方向角分别为θ1A和θ1B。由于o2B=o2A,由余弦定理知:

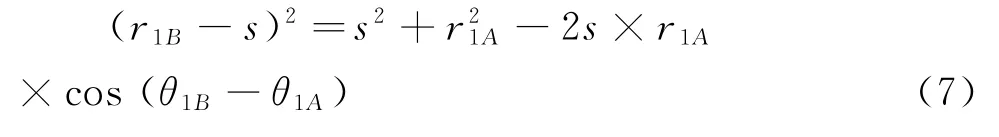
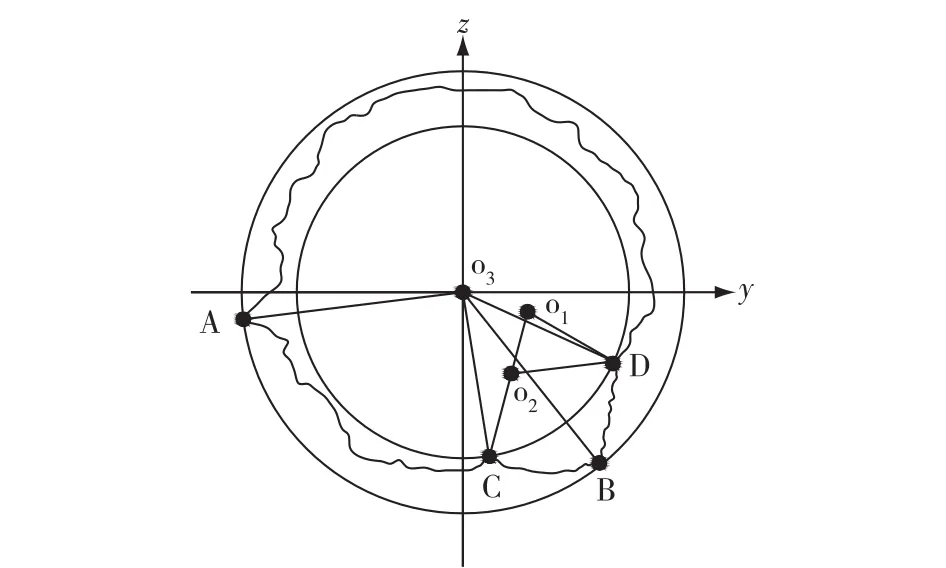
图2 最小区域圆的搜索算法

由式(7)可求得s值,从而可得o2点坐标值:

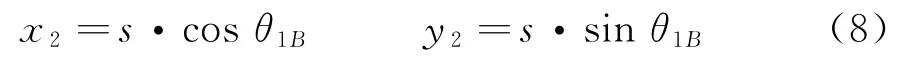
将评定中心由o1移至o2,经坐标换算,得各测点以o2点为坐标原点的新坐标系下的直角坐标和极坐标。设经过坐标变换后,A,B仍然是以o2为中心的两最内点,C,D是以o2为中心的两最外点,且满足内外点相间的条件。再次移动o2至评定中心o3(x3,y3),使o3A=o3B,o3C=o3D。按初等数学定理,为满足上述条件,o3点一定是AB和CD两中垂线的交点。设,AB的中点坐标为(x m,y m),CD的中点坐标为(x n,y n),则可求得AB的中垂线方程为:

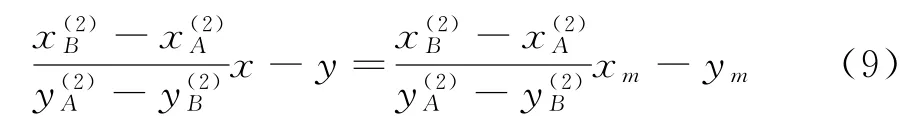
CD的中垂线方程为:

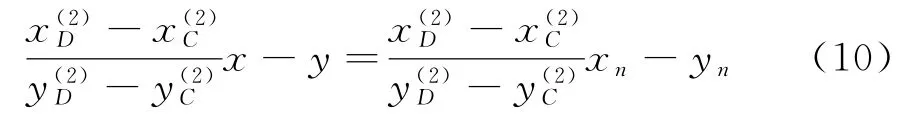
将两方程联合解算,求得o3点坐标。以o3为评定中心,判断是否满足最小区域法要求。如满足,o3点即为最小区域法的最佳评定中心,否则,应换点重复上述过程,直至找到满足最小区域法要求的理想评定中心o3为止。

最小外接圆法和最大内切圆法的计算也可通过类似方法求出[8-10]。

4 工程实例

依据上述算法编写了相应的拼装环圆度误差评定计算程序。用该程序对南京地铁一号线某段实测数据进行评定,并与其他3种方法的评定结果比较(表1)。

表1 4种不同评定方法计算结果统计表

由表1可以看出,4种圆度误差评定方法中,最小二乘法、最小区域法评定的圆心和半径以及圆度误差相差并不显著,其中最小区域法评定误差最小,和理论分析一致;而最小外接圆法和最大内切圆法对不同断面测量数据,其评定结果大小没有规律,两者明显偏大。此外,在实际拟合过程中,如果初始值选取不当,容易造成迭代计算发散。建议在在实际工作中对于每一组测量数据在生成断面数据文件后先用最小二乘法计算中心坐标,然后采用本文提出的最小区域算法,这样可取得较好效果。

5 结 语

隧道断面测量后数据处理的方法有多种,常用的是最小二乘法。本文提出最小区域法计算圆心,其误差最小,但在工程应用中计算比较麻烦。若先用最小二乘法计算出中心坐标,然后采用本文提出的最小区域算法可取得较好效果。

[1]张正禄,张松林,伍志刚,等.20～50 km超长隧道(洞)横向贯通误差允许值研究[J].测绘学报,2004,33(1),83-88.

[2]高俊强,陶建岳.利用免棱镜全站仪进行地铁隧道断面测量与计算[J].测绘通报,2005(10):41-43.

[3]国家机械工业委员会.机电一体化技术手册[M].北京:机械工业出版社,1996.

[4]国家机械工业委员会.形状与位置误差检查与测量[M].北京:机械工业出版社,1990.

[5]中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会.圆度测量 术语、定义及参数:GB/T 7234—1987[S].北京:中国计量出版社,1987.

[6]金永红,徐可伟,朱训生.基于模糊隶属函数的圆度评定参数区域法[J].计量技术,2000(4):13-17.

[7]刘玉梅,金文鹏.圆度误差评定的计算机实现方法[J].沈阳工业学院学报,1999,18(1):37-40.

[8]田社平,张守愚,李定学,等.一种用于圆度误差评价的通用算法[J].合肥工业大学学报,1996(5):10-11.

[9]谷春栋.圆度误差测量的数学模型[J].鞍山钢铁学院学报,2000(5):379-381.

[10]H.Kato.,Y Nakano and Y.,Nomura.Development of in-situ measuring system of circularity In precision cyltn[J].Japan Society of Precision Engineering,1990,24(2):130-135.