工程车辆仿生阻尼缓冲悬架特性分析
2018-03-06唐耀平陈宝明孙大刚
唐耀平,孟 杰,陈宝明,孙大刚
工程车辆作业环境恶劣,其行走机构会受到剧烈的振动冲击。传统的工程车辆悬架机构多为被动的悬架形式,该悬架仅能对振动载荷进行一定范围的缓冲,且减振效果有限。
气动人工肌肉(Pneumatic Artificial Muscle,简称PAM)是一种新型仿生气动执行机构,它由一根包裹着特殊纤维格栅网的橡胶套筒构成,通过两端与其他构件相连接(见图1a)。其工作原理是,充气后其橡胶管径向膨胀并轴向收缩,从而产生轴向拉力;而放气时则无轴向力的产生。因此,该机构是一种单向主动力输出机构。与其它主动执行机构相比,PAM具有以下特点:输出力/自重比值大(拉伸力是同直径普通气缸的10倍);结构简单,重量轻;动态特性好;无粘着、滑动现象;刚度可变、气流量小及强非线性[1-2]。
以PAM作为工程车辆仿生缓冲悬架机构,其主动力的调节具有较强的非线性和时变性,常规控制具有一定的局限性。神经网络以其对非线性函数具有任意逼近能力和自学习能力,在控制领域得到了广泛应用。本文采用智能RBF神经网络PID控制方法,对以PAM为悬架机构缓冲减振执行器的特性进行了研究。
1 仿生悬架机构的力学性质
1.1 PAM悬架模型及工作原理
履带式工程车辆通常为低速大载荷作业工况,主要承受垂直方向的冲击载荷,故在此仅考虑其垂直方向的振动;因PAM仅在充气时产生轴向收缩力,因此本文在仿生悬架机构中,采用上下2组PAM机构对拉布置形式(见图1b)。装在台车架和悬架处的传感器对二者加速度变化作实时反馈,可使上下2组PAM机构充气收缩或放气伸长。当作用在“构件2”的力向下,且“金属件”的变形量超过许用值时,上部一组PAM机构同时冲气收缩,产生阻尼(拉)力,而同时下部一组PAM机构则放气伸长。反之,当“构件2”所受力向上,且“金属件”变形量超过许用值时,下部一组PAM机构充气收缩,产生阻尼(拉)力,而上部一组PAM则放气伸长。如此,通过“构件2”起到调节上下2组PAM的动作,从而达到缓冲悬架机构的功能。
1.2 PAM力学特性
PAM具有较强的非线性、时滞特性,难以建立精确的数学模型。本文采用Wickramatunge实验模型[3],将PAM视为变刚度弹簧。PAM轴向收缩力Fe的函数关系式为

式中,k为刚度,p为充气压力,ls为伸长量,a0、a1、a2、a3为刚度k函数式中各项系数(常量,由实验获得)。
考虑橡胶套筒的弹性力作用,弹性力

2 仿生悬架模型的建立
为了便于建模,对PAM作如下假设:(1)PAM膨胀后的形状为圆柱体;(2)橡胶层厚度足够小;(3)气体流动过程为等熵绝热过程。
基于上述假设,建立起PAM悬架机构的力学模型(见图2)。图2中,m1、m2、m3分别为支重轮、构件1、构件2的质量,m4则为上部PAM悬架机构对应构件的质量;x0为地面位移,x1、x2、x3、x4分别为m1、m2、m3、m4质量体的位移;k1、k2、k3、k4分别为上述质量体对应的刚度;c1、c2、c3、c4分别为上述质量体对应的阻尼;其运动微分方程为

式中

上式中,F0为地面激励载荷,2F为一组PAM产生的主动收缩力。
3 仿生悬架的神经网络控制
3.1 控制原理
在图1中,安装在金属件处的传感器将信号传至控制器,再由控制器控制空压机,空压机对上或下部的PAM进行充气,从而起到缓冲作用(见图3)。

图2 PAM悬架模型
RBF神经网络是一种具有较强局部逼近能力、并可以任意精度逼近任意非线性函数的3层前馈神经网络。本文利用RBF神经网络对PID控制参数进行在线自整定,构造一个具有参数自整定能力、稳定的气动人工肌肉PID控制器[6-9]。对仿生悬架机构采用RBF神经网络PID控制,并采用3层3-6-1型RBF网络结构(见图3)。
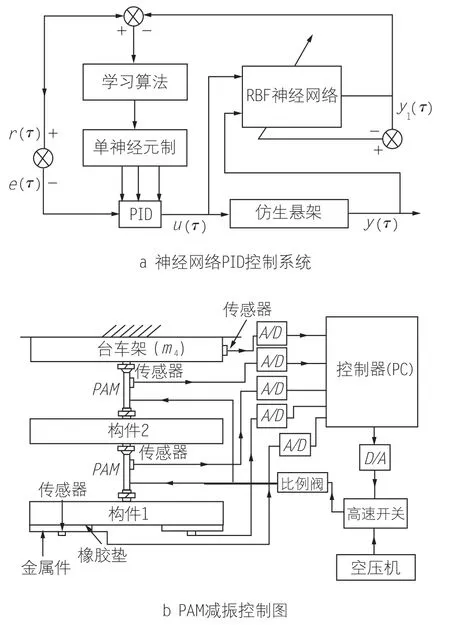
图3 仿生悬架机构控制系统
3.2 PAM的RBF神经网络控制
由于PAM具有较强的非线性,对其进行神经网络的PID控制就颇为困难。把PAM机构简化为如式(1)所示的变刚度弹簧模型,便可降低RBF神经网络PID控制的难度[3]。
仿生悬架机构的RBF神经网络PID控制过程为

式中,r为位移传感器到控制器的输入信号,y为安装在构件1下部2个传感器的输出信号(见图3),τ为采样时刻。
输入层神经元个数选为3,此时P、I、D 3项输入分别为

此处的隐层径向基采用高斯核函数

式中,Z为网络输入向量,为

bj为节点j的基宽度参数;Cj为节点j的高斯函数中心矢量,

定义辨识器的性能指标函数为

关于PID控制算法为

Kp(τ )、Ki(τ )、Kd(τ )调整采用梯度下降法
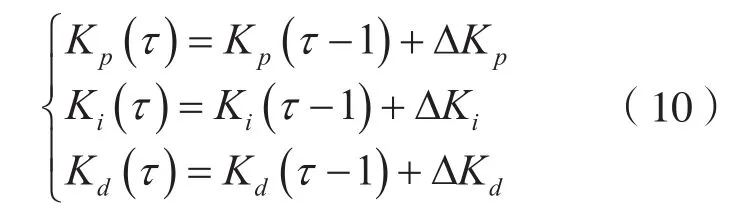
其中

式中,ηp、ηi、ηd分别为比例、积分、微分的学习速率。
引入输入误差的二次性能指标,并定义其性能指标函数为
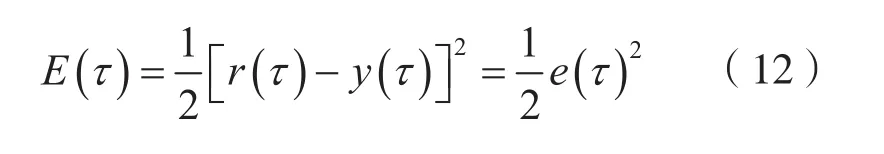
假定输入向量中

用网络辨识输出近似代替系统输出,则被控制对象的Jacobian信息可由神经网络辨识获得。

设定Kp、Ki、Kd的初始值并作实时调整,对PAM悬架的PID控制进行优化,以实现阻尼缓冲减振的功能。
4 仿生悬架的性能仿真
4.1 悬架机构参数的选择
通过对PAM仿生悬架的RBF神经网络PID的控制原理及过程的分析,编写S函数来实现Matlab/Simulink下RBF神经网络PID控制,进行仿真验证。以Festo公司的DMSP-40-100N型PAM为悬架机构的执行元件,其主要参数为:l0=0.1m,D0=0.04m,θ0=25°,最大收缩率εmax=25%,最大工作载荷为6kN;以质量为50000kg的某型号履带式工程车辆为例(其结构模型见图4),功率为300kW左右,整车高度约为4m,共有6对支重轮(每边3对),履带节距为260.35mm,支重轮的直径约为0.35m,故在底盘上有足够的空间安装文中的仿生悬架机构,将图1b中所示的仿生悬架铰接于台车架上,该机构的参数为:
m1、m2、m3、m4分别为120、200、170、7.5×103kg。
k1、k2、k3、k4分别为1.2×107、1.8×105、3.6×107、3.6×107N/m。
c1、c2、c3、c4分别为1.2×105、1.2×105、0.32×105、0.32×105N·s/m。

图4 仿真用履带式工程车辆模型示意图
仿真输入按路面激励参照GB7031-87《车辆振动输入——路面平度表示方法》。选择C、E、G级路面代表工程车辆的作业路况。取车速:1.8km/h、5.4km/h和18km/h分别代表车辆大载荷、中等载荷、空载3种工况。图5显示了安装PAM前后悬架机构所对应构件的加速度及位移的仿真曲线,其特征参数如表1所示。
4.2 仿真结果
观察图5中a、b、c和表1,发现在选定的3种工况下,PAM悬架机构与传统悬架机构相比,其垂直方向加速度有以下结果:

表1 曲线特征值
加速度最大幅值分别下降了64.5%、70.5%、65.53%;最小幅值分别下降了58.1%、50%、40%;标准差分别减小了64.4%、70.2%、65.3%。具体对该车辆而言,在作业第2挡,所受冲击最大幅值被衰减掉70%以上,其它2挡的冲击也下降60%以上,可见缓冲效果十分明显。
再观察图5中d、e、f和表1,二悬架机构垂直方向位移又有以下结果:
位移最大幅值分别下降了23.4%、18.8%、26.9%;最小幅值分别下降了46.7%、49.7%、46.7%;标准差分别减小了25.9%、23.47%、28.69%。这些数据显示,在第3挡时车身位移最大幅值衰减达到26.9%的最大值。这表明该车辆以高速挡行驶时的舒适性更好些。
由上述仿真结果可知,PAM悬架对车辆加速度的阻尼衰减度大于位移阻尼衰减度,这或许是PAM其它一些未知的因数,对其还需开展进一步的研究。

图5 安装及未安装PAM悬架对应构件加速度和位移
5 结论
(1)仿真结果表明,PAM仿生悬架机构对履带式工程车辆可起到有效的阻尼缓冲作用。
(2)PAM机构具有结构简单、重量轻、动态响应和柔顺性好的特点,可作为新型仿生悬架的缓冲执行器。
[1] Anh H P H,Ahn K K. Identification of pneumatic artificial muscle manipulators by a MGA-basednonlinear NARX fuzzy model[J]. Mechatronics,2009,19(1):106–133.
[2] Wickramatunge K C,Leephakpreeda T. Study on mechanical behaviors of pneumatic artificial muscle[J]. International journal of engineering science,2010,48(2):188-200.
[3] Wickramatunge K. C.,Leephakpreeda T. Empirical modeling of pneumatic artificial muscle[J]. Lecture notes in engineering and computer science,2009,2175(1).DOI.
[4] 任碧诗,施光林. 气动人工肌肉并联驱动平台的模糊PID控制[C]. 第六届全国流体传动与控制学术会议,2010.
[5] 杨钢,李宝仁,傅晓云.气动人工肌肉系统动态特性研究[J]. 中国机械工程,2006,17(12):1294–1298.
[6] 朱笑丛,陶国良. 气动人工肌肉伺服平台的建模[J]. 浙江大学学报(工学报),2004,38(4):1056–1060.
[7] 陶国良,谢建,周洪. 气动人工肌肉的发展趋势与研究现状[J]. 机械工程学报,2009,45(10):75–83.
[8] 王春华,唐焱. 车辆主动悬架的BP神经网络自适应PID控制[J]. 计算机仿真,2009,26(5):274–277.
[9] 焦竹青. 基于RBF神经网络的多变量系统PID解耦控制仿真[J]. 系统仿真学报,2008,20(3).
[10] Song Y,Sun D G,Zhang X,et al. Dynamic modeling study on contact-type viscoelastic suspensions used in crawler construction vehicles[J]. Mechanics based design of structures and machines,2009,37(4):513- 537.
[11] Psarros D,Papadimitriou V,Chatzakos P,et al.A service robot for subsea flexible risers[J]. IEEE robotics and automation magazine,2010,17(1):55-63.
[12] Mitsuota M,Inaba S,Inoue E,et al. Dynamic model of an agricultural rubber crawler vehicle with nonlinear spring(Part 1)-Investigation of the nonlinear interaction between a track roller and an agricultural rubber crawler[J]. J Japanese society of agricultural machinery,2008,70(5):48-54.
[13] Mitsuota M,Inaba S,Inoue E,et al. Prediction and evaluation of vibration characteristics of an agricultural rubber crawler vehicle equipped with movable track rollers[J]. J. Japanese society of agricultural machinery,2008,70(5):41-47.
