用于微型飞行器的高转速超声电机

王 乐， 王永杰， 芦小龙， 赵淳生

(1.南京航空航天大学机械结构力学及控制国家重点实验室 南京, 210016)(2.黔南民族师范学院数学与统计学院 都匀, 558000)

引 言

微型飞行器(micro air vehicles)具有结构紧凑、体积小、质量轻和便于携带等优点，可以实现低空或近距离的侦察和监视的功能，并且能够承担通信中继和电子对抗等任务，在军事和民用领域有着广阔的应用前景，是目前国际上航空器研究的热点[1-5]。按照飞行方式,微型飞行器可分为固定翼微型飞行器、扑翼微型飞行器和旋翼微型飞行器[6]。微型飞行器设计是一个多学科交叉的研究领域，其中一个关键设计环节是驱动机构的设计。针对旋翼微型飞行器，现有的驱动机构通常利用无刷电机或空心杯电机，由于抗电磁干扰问题，限制了现有微型飞行器的应用环境。伴随着智能材料性能的提升，基于非电磁作动机理的新一代先进作动器发展迅速，在航空航天、光学、生物医疗和微机电系统等领域表现出特有的优势，为微型飞行器的驱动机构提供了新的设计思路。以行波型超声电机(TRUMs)为例，其工作原理是利用压电材料的逆压电效应，激发弹性体(定子)在超声频率声段内微幅的振动，继而通过定子与转子之间的摩擦驱使转子旋转，实现电能与机械能的转换[7-10]。基于其结构紧凑、转矩密度大、断电自锁、位移分辨率高和无电磁干扰等优点超声电机已经成功应用于细胞穿刺、集成电路生产和光纤对焦等多种场合。由于现有超声电机的转速普遍不高，尚且不能作为驱动机构直接应用于旋翼微型飞行器。目前，高转速超声电机的研究分为非接触式和接触式两种。文献[11-12]研制的非接触式超声电机可以达到4 400 r/min。Ji等[13]设计的非接触式超声电机转速可以达到6 031 r/min，但由于非接触超声电机比接触式超声电机结构较复杂、体积较大、输出力矩较小，不适用于微型飞行器领域。Borodinas等[14]设计的接触式超声电机最高转速可以达到3 850 r/min，其结构简单、重量轻、体积小，为微小型超声电机在微型飞行器领域内的应用奠定了基础。

针对基于智能材料的特种微型飞行器的研制需求，笔者提出了一种新型接触式高转速超声电机。首先，根据微型飞行器的使用需求开展电机的结构设计，在此基础上分析该电机的驱动原理；其次，建立电机的有限元模型，确定工作模态，并分析定子的振幅与定子关键尺寸之间的关系；然后，对样机的机械特性进行试验，测试样机的振动特性、输出特性和最高转速；最后，对安装旋翼后的输出升力进行测量。相关研究方法为进一步研制超声电机作为微小飞行器的直接驱动机构提供了支撑。

1 电机工作原理

1.1 结构及驱动原理

图1(a)为电机的主体结构，包括基板、压电陶瓷片、转子、碳纤维管、锥形扣件、弹簧和卡环。其中，基板和碳纤维管组成定子的主体结构，基板外金属环(∅30 mm×∅22 mm×0.5 mm)与内金属环(∅20 mm×∅4 mm×1 mm)通过4根金属连接足连为一体。碳纤维管固定在基板中心，转子通过锥形扣件、弹簧、卡环装配在碳纤维管上，预压力使得锥形扣件、转子与碳纤维管上下两端的锥面紧密接触，施加的预压力可以通过改变卡环的位置进行微调。陶瓷片沿厚度方向极化，其中4个分区分为两相，相对的两个陶瓷片为一相，极化方向反向安置，用于激发定子基板的一阶面外弯曲振动模态。两相压电陶瓷分别施加相位差为90°的同频率、等幅交流激励信号，通过压电陶瓷的逆压电效应，可以分别激发出空间上和时间上相位差为π/2的面外弯曲振动模态，并且幅值相等。这两个振动模态相互耦合，在定子基板上叠加形成行波。定子基板的面外弯曲振动模态与碳纤维管垂直于基板的弯振模态相耦合，使得基板的行波运动经过碳纤维管进一步放大，进而通过摩擦作用驱动转子做高速旋转运动。以往的微型旋转超声电机通常采用定子基体直接驱动转子运动的方式[15-17]，为获得更高的转速，需要增加压电陶瓷的数量和体积，这将导致电机定子的尺寸和重量的增加。笔者所设计的超声电机基于多模态耦合技术，作为电机关键部件的碳纤维管在有效放大振幅的同时，实现了压电陶瓷激励单元到定子接触端面的过渡。与传统的微型超声电机相比，笔者研究的电机采用的多模态耦合方式能够更加有效地提高提高定子的振幅。此外，该电机不需要专门设计夹持机构，可以直接作为驱动机构应用，这种结构有利于散热、减轻电机重量，并且提高了电机工作的稳定性。

1.2 激励方式

压电陶瓷选用环状PZT-8功率型压电陶瓷(∅20 mm×∅8 mm×0.2 mm)，极化方向和接线方式如图1(b)所示。当A相输入正弦信号，B相输入余弦信号，可以激发出碳纤维管驱动端面质点在空间中做椭圆运动轨迹，并通过摩擦作用驱动转子做顺时针旋转运动，当施加信号相差-π/2相位差时电机转子可以实现反转做逆时针旋转运动。上下两面陶瓷极化方向和加电方式完全一致。

图1 电机结构及驱动方式Fig.1 Configuration of the ultrasonic motor

2 电机有限元建模与模态分析

通过有限元分析可以计算定子的固有振型、模态频率，计算出碳纤维管长度的最优值和计算出了定子驱动端面质点的运动轨迹。电机的基本动力学方程可通过最小势能原理导出，其表达式[18-19]为

(1)

其中：M,K,T,S和C分别为压电振子有限元模型的质量矩阵、刚度矩阵、电致弹性矩阵、电容矩阵和阻尼矩阵;u,φ,F和Q分别为节点位移向量、电势向量、外力向量和电极上分布的电荷向量。

通过式(1)可以计算出不同激励电压下电机定子与转子接触点的位移。

笔者设计的电机定子弹性体采用的是钛合金材料(TC4)，碳纤维管材料为T400HB，压电陶瓷片为PZT-8。定子组件的材料参数如表1所示。压电陶瓷材料的相关参数如表2所示。

表1 定子组件材料力学参数Tab.1 The mechanical properties of the stator materials

表2 压电陶瓷材料性能Tab.2 Properties of the PZT used in the motor

碳纤维管的高度值初始设定为10 mm，确定好定子及组件材料的参数后，利用有限元软件Ansys 15.0三维建模软件对电机定子进行三维建模。其中边界条件为：外金属环表面为固定面，定子组件整体的有限元模型如图2所示，整体模型有8 715个单元，24 022个节点。最终得到的是两相激励信号都为100Vp-p的情况下，定子的工作模态如图3所示，对应的模态频率为29.9 kHz。为找出碳纤维管的最佳高度，将碳纤维管的高度逐次增加1 mm直到20 mm，对应每次的碳纤维管高度逐次做谐响应计算，对比相应的计算结果，从中找出所需要振幅最大的高度方案。最终得到的碳纤维管最优高度为16 mm。图4为激励信号100 Vp-p时，碳纤维管高度与碳纤维管驱动端面质点振幅的关系。当碳纤维管高度分别取11，12，13和20 mm时，无法得到需要的工作模态。可以看出，在碳纤维管高度为16 mm时，振幅最大。

图2 定子组件有限元模型Fig.2 The finite element model of the stator

图3 定子的工作模式分析Fig.3 Vibration mode of the stator

碳纤维管具有放大定子基板振幅的作用，为了更加直观地体现碳纤维管驱动端面的运动，取驱动端面一个质点p(位置如图3所示)，在一个周期内多个不同时刻对质点的运动轨迹进行仿真，根据计算结果绘制碳纤维管顶端驱动面质点的三维运动轨迹(如图5所示)。可以看出，质点在三维空间中的运动轨迹为椭圆轨迹，且与xOz平面有一定夹角。

图4 碳纤维管高度与定子振幅关系曲线Fig.4 Relationship between height of carbon fiber tube and amplitude of the stator

图5 定子驱动端面质点的三维运动轨迹Fig.5 Calculated moving trajectory of one selected point on driving surface

3 实验结果和讨论

基于优化后的电机结构尺寸参数制造了电机样机，如图6所示。电机外围尺寸为∅30 mm×26 mm，质量为3g。

图6 电机样机Fig.6 Image of the prototype ultrasonic motor

利用激光多普勒测振仪(PSV-300F-B)对电机定子进行了扫频实验，得到了定子的振动频率和振幅。实验时电机的驱动电压为100 Vp-p。实验得到电机定子的频率响应曲线如图7所示，电机实际工作的共振频率为30.9 kHz，与理论计算值29.9 kHz相比上升了1.0 kHz，分析电机实际工作的共振频率与理论值的不一致的原因，可能存在于：a.理论建模中的误差；b.仿真计算过程中定子结构的等效与简化。定子的振型图如图8所示，当激励电压为100 Vp-p时，测得的振幅为1.2 μm，定子的振型图表明定子实测的振动模态和通过有限元仿真结果基本一致。

图7 电机定子频率响应曲线Fig.7 Frequency response of the stator

图8 电机定子振型图Fig.8 Vibration pattern of the stator

为了测量电机转速，在样机转子上贴上反光标记并通过光电式非接触激光测速仪(SW826)进行测量。实验过程中，通过卡环调整好电机转子与定子之间的预压力，在压电陶瓷的两相分别输入相位差为π/2的正弦交流信号，电压为150 Vp-p。经实验发现，电机在驱动频率为30.9 kHz附近时具有稳定的工作特性。因此，在该频率下研究电机输出空载转速随驱动电压的变化规律，实验结果如图9所示。可以看出，在驱动频率一定的情况下，电机转速与输入电压峰值基本呈线性关系，当电压增加到350 Vp-p时，电机最高转速可达5 520 r/min。

电机空载转速随驱动频率的变化关系如图10所示，激励电压维持在150 Vp-p。可以发现，该曲线与结构在共振频带内的幅频特性类似，这是由于电机工作在共振频率附近，其输出速度随振动幅值的增大而增加，当驱动频率为30.9 kHz时，电机最大转速可达到3 020 r/min。

电机的启动特性如图11所示。施加的激励信号频率为30.9 kHz，电压为150 Vp-p。当二者相位差为π/2时，电机转子做顺时针旋转运动，当施加信号相位差为-π/2时，电机转子逆时针旋转运动;从启动到电机稳定工作所需时间在25 ms左右。

图9 驱动频率为30.9 kHz时电压-转速曲线图Fig.9 Relationship between the output performance and the voltage at 30.9 kHz

图10 驱动频率为150 Vp-p时频率-转速曲线图Fig.10 Relationship between the output performance and the frequency at 150 Vp-p voltage

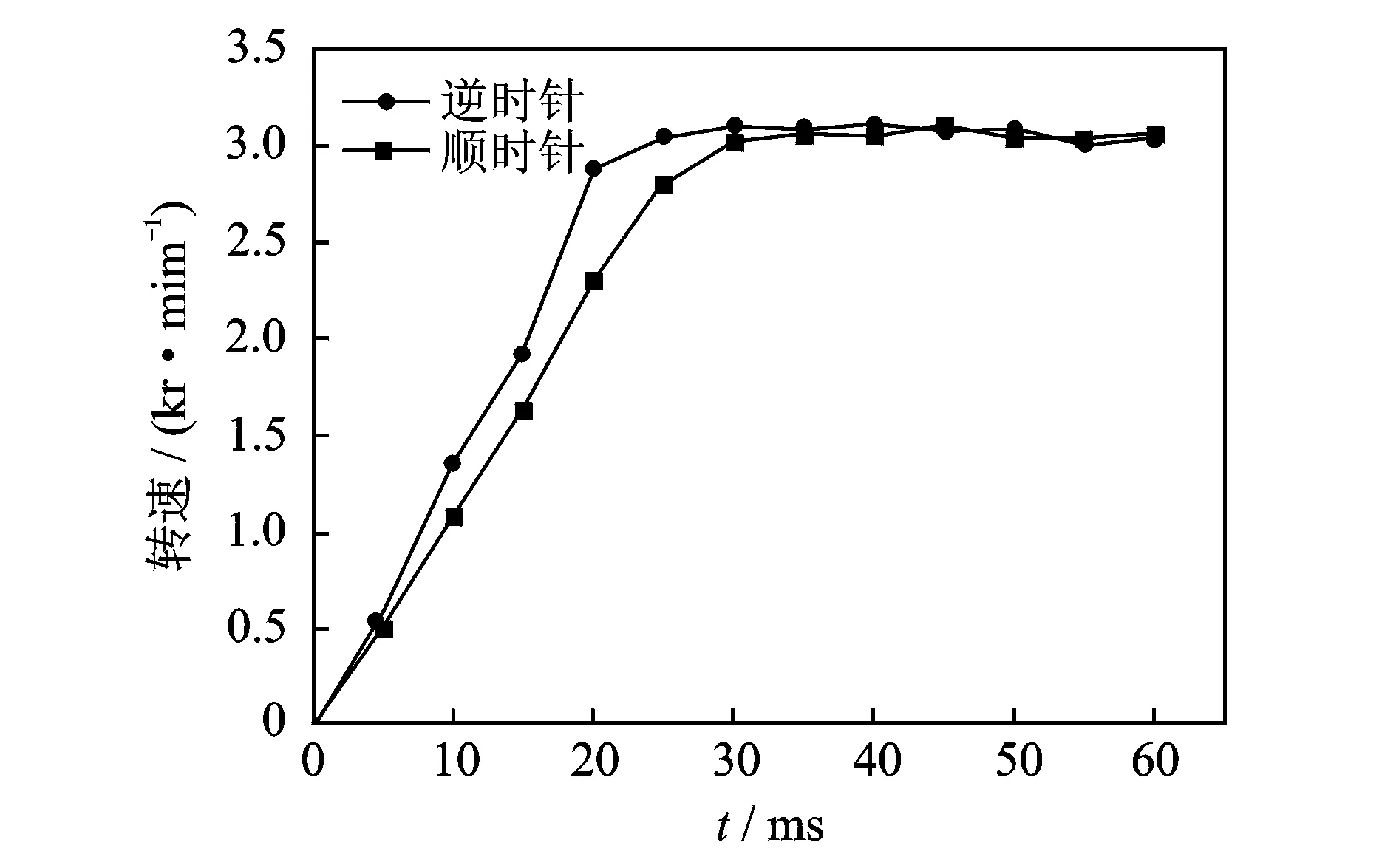
图11 驱动频率为30.9 kHz,驱动电压为150Vp-p 时正/反转速与工作时间的关系(启动特性)Fig.11 Relationship between the output performance and the operating time at 150 Vp-p voltage and 30.9 kHz

将旋翼直接固连在电机转子输出轴上，参考文献[20-22]中的实验方法，利用一台梅特勒-托利多(AL204)高精度天平测试电机驱动旋翼时的升力。为测试电机驱动旋翼旋转产生的升力随旋翼转速变化的规律，将电机驱动频率设定在30.9 kHz，电机驱动电压由100 Vp-p逐渐增大到200 Vp-p，测试结果如图12所示。可以看出，旋翼产生的升力与电机转速基本呈线性关系，旋翼转速最大可达到2 800 r/min，产生的最大升力值在14 mN左右。

图12 驱动频率为30.9 kHz时升力-转速曲线图Fig.12 Relationship between the rotor lift force and the rotary speed at 30.9 kHz

4 结 论

1) 针对超声电机在微型旋翼飞行器中的应用问题，从电机的驱动原理到电机尺寸优化及有限元计算做了系统阐述。

2) 对样机进行了扫频实验，实验结果验证了工作原理的可行性。

3) 对样机进行了机械特性测试实验，并对电机装上旋翼后工作时升力进行了测试实验，为下一阶段超声电机作为微型无人机的直接驱动机构奠定了一定的基础。

[1] Wilson J R. Mini technologies for major impact[J]. Aerospace America, 1998,36(5):36-42.

[3] Hu H, Kumar A G, Abate G, et al. An experimental investigation on the aerodynamic performances of flexible membrane wings in flapping flight[J]. Aerospace Science & Technology, 2010,14(8):575-586.

[4] 陈国栋, 贾培发, 刘艳. 微型飞行器的研究与发展[J]. 机器人技术与应用, 2006(2):34-44.

Chen Guodong, Jia Peifa, Liu Yan. Research and development of MAV [J]. Robot Technique and Application, 2006(2):34-44. (in Chinese)

[5] 崔秀敏, 王维军, 方振平. 小型无人机发展现状及其相关问题分析[J].飞行力学, 2005, 23(1):14-18.

Cui Xiumin, Wang Weijun, Fang Zhenping. Present situation and some problems analysis of small-size unmanned air vehicles[J]. Flight Dynamics, 2005,23(1):14-18. (in Chinese)

[6] 于雅楠. 微型旋翼飞行体自适应气动外形抗扰动特性研究[D]. 天津：天津大学, 2012.

[7] 赵淳生. 超声电机技术与应用[M]. 北京：科学出版社, 2010:162-163.

[8] Lu Xiaolong, Hu Junhui, Yang Lin, et al. A novel dual stator-ring rotary ultrasonic motor[J]. Sensors & Actuators A Physical, 2013,189(2):504-511.

[9] Fujimura T, Funakubo T, Imabayashi H, et al. Ultrasonic motor: US, 5416375[P]. 1994-10-18.

[10] Lu Xiaolong, Hu Junhui, Yang Lin, et al. A novel in-plane mode rotary ultrasonic motor[J]. Chinese Journal of Aeronautics, 2014,27(2):420-424.

[11] Hu Junhui, Yamazaki T, Nakamura K, et al. Analyses of an ultrasonic motor driving fluid directly[J]. Japanese Journal of Applied Physics, 1995,34(5):2702-2706.

[12] Yamazaki T. Trial construction of a non-contact ultrasonic motor with an ultrasonically levitated rotor[J]. Japanese Journal of Applied Physics, 1996,35(5):3286-3288.

[13] Ji Ye, Zhao Chunsheng. A new type non-contact ultrasonic motor with higher revolution speed[J]. Piezoelectrics & Acoustooptics, 2006,28(5):523-527.

[14] Borodinas S, Vasiljev P, Mazeika D. The optimization of a symmetrical coplanar trimorph piezoelectric actuator [J]. Sensors & Actuators A Physical, 2012, 200(10):133-137.

[15] Tao Ye, Zhao Guiwen, Zhang Weiping, et al. Combustion synthesis and photoluminescence of nanocrystalline Y2O3 : Eu phosphors[J]. Materials Research Bulletin, 1997,32(5):501-506.

[16] Dong Zhaopeng, Yang Ming, Chen Zhangqi, et al. Design and performance analysis of a rotary traveling wave ultrasonic motor with double vibrators[J]. Ultrasonics, 2016,71(11):134-141.

[17] Zhao Yanqiang, Yuan Songmei, Chu Xiangcheng, et al. Ultrasonic micro-motor with multilayer piezoelectric ceramic and chamfered driving tips[J]. Review of Scientific Instruments, 2016,87(9):291-300.

[18] Frangi A, Corigliano A, Binci M, et al. Finite element modelling of a rotating piezoelectric ultrasonic motor[J]. Ultrasonics, 2005,43(9):747.

[19] Tzou H S. Piezoelectric shells-distributed sensing and control of continua[M]. Boston: Kluwer Academic, 1993:100-102.

[20] 孙柴成, 徐玉, 谭中华, 等. 四旋翼无人飞行器驱动系统设计与性能测试[J]. 机电工程, 2014,31(12):1648-1652.

Sun Chaicheng, Xu Yu, Tan Zhonghua, et al. Design and performance evaluation of quadrotor drive system[J]. Mechanical & Electrical Engineering Magazine, 2014,31(12):1648-1652. (in Chinese)

[21] 朱清华. 自转旋翼飞行器总体设计关键技术研究[D]. 南京:南京航空航天大学, 2007.

[22] 高正，陈仁良. 直升机飞行动力学[M]. 北京：科学出版社, 2003:24-28.