改进小波去噪-Teager算子的齿轮微弱故障提取方法

何 巍, 袁 亮, 章翔峰

(新疆大学机械工程学院 乌鲁木齐,830047)

引 言

齿轮箱是机械传动中的重要组成部分,在齿轮箱的失效故障中,齿轮的故障占据了很大比重,研究齿轮箱的状态监测以及故障诊断技术,对于保障机械设备的稳定运行具有重要意义[1]。齿轮箱故障在早期阶段具有特征信息弱的特点,致使故障特征不易被识别[2]。对于齿轮的故障研究,能够有效准确地提取故障特征是进行齿轮箱故障诊断的关键[3]。齿轮箱发生故障时,其振动信号通常是非平稳信号[4]。近年来,在齿轮箱的故障诊断研究中,齿轮箱的微弱故障信号不单是多种信号的叠加,可能是多种故障因素耦合、多种信号调制的结果[5]。在故障信号处理方面,程军圣等[6]提出了基于经验模态分解(empirical mode decomposition,简称EMD)的能量算子解调方法,通过提取解调后的调幅调频信号的幅频信息进行故障诊断。李辉等[7]提出基于EMD与Teager能量算子解调相结合的方法,识别出齿轮箱轴承的故障。张德祥等[8]将EMD与Teager能量谱应用到齿轮箱振动信号分析中,验证了Teager能量特征表达在故障特征提取中的可行性。经验模态分解方法能够实现对信号的解调,但其抗模态混叠能力不足,为此集合经验模态分解的提出一定程度上弥补了EMD模态混叠的不足[9-11]。李辉等[12]将EEMD方法和Teager-Huang变换结合,并将其运用到齿轮故障诊断中。由于齿轮传动过程中齿轮的微弱故障振动信号易被现场较强的随机噪声干扰,造成EEMD分解精度不高,从而导致信号的故障特征并不明显。另外，对信号进行EEMD分解需要进行多次EMD分解,当信号中含有噪声时会导致EEMD计算效率不高。因此,对原始信号进行去噪处理能够减少EMD的运算时间,通过去噪处理能够减少边界效应造成的累计误差。同时,由于齿轮的微弱故障振动信号能量相对较低,因此有必要对信号进行信号增强。

笔者将改进小波阈值去噪与Teager能量算子方法相结合,提出一种改进小波去噪和Teager能量算子的齿轮微弱故障特征提取方法。将齿轮故障信号进行小波消噪处理,然后对消噪后的信号进行EEMD分解,并计算各IMF分量的相关系数及其频谱筛出虚假分量,对相关度高的IMF进行Teager能量算子运算增强信号中的瞬态冲击成分。

1 信号去噪处理

在实际环境中,齿轮箱的故障振动信号会由于外界环境干扰和齿轮箱自身装配等问题的影响,会导致噪声产生。在对故障信号进行处理分析时,应当首先对信号进行去噪处理[13]。信号去噪的方法较多,如形态学滤波和小波变换等。笔者通过对仿真信号分别进行一维形态学滤波处理和改进小波去噪处理,并对处理结果进行定量分析。

1.1 一维形态学滤波原理

一维形态学滤波是由数学形态学的基本运算与组合并且只针对一维振动信号进行分析的运算[14]。数学形态学运算包括腐蚀、膨胀、开启和闭合。笔者使用开-闭和闭-开级联组合形态滤波器,对仿真信号进行消噪处理。

y(n)=(f∘g·g+f·g∘g)/2

(1)

其中: ∘表示开启运算; ·表示闭合运算;f为原始信号;g为结构元素,综合考虑笔者采用三角结构元素。

1.2 改进小波阈值去噪原理

在实际工程中,振动信号的组成比较复杂,除了含有有用信息组成外,还含有高频的噪声信号[15]。小波阈值去噪的主要思想就是以某一阈值对信号小波分解后的小波系数进行处理,并对处理后的信号进行重构达到去噪的目的。小波阈值去噪处理一维信号的步骤:

1) 选定某一小波基和小波分解的层次N,然后对信号进行N层分解;

2) 选定一个合适的阈值对每一层的高频系数进行阈值过滤处理;

3) 根据处理后的结果进行小波重构。

小波阈值去噪方法根据阈值选区规则的不同，可以分为硬阈值法和软阈值法。其中：硬阈值法的阈值函数较为简单,但是会造成函数整体不连续; 软阈值法虽整体连续但是幅值较大的小波会产生衰减。针对以上不足,在软阈值法的基础上对其阈值函数进行构造。

(2)

这样可以有效避免软阈值法中对幅值较大的小波的衰减,并尽可能消除软阈值函数的恒定偏差。

1.3 仿真分析

为验证去噪算法的正确性,构造以下包含特征频率为f1=10Hz，f2=20Hz，f3=30Hz，f4=40Hz的噪声信号

(3)

其中: noise为噪声。

对含噪信号分别进行一维形态学滤波、硬阈值、软阈值和改进小波阈值去噪处理。

笔者选用db10小波基,设定分解层数为5层,对仿真信号进行去噪处理,得到的信号时域波形如图1所示。为分析不同去噪方法的去噪能力,笔者采用去噪后信号的信噪比(RSN)和均方根误差(ERMS)进行分析如表1所示,图中幅值为无量纲单位。

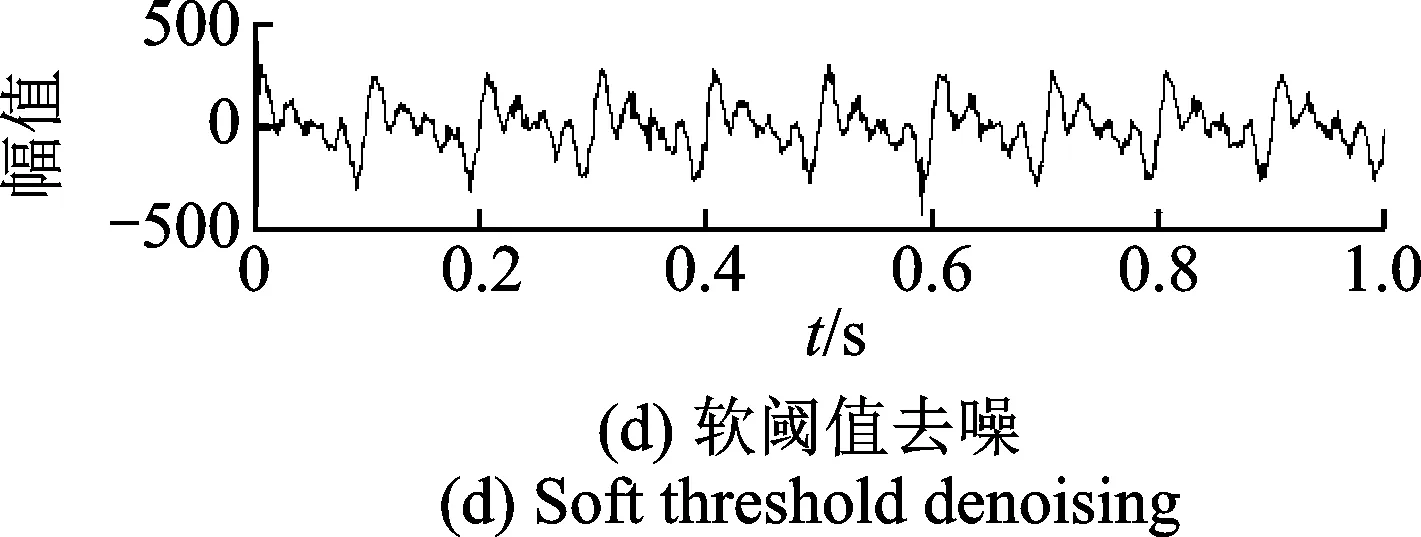
图1 仿真信号及去噪后时域波形Fig.1 The simulation signal and time domain waveform afterdenoising

表1 去噪效果Tab.1 Denoising effect

从表1可知,形态学滤波去噪效果较差,其信噪比较低且均方根误差较大,而改进小波阈值去噪后的信号其信噪比高、均方根误差低,综合得出改进阈值法具有较好的去噪效果。

2 EEMD法和Teager能量算子

2.1 EEMD原理

由于传统EMD方法容易产生模态混叠[16-17],因此Lei等[18]针对EMD方法的不足提出了EEMD方法。其原理是在原始信号的基础上加入高斯白噪声,利用其频率分布的特性使信号在不同尺度上具有连续性,并对信号进行多次均值处理,从而使信号中的噪声相互抵消,得到无模态混叠的信号分量。对于一维信号x(t)进行EEMD分解的步骤如下。

1) 在原信号x(t)中混入高斯白噪声,得到

xi(t)=x(t)+ni(t)

(4)

其中:xi(t)为第i次加噪后的信号;ni(t)为高斯白噪声,其幅值均值为0,标准差为常数。

2) 对加噪后的信号xi(t)进行EMD处理,得到多个IMF分量cij(t)以及一个余项ri(t)。cij(t)为第i次加噪后的信号经过EMD分解得到的第j个IMF分量。

3) 对步骤1和步骤2进行N次重复,得到多个IMF分量。EEMD分解的结果为

(5)

其中:cj(t)为原始信号经EEMD分解后得到的第j个本征模态分量IMF;r(t)为最终的残余分量。

根据Wu等[19]建议,为有效避免EMD模态混叠的问题,笔者设定EEMD分解中总体平均次数N值为100,高斯白噪声的标准差为原始信号标准差的0.2倍。

2.2 Teager能量算子原理

对信号进行能量解调,常用HHT提取信号的能量谱和边际谱,由于HHT需要进行复数运算,导致其运算量较大。针对这一不足，Kaiser提出一种Teager能量算子(teager energy operator,简称TEO)方法[8]。

Teager能量算子是一种非线性算子,具有无需进行复数计算和计算量小的特点,能够有效提取信号的能量。对于信号x(t),TEO定义为

(6)

离散信号x(n)的TEO定义为

ψ[x(n)]=x2(n)-x(n+1)x(n-1)

(7)

文献[8]采用Teager能量谱表示信号的能量变化,即

(8)

其中: Re表示取IMF分量和的实部。

3 齿根裂纹故障特征提取

3.1 实验参数以及装置

图2 实验设备Fig.2 Experimental equipment

实验装置为风力涡轮机动力传动故障诊断综合实验台,本算例中设定输入转速8 640°/s(1 440 r/min),负载扭矩为5×102N·mm,信号采样设备为DT9837,采样频率为10 kHz,采样时间为1 s。实验按照不同状况分组进行,实验装置如图2(a)所示。实验中,选取二级减速器的输入级齿轮进行故障诊断,在输入级齿轮上通过特种加工做出单个轮齿的单一裂纹,如图2(b)中圈内曲线所示,用来生成故障信号,故障状况与正常状况下输入转速与负载相同,二级减速器的相关参数如表2所示。

表2 齿轮参数表Tab.2 Gear parameter list

表2中，齿轮1和2为输入级,齿轮1的转频f=24 Hz,啮合频率fz=696 Hz。

3.2 信号去噪处理

当定轴齿轮传动出现故障时,其产生的振动信号中还可能与其他故障因素耦合[2]。图3为齿轮箱在两种状态下的原始信号与改进小波去噪后信号时域图谱。

图3 时域测试信号Fig.3 Time domain test signal

仅从时域信号上无法立即得出有用信息,难以直接判定测试信号是正常齿轮还是故障齿轮的。

3.3 集合经验模态分解

对去噪后的故障信号图3(d)进行EEMD分解,得到13个IMF分量和1个残余分量r,如图4所示。

信号经过集合经验模态分解后,将得到多个IMF分量,由于在分解时高斯白噪声的加入,导致分解后的IMF分量中有无用分量的产生。为筛选出有用的分量,笔者对经EEMD分解后的各个IMF分量计算相关度系数ρxy。相关度系数是统计学概念,用来描述随机变量之间的线性相关性,计算式为

(9)

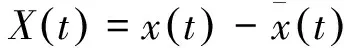
根据式(10)计算,所得结果如表3所示。从表3看出，相关系数并不是呈现递减的趋势,其中有数据跳变,因此仅凭借相关系数仍不足以判断IMF中的无用分量。为克服这一不足,笔者对IMF进行频域变换如图5所示,幅值为无量纲单位，根据图谱中是否含有故障特征的基频和倍频筛选有用分量。

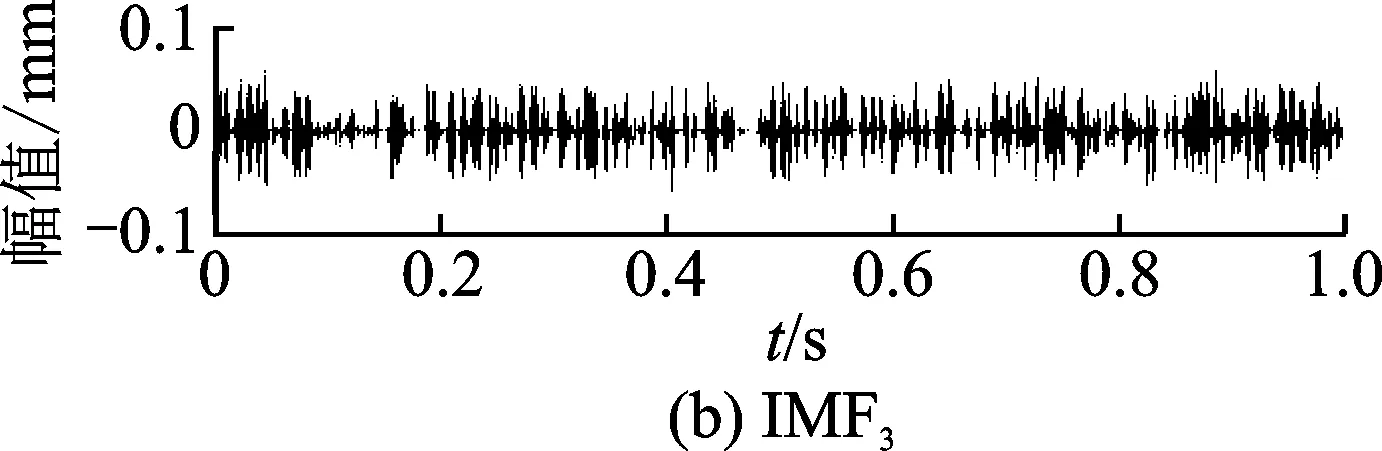
图4 齿轮箱故障信号EEMD分解结果Fig.4 EEMD decomposition results of fault signal of gearbox

表3 各IMF以及残余分量的相关系数Tab.3 The correlation of IMFs and residual

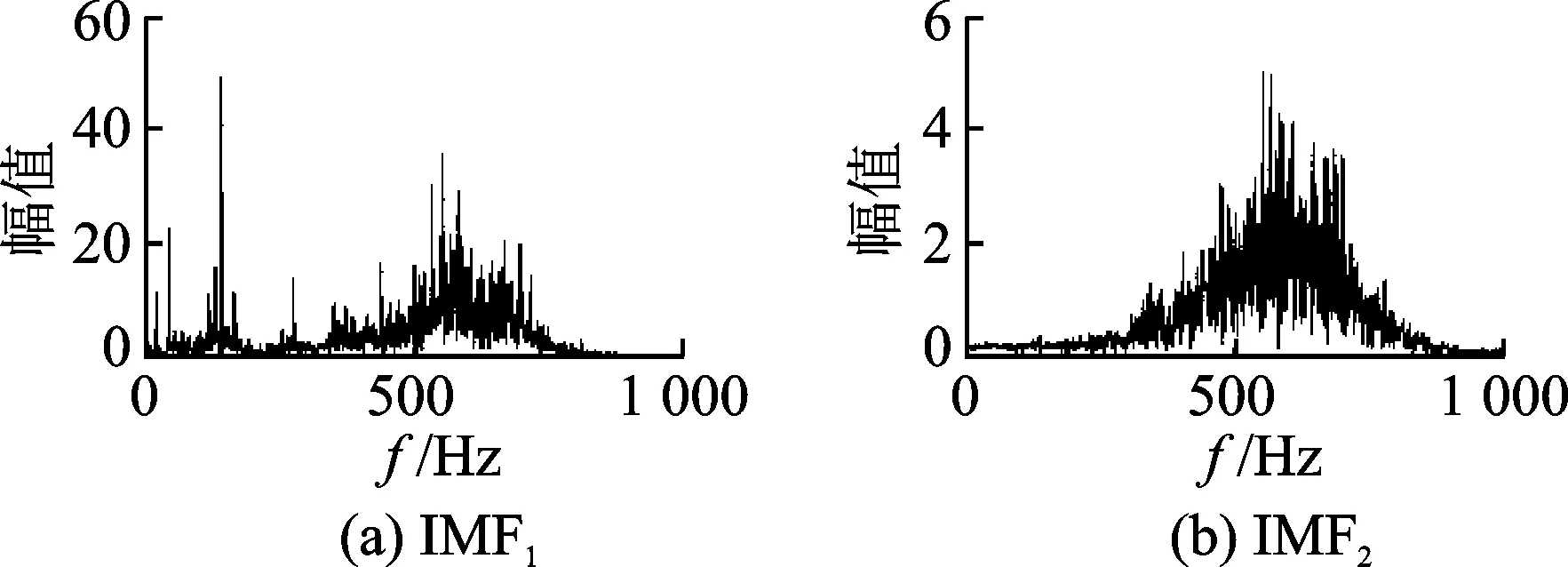
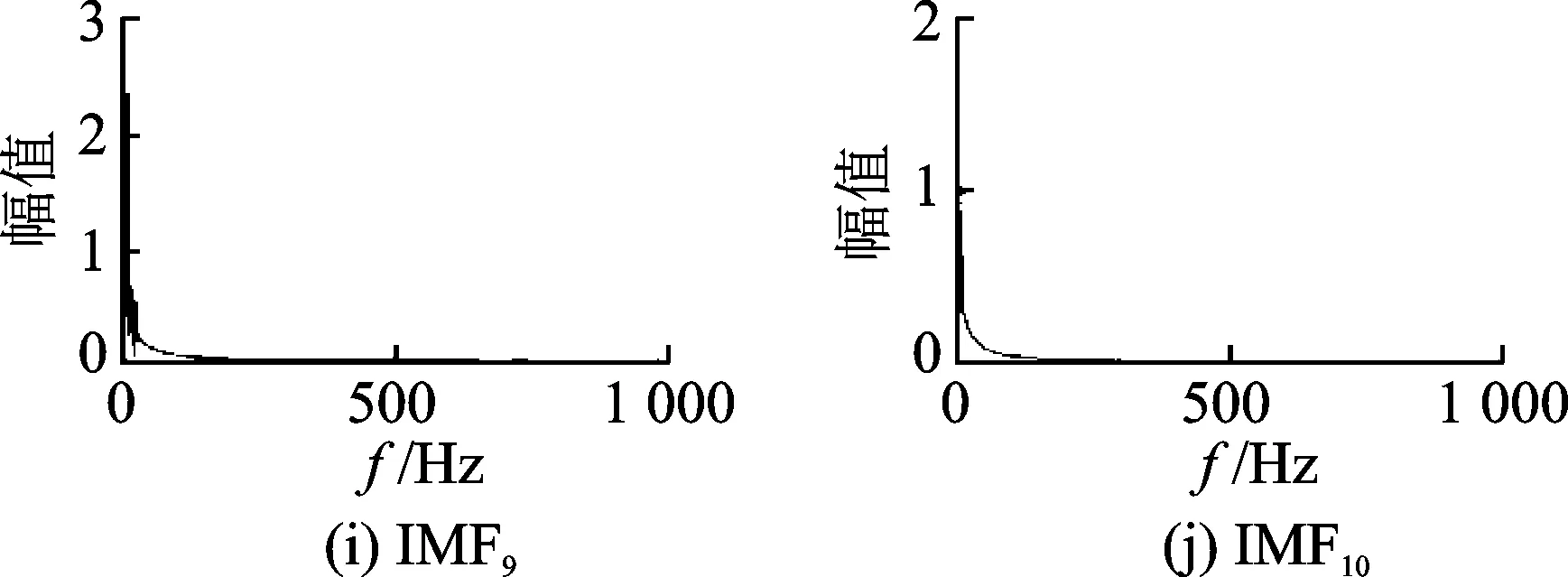
图5 各IMF的频谱Fig.5 IMFs frequency spectrum

求取EEMD分解后的前10个IMF的频谱后,可以发现第1个到第8个中含有故障齿轮的基频以及倍频,应该保留前8个IMF分量进行信号重构,从第9个IMF以后,并不包含有效频率成分,应当剔除从第9个之后的无用IMF分量。

3.4 Teager能量算子

根据式(7)和式(9)计算相关度高的IMF分量的Teager能量谱如图6所示。

将所得Teager能量谱进行快速傅里叶变换运算，得到的能量频谱与主要IMF频谱的对比，以及对原始故障信号进行HHT运算后所得到的希尔伯特边际谱的对比图如图7所示。

图6 Teager能量谱Fig.6 Teager energy spectrum

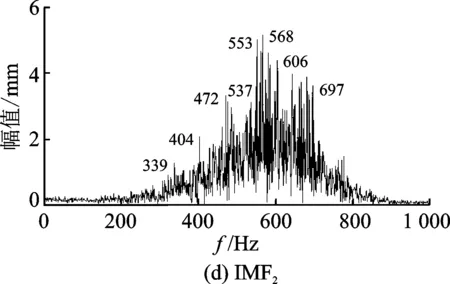
图7 对比图Fig.7 Comparison chart

结合图6和图7,从图7(a)与图7(b)的对比可以看出，信号不经消噪直接使用HHT处理后对于当前工况下的微弱故障特征提取效果不好,未能发现含有转频以及啮合频率的成分; 从图7(a)与图7(c)～(f)可以看出,主要的IMF分量中含有故障特征成分,但由于强噪声环境导致特征不明显。图7(a)在对有效IMF分量求取Teager能量谱及其频谱后，得到一些幅值较大的峰,其中24Hz的峰在转频附近,其能量较转频的能量低,但也有其倍频出现,由此可以初步推断齿轮箱的输入级出现故障,但是信号特征不明显,频谱中81，120和553 Hz等的能量较高,初步推测为齿轮箱的轴承所产生的,另外还有一些频率可能由于装配精度不足以及实验系统的其他部件所产生的,谱中696Hz的频率恰好在齿轮输入级的啮合频率附近,与图7(b)相比可以突出信号的微弱故障特征成分。对比相同载荷不同转速条件下该方法与传统方法的识别情况,如表4所示,可以看出本方法的有效性。

表4 识别效果Tab.4 Identification effect

由于小波基和分解层次的选取，导致改进方法未能在低转速情况下突出故障信息。

4 结 论

1) 采用改进小波阈值去噪方法对原始信号进行去噪处理,能有效提高信号信噪比、降低均方根误差。

2) 使用EEMD方法能够对故障信号进行自适应分解,并通过计算IMF分量与原信号的相关系数结合IMF的频谱,能够有效筛出虚假分量。

3) 采用Teager能量算子方法能够提取能量集中的IMF分量的能量谱,通过计算其频谱以及原信号的希尔伯特边际谱后,发现改进方法可以有效提取齿轮箱的故障特征频率。

[1] 姚廷强,迟毅林,黄亚宇,等. 刚柔耦合齿轮三维接触动力学建模与振动分析[J]. 振动与冲击,2009,28(2): 167-171.

Yao Tingqiang,Chi Yilin,Huang Yayu,et al. Contact dynamics modeling and simulation on rigid-flexible gear pair [J]. Journal of Vibration and Shock,2009,28(2): 167-171. (in Chinese)

[2] 王国彪,何正嘉,陈雪峰,等. 机械故障诊断基础研究“何去何从”[J]. 机械工程学报,2013,49(1): 63-72.

Wang Guobiao,He Zhengjia,Chen Xuefeng,et al. Basic research on machinery fault diagnosis-what is the prescription [J]. Journal of Mechanical Engineering,2013,49(1): 63-72. (in Chinese)

[3] 庞辉,方宗德,欧卫林. 多平行齿轮耦合转子系统的振动特性分析[J]. 振动与冲击,2007,26(9): 40-50.

Pang Hui,Fang Zongde,Ou Weilin. Analysis on lateraltorsional coupling vibration characteristics of multi-parallel gear-rotor system [J]. Journal of Vibration and Shock,2007,26(9): 40-50. (in Chinese)

[4] 冷军发,荆双喜,禹建功,等. EMD与能量算子解调在提升机齿轮箱故障诊断中的应用[J]. 煤炭学报,2013,38(2): 530-535.

Leng Junfa,Jing Shuangxi,Yu Jiangong,et al. Application of fault diagnosis method based on EMD and energy operator demodulation to hoist gearbox [J]. Journal of China Coal Society,2013,38(2): 530-535. (in Chinese)

[5] 李娟,周东华,司小胜,等. 微小故障诊断方法综述[J]. 控制理论与应用,2012,29(12): 1517-1529.

Li Juan,Zhou Donghua,Si Xiaosheng,et al. Review of incipient fault diagnosis method [J]. Control Theory & Applications,2012,29(12): 1517-1529. (in Chinese)

[6] 程军圣,于德介,杨宇. 基于EMD的能量算子解调方法及其在机械故障诊断中的应用[J]. 机械工程学报,2004,40(8): 115-118.

Chen Junsheng,Yu Dejie,Yang Yu. Energy operator demodulating approach based on EMD and its application in mechanical fault diagnosis [J]. Journal of Mechanical Engineering,2004,40(8): 115-118. (in Chinese)

[7] 李辉,郑海起,杨绍普. 基于EMD和Teager能量算子的轴承故障诊断研究[J]. 振动与冲击,2008,27(10): 15-17,22.

Li Hui,Zheng Haiqi,Yang Shaopu. Bearing fault diagnosis based on EMD and Teager kaiser energy operator [J]. Journal of Vibration and Shock,2008,27(10): 15-17,22. (in Chinese)

[8] 张德祥,汪萍,吴小培,等. 基于经验模式分解和Teager能量谱的齿轮箱故障诊断[J]. 振动与冲击,2010,29(7): 109-111,138.

Zhang Dexiang,Wang Ping,Wu Xiaopei,et al. Gearbox fault diagnosis based on empirical mode decomposition and Teager energy spectrum [J]. Journal of Vibration and Shock,2010,29(7): 109-111,138. (in Chinese)

[9] 林近山. 基于互补的总体经验模式分解算法的齿轮箱故障诊断[J]. 机械传动,2012,36(8): 108-111.

Lin Jinshan. Fault diagnosis of gearboxes based on complementary ensemble empirical mode decomposition [J]. Journal of Mechanical Transmission,2012,36(8): 108-111. (in Chineses)

[10] 张超,陈建军,郭迅. 基于EEMD能量熵和支持向量机的齿轮箱故障诊断方法[J]. 中南大学学报:自然科学版,2012,43(3): 932-939.

Zhang Chao, Chen Jianjun,Guo Xun. Gear fault diagnosis method based on ensemble empirical mode decomposition energy entropy and support vector machine [J]. Journal of Central South University:Science and Technology,2012,43(3): 932-939.(in Chineses)

[11] Wu Zhaohua,Huang N E. A study of the characteristics of white noise using the empirical mode decomposition method [J]. Proceedings of the Royal Society A Mathematical Physical & Engineering Science,2004,460(7): 1579-1611.

[12] 李辉,郑海起,唐力伟. 基于EEMD和THT的齿轮故障诊断方法[J]. 振动、测试与诊断,2011,31(4): 496-500.

Li Hui,Zheng Haiqi,Tang Liwei. Fault diagnosis of gearbox based on EEMD and THT [J]. Journal of Vibration,Measurement & Diagnosis,2011,31(4): 496-500. (in Chinese)

[13] 沈路,杨富春,周晓军,等. 基于改进EMD与形态滤波的齿轮故障特征提取[J]. 振动与冲击,2010,29(3): 154-157.

Shen Lu,Yang Fuchun,Zhou Xiaojun,et al.Gear fault feature extraction based on improved EMD and morphological filter [J]. Journal of Vibration and Shock,2010,29(3): 154-157. (in Chinese)

[14] Zhang Lijun,Xu Jinwu,Yang Jianhong,et al. Multiscalemorphology analysis and its application to fault diagnosis [J]. Journal of Mechanical Systems,2008,22: 597-610.

[15] 邵忍平,曹精明,李永龙. 基于EMD小波阈值去噪和时频分析的齿轮故障模式识别与诊断[J]. 振动与冲击,2012,31(8): 96-101.

Shao Renping,Cao Jingming,Li Yonglong. Gear fault pattern identification and diagnosis using time-frequency analysis and wavelet threshold de-noising based on EMD [J]. Journal of Vibration and Shock,2012,31(8): 96-101. (in Chinese)

[16] 胡爱军,孙敬敬,向玲. 经验模态分解中的模态混叠问题[J]. 振动、测试与诊断,2011,31(4): 429-434.

Hu Aijun,Sun Jingjing,Xiang Ling. Mode mixing in empirical mode decomposition [J]. Journal of Vibration,Measurement & Diagnosis,2011,31(4): 429-434. (in Chinese)

[17] 曹莹,段玉波,刘继承. Hilbert-Huang变换中的模态混叠问题[J]. 振动、测试与诊断,2016,36(3): 518-523.

Cao Ying,Duan Yubo,Liu Jicheng. Research and application of mode-mixing in Hilbert-Huang transform[J]. Journal of Vibration,Measurement & Diagnosis,2016,36(3): 518-523. (in Chinese)

[18] Lei Yaguo,He Zhengjia,Zi Yanyang. Application of the EEMD method to rotor fault diagnosis of rotating machinery [J]. Mechanical Systems and Signal Processing,2009,23(2): 1327-1338.

[19] Wu Zhaohua,Huang N E. Ensemble empirical mode decomposition: a noise assisted data analysis method [J]. Advances in Adaptive Data Analysis,2009,1(1): 1-41.