列车传动最优黏着控制策略研究

吴能峰， 钟立群， 杨北辉， 王辉华

(深圳市英威腾交通技术有限公司， 广东深圳 518100)

现代列车的牵引控制中，黏着控制是列车牵引传动控制的一个重要环节，列车牵引力的产生直接来源于轮轨间的黏着力[1-2]。通常，黏着系数随轮轨条件的变化而变化。当路面状况变得恶劣时，若司机手柄给的牵引力大于可利用的黏着力，列车会出现打滑或空转现象；当司机手柄给的牵引力小于当前路况可利用的最大黏着力时，列车的牵引和制动性能也会受到影响。因此，如何实现列车的最优化黏着已成为研究热点[3-6]。

文献[7]采用干扰观测器估计电机负载力矩，进而估算出轮轨间的黏着系数，该方法虽简单易行，但信号测量过程中含有较大噪声，会影响系统性能。由文献[8]可知，在黏着-蠕滑特性曲线的峰值处黏着利用可最大化，而黏着系数与蠕滑速度的微分定会引入高频干扰，因此，尽管文献[8-9]采用全维状态观测器估算黏着系数可降低测量噪声带来的影响，但在求取该曲线斜率k的过程中又会引入干扰。文献[10]为了减少微分带来的影响，采用最小二乘法计算斜率k；但最小二乘法其实是由卡尔曼滤波器演变而来，卡尔曼滤波器假定噪声满足高斯分布，而微分和路况变化时引入的噪声中必定含有不符合高斯分布的成分。要实现最优黏着，需让系统蠕滑速度达到最优蠕滑速度值，此时黏着-蠕滑特性曲线的斜率为零。文献[10]采用了力矩反馈型优化黏着控制，该方法虽简单但在黏着-蠕滑特性曲线的峰值点附近，不同曲线的斜率和黏着系数的关系差别较大，系统控制器的鲁棒性不强。文献[11]采用的模糊控制策略相比文献[7]采用的PI调节器可使得输出转矩平滑化，但控制复杂，编程困难。

为实现最优黏着，克服上述文献缺点，文中提出的列车最优黏着控制策略采用全维状态观测器估算黏着系数，为了更好地计算黏着-蠕滑特性曲线斜率对RLS的输入信号进行低通滤波，采用最速梯度法求得最佳蠕滑速度给定值，通过PI调节器得到转矩补偿值。通过仿真对其可行性进行了相关验证，结果表明该策略可实现最优黏着且控制简单易行。

1 列车单轴牵引动力学模型

1.1 黏着机理

列车牵引力的产生直接来源于轮轨间的黏着力，其中列车单轴牵引力模型如图1所示。图中Ft为列车牵引力，Fa为黏着力，Fr为列车行车阻力，M为单动轴分配质量，vt为车体线速度，ωw为车轮角速度，r为车轮半径。

图1 单轴列车牵引力模型

牵引模式时，随着车轮的滚动，车轮上被压缩的材质放松伸展开，钢轨则从被拉伸转变到被压缩，从而导致轮对的圆周线速度vw高于车体速度vt，两种速度之差为蠕滑速度vs，如式(1)所示。

vs=vw-vt

(1)

轮轨间的黏着力Fa为：

Fa=μa(vs)Wg

(2)

式中μa(vs)为黏着力系数，W为等效轴重，g为重力加速度。

黏着利用率β为：

(3)

式中μa,max为当前路况黏着系数最大值，μa为实际黏着系数。

典型黏着-蠕滑特性曲线如图2所示。

图2 典型黏着-蠕滑特性曲线

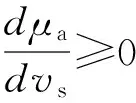
1.2 列车单轴牵引动力学模型分析

列车单轴牵引及机械传动部分包括牵引电机、齿轮箱、轮对和传动轴等部件，其简化等效图如图3所示。图中牵引电机将电能转化为机械能，在电机输出轴上产生力矩，通过齿轮箱与传动轴相连，再从传动轴传递到轮对。通过轮轨的蠕滑运动，力矩最终转化为黏着力使轮对沿钢轨滚动前进。

由牵引电机输出轴、轮对驱动轴及齿轮传动特性的动力学分析，可得：

轮对驱动轴转动方程：

(4)

牵引电机输出轴转动方程：

(5)

齿轮传动特性为：

(6)

Tmw=ηe·Rg·Twm

(7)

式中Bw轮轴摩擦黏滞系数，Bm电机轴摩擦黏滞系数，B为从电机侧看的等效黏滞系数，Rg为齿轮传动比，ηe齿轮箱传递效率。

图3 简化的列车单轴牵引力传递模型

根据式(7)、式(6)将式(4)折算到式(5)后可得牵引电机等效传动方程：

(8)

(9)

(10)

(11)

式中Jm为牵引电机转动惯量，Jw车轮转动惯量，Jeq为从电机侧看的等效转动惯量，TL为电机等效负载转矩。

根据列车动力学分析，可求得列车动力学方程：

(12)

(13)

式中a、b、c分别为空气动力系数。

根据上述动力学分析，忽略摩擦黏滞系数可构建列车单轴牵引动力学模型结构图如图4所示。

2 列车传动最优黏着控制策略

2.1 黏着系数的估算

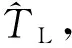
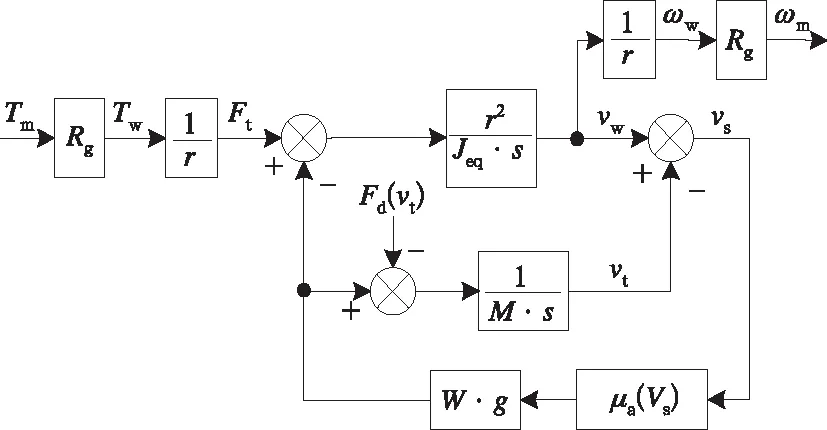
图4 列车单轴牵引动力学模型结构图

根据式(9)，可得状态空间表达式：

(14)

(15)

(16)

(17)

结合式(14)和式(17)，重构的电机负载转矩为：

(18)

黏着系数全维状态观测器结构图如图5所示。

2.2 基于RLS可变遗忘因子的黏着-蠕滑曲线斜率计算

图5 黏着系数全维状态观测器

(19)

式中，u代表输入信号，y代表输出信号。

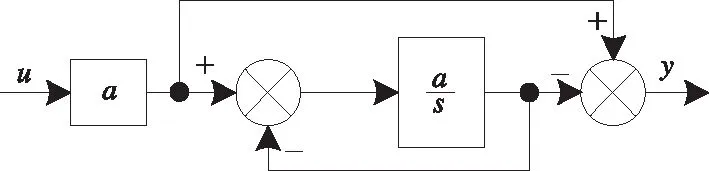
图6 微分低通滤波器的结构图

将图6中的积分环节离散化，则微分低通滤波器离散化的结构图如图7所示。

图7 微分低通滤波器离散化的结构图

基于RLS可变遗忘因子的自适应识别算法可表述为：

y(t)=φ(t)Tθ(t)

(20)

(21)

Q(t)=P(t)φ(t)

(22)

(23)

(24)

式中Q为系统过程噪声，P(t)为误差协方差，λ为加权因子，γ为遗忘因子。针对轨面黏着-蠕滑曲线斜率估算，则：

则式(20)～式(24)为：

(25)

(26)

(27)

(28)

(29)

当λ越接近1时，最小二乘法会记住前面所有数据；当 无限趋近于0时，将不会记住任何旧的数据。在实际应用中随着路况的改变，算法中之前的数据将不再记忆；若轨面环境不变，则算法将利用先前的数据迭代计算出更准确的估计值k。

2.3 最速梯度法

由图2可知，当处于稳定区时，一开始以较大的斜率几乎呈线性上升，越靠近峰值点斜率越小；当处于非稳定区时则相反，越远离峰值点斜率越小。因此，为了快速跟踪蠕滑曲线的峰值点，可采用最速梯度法求取蠕滑速度给定值为：

(30)

式中ζ与ξ为控制步长。当处于稳定区远离峰值电势，为了加快系统响应速度，可采用一个较大的固定步长；当靠近峰值点时，斜率通常无限趋近于0，为了避免系统进入非稳定区，可利用固定步长乘以斜率的方式来减慢逼近速度；当处于非稳定区时，为了加快恢复速度，可采用一个较大的固定步长。

蠕滑速度给定值vsref与其实际值vs的差经过PI调节器可得牵引电机力矩指令值的补偿量ΔT，即：

(31)

2.4 列车传动最优黏着控制策略原理分析

根据以上各节的描述可得列车传动最优黏着控制算法框图如图8所示。图中输入为：司机控制手柄T*，车体速度vt，电机转子角速度ωm和电机实际电磁转矩Tm；输出为：电机矢量控制转矩给定Tm*。

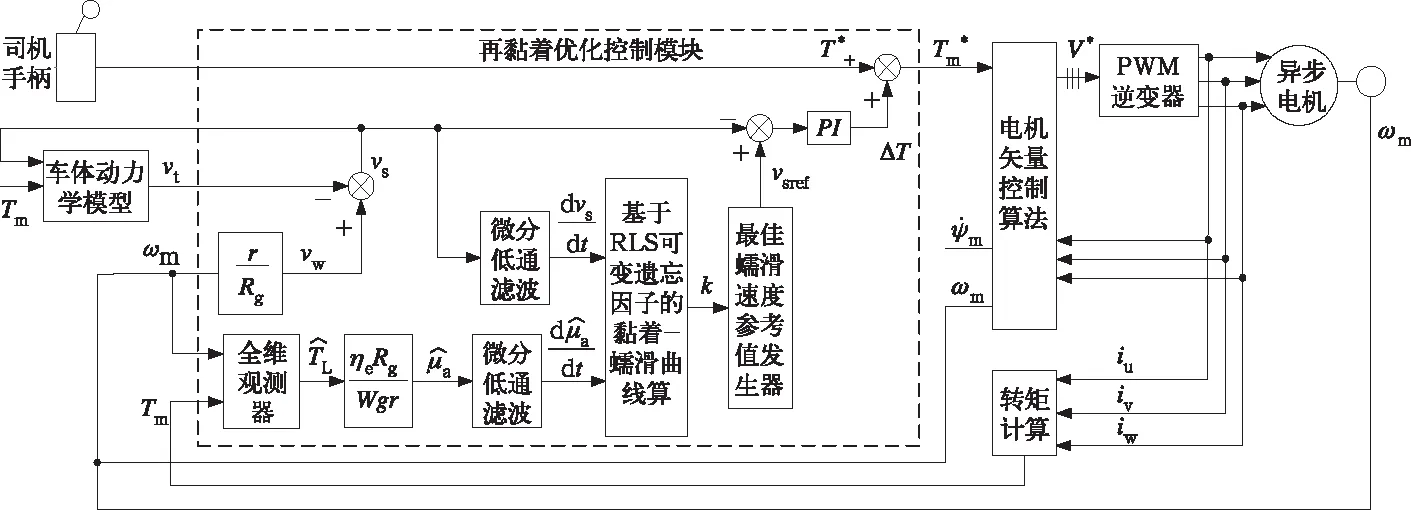
图8 列车传动最优黏着控制算法框图

3 仿真分析和试验验证

为验证列车传动最优黏着控制策略的正确性，利用MATLAB软件建立了列车单轴异步电机矢量控制系统仿真模型。在时刻分别为0，5，10，15 s时，进行了如图2中的路况切换，即干燥—湿轨道1-湿轨道2-干燥的仿真研究，所得仿真结果波形如图9～图14所示。系统仿真参数如表1所示。

图2中的干燥轨面、湿轨面1、湿轨面2的最大黏着系数μa,max分别为0.186，0.1，0.055，对应的最优蠕滑速度分别为1.2，2.2，1.6 m/s。由图9可知，利用全维状态观测器观测出的黏着系数可无静差地跟踪其实际值。由图10可知，蠕滑速度实际值vs可实时地跟踪其指令值vsref，稳态时可达到当前路况的最优蠕滑速度值，说明蠕滑速度PI控制器具有良好的静动态性能。由图11可知，电机转矩Tm可快速地响应其指令值Tm*，尽管司机手柄给定转矩在整个仿真过程中均为1 500 N·m，但电机转矩指令值在电机补偿转矩的动态调节下可实时得到更新，实现了列车最优黏着控制。 根据图12可知，当路况发生突变时，车轮速度得到了很好的控制并没有出现打滑现象。由图13得，当系统稳定时，斜率k无限趋近0，验证了上述结论的正确性。

综上所述，列车不管处在何种路况，其通过文中提出的最优黏着控制策略均能迅速地实现当前路况的最优黏着，调整时间短，稳态时几乎无波动且黏着利用率可无限接近100%。

表1 系统仿真参数

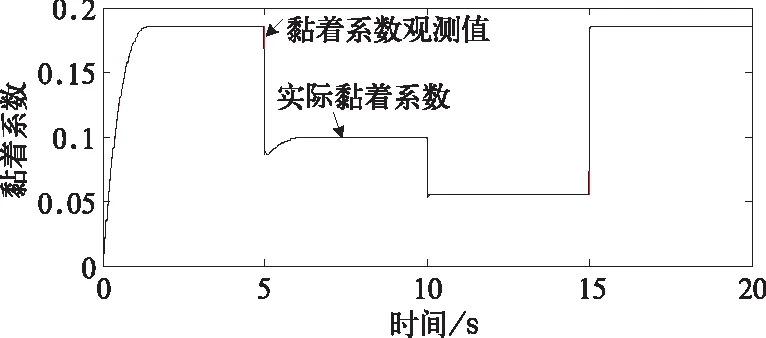
图9 黏着系数实际值与观测值

图10 蠕滑速度指令值与实际值

图11 牵引电机转矩指令值与实际值

图12 列车速度与车轮速度

图13 黏着-蠕滑特性曲线斜率

图14 黏着利用率

4 结 论

在分析了列车黏着机理和单轴牵引动力学模型的基础上，提出了列车传动最优黏着控制策略，采用全维状态观测器估计出黏着系数，对黏着系数和蠕滑速度对时间的微分进行了低通滤波，采用基于RLS可变遗忘因子的滤波器得到黏着-蠕滑特性曲线斜率k，根据最速梯度法可求出最优蠕滑速度给定值，利用蠕滑PI控制器可求出牵引电机动态转矩补偿值实现了最优黏着目标。仿真结果验证了该算法的可行性和有效性，且系统具有良好的动静态性能。

[1] Sajad Sadr, Davood Arab Khaburi, Jose Rodríguez, et al. Predictive Slip Control for Electrical Trains [J]. IEEE Transactions on Industrial Electronics,2016,63(6):3446-3457.

[2] Xiang Hong, Ruihua Zhang, Lin Wu,et al. Simulation of Adhesion Control Method Based on Phase-shift[C]∥Busan, Korea: 2013 International Conference on Electrical Machines and Systems,2013:2077-2080.

[3] 李江红，胡云卿，彭辉水，等.轨道交通黏着利用控制的关键技术与方法[J].机车电传动,2014(6):1-5.

[4] 王赛，杨中平，林飞，等. 基于dSPACE 的牵引传动系统黏着利用控制半实物仿真平台研究[J].机车电传动,2014(2):26-30.

[5] 魏家麒，张开林，姚 远. 单轴牵引力变化时的机车轴重转移分析[J]. 机车电传动,2014(3):40-43.

[6] 秦金飞. 高速列车滑行时制动力再分配策略研究[D]. 北京:北京交通大学,2013.6.

[7] K.Ohishi, K.Nakano, LMiyashita and S.Yasukawa, Anti-Slip Control of Electric Motor Coach Using Adhesion Force Coefficient Estimatior Based on Disturbance Observer[J]. Tkans of IEEJ,1999,119-D,(6):802-808.

[8] 林文立，刘志刚，孙大南, 等. 基于最优黏着利用的地铁牵引电机并联控制策略[J]. 电工技术学报,2010,25(6):24-30.

[9] 林文立，刘志刚，方攸同. 地铁列车牵引传动再黏着优化控制策略[J]. 西南交通大学学报,2012,47(3):465-470.

[10] 胡亮，杨中平，林飞. 高速列车牵引传动优化黏着控制方法研究[J]. 电气传动,2015,45(3):53-57.

[11] Kwon S K，Huh U Y，Kim H I，et al. Re-adhesion Control with Estimated Adhesion Force Coefficient for Wheeled Robot Using Fuzzy Logic[C]∥Busan，Korea: 30th Annual Conference of the IEEE Industrial Electronics Society，2004：2530-2535.

[12] 胡寿松. 自动控制原理[M]. 北京：科学出版社,2007.