基于Akima-LMD和GRNN的短期负荷预测
2018-03-05邹红波伏春林
邹红波, 伏春林, 喻 圣
(三峡大学电气与新能源学院, 湖北 宜昌 443002)
1 引言
短期负荷预测是电力系统能量管理系统的重要组成部分,是调度运行安排、生产计划的基础,提高对电力负荷预测的准确率对于电网的安全经济性有着十分重要的意义。电力负荷受经济、政治、气候、电价等多方面因素影响,尤其是气候影响最为突出[1],多因素的综合影响下,电力负荷序列成为一种非平稳、非线性的随机序列,又具有拟周期性的特点[2,3]。
目前,使用较为广泛的短期负荷预测方法包括持续法[4,5]、支持向量机[6-9]、卡尔曼滤波法[10-12]、神经网络法[13-15]、时间序列法[16,17]等,其中,神经网络法最为常见。传统神经网络法需要大量的样本来训练网络,可能使预测的结果出现局部最优。文献[18]提出广义回归神经网络(Generalized Regression Neural Network, GRNN),该预测方法能局部逼近网络,具有良好的非线性映射能力,相比传统神经网络法,网络模拟效果好,计算速度快,结果稳定,更适合预测具有非线性和非平稳性的序列。
电力负荷序列分解的常见方法有小波分析[19]、滤波法[20]、经验模态分解(Empirial Mode Decomposition, EMD)[21,22]、局域均值分解(Local Mean Decomposition, LMD)[23]等。其中小波分析分解效果取决于基函数和层次的选择,自适应性差;EMD自适应性强,但存在频率混叠、无法避免端点效应和过包络等问题;文献[23]指出,LMD较EMD法迭代次数明显减少,端点效应较轻,对于调频调幅的非平稳信号进行模态参数识别有很高的精度。但鉴于LMD法的过平滑性[24],文献[18]采用Akima插值法代替滑动平均法改进LMD来减小过平滑的影响。
本文采用基于改进LMD和GRNN的模型[24]预测短期电力负荷。其简要过程为:首先将改进后的LMD算法用于电力负荷序列的分解,得到高频到低频的电力负荷序列子分量;然后运用GRNN神经网络对各分解分量分别建模预测;最后将各预测结果叠加得出最终电力负荷预测值。仿真对比现有EMD和GRNN的模型,表明了该方法在预测短期负荷中的优越性。
2 插值的LMD算法
2.1 Akima插值原理
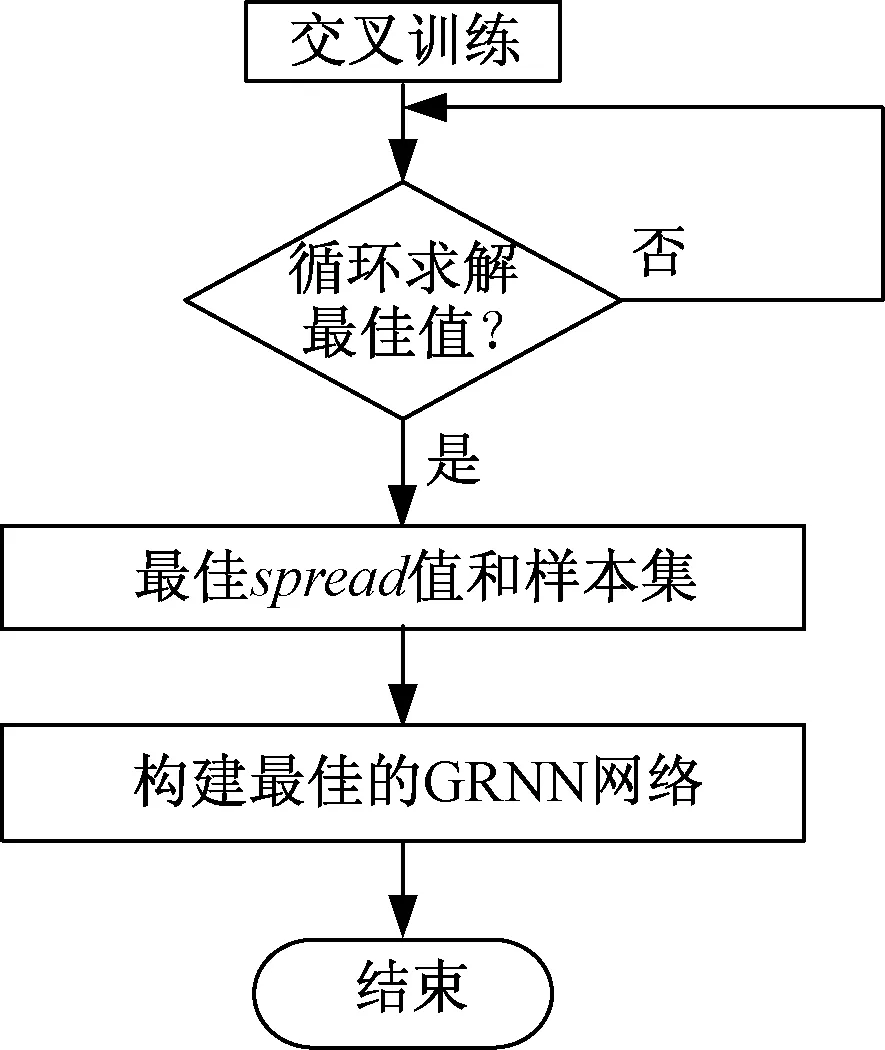
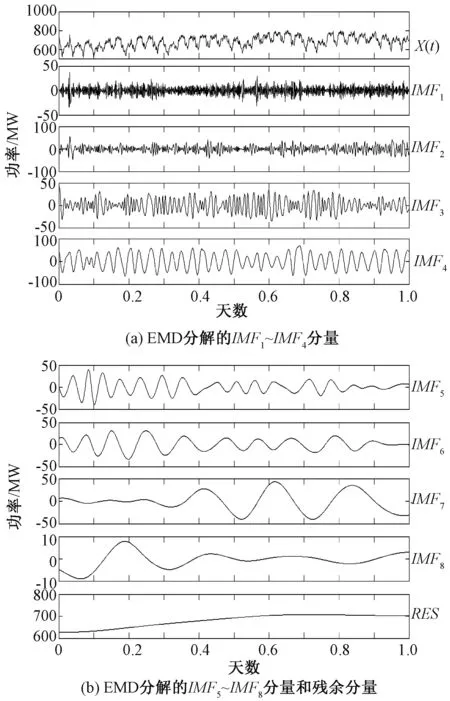
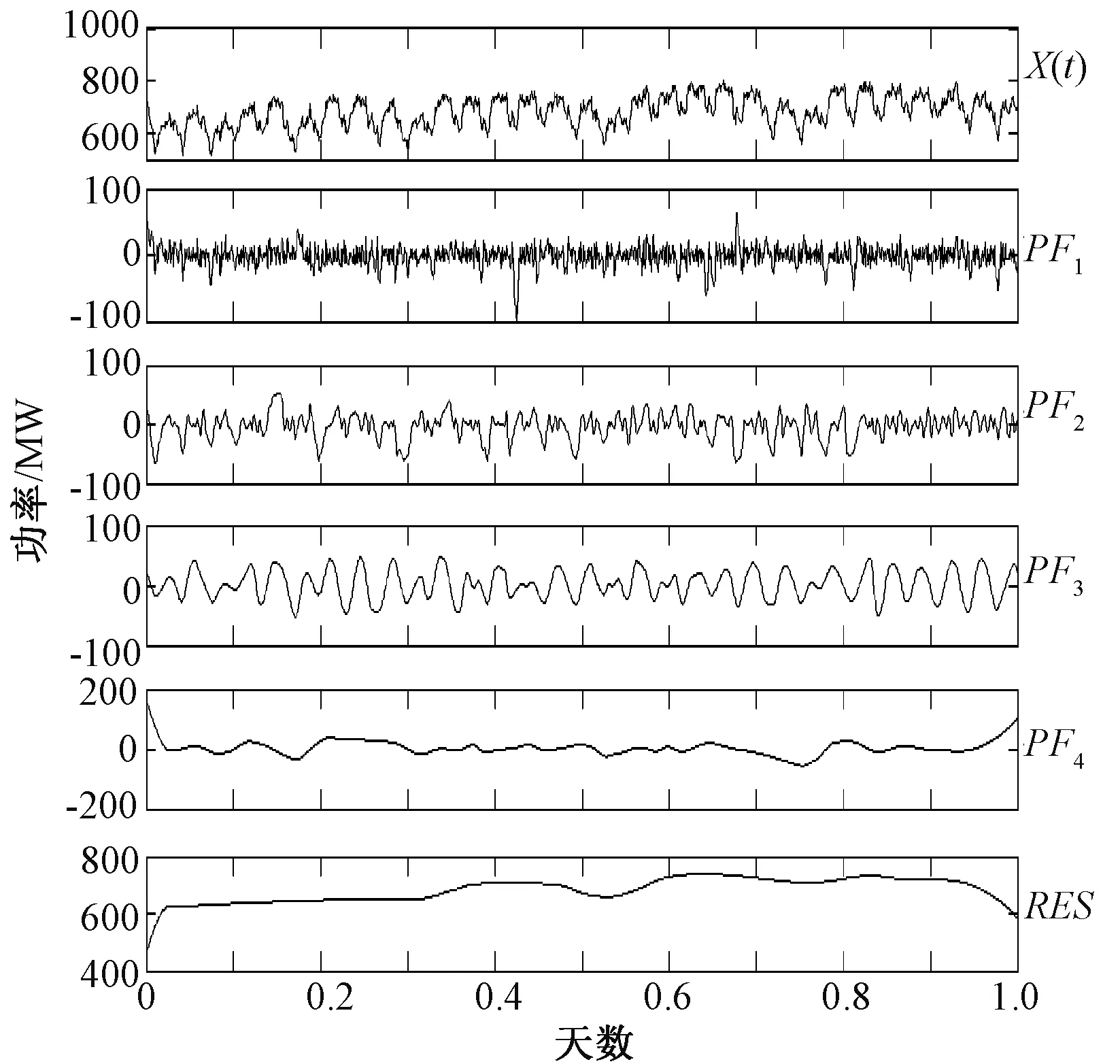
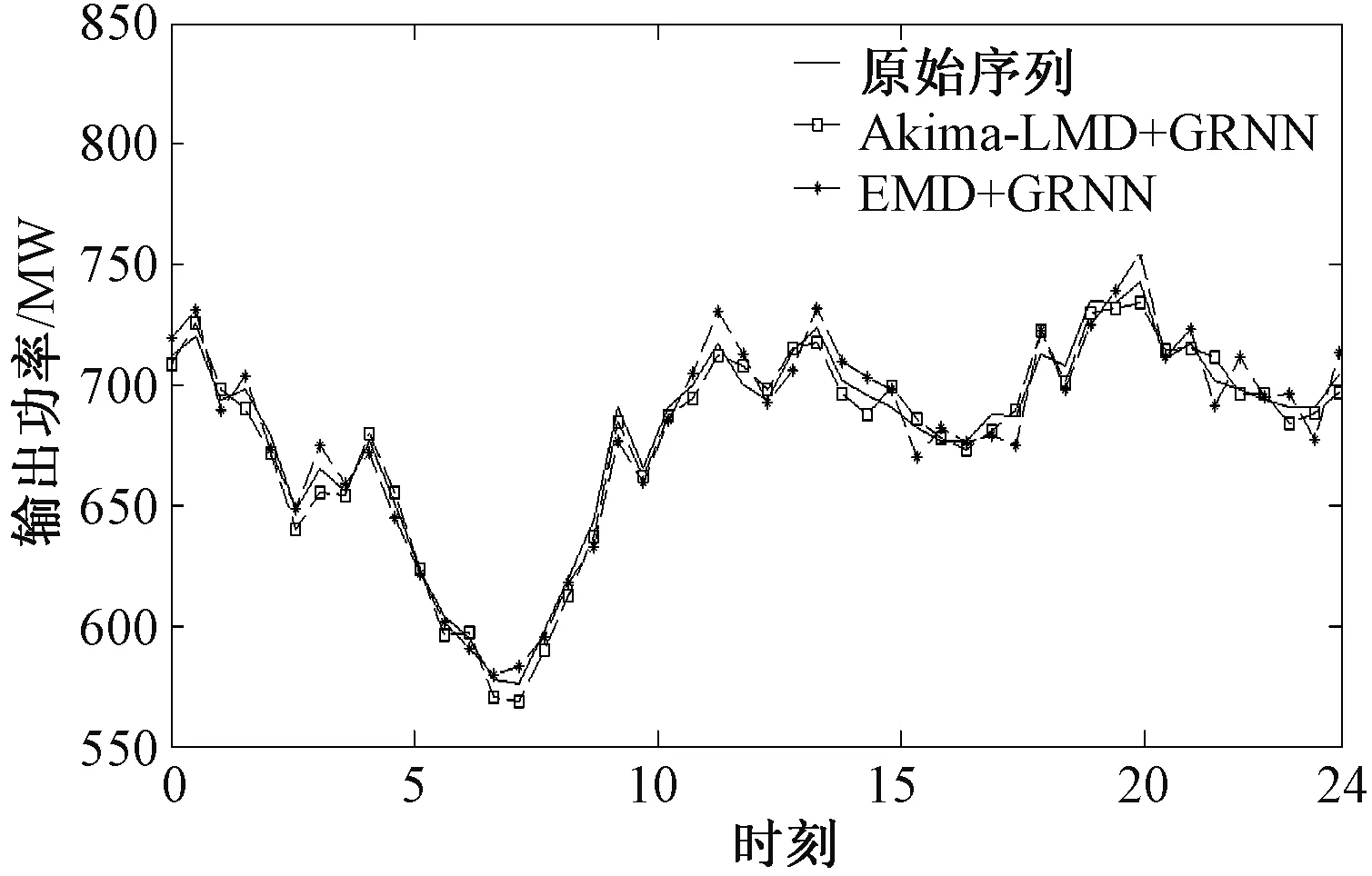
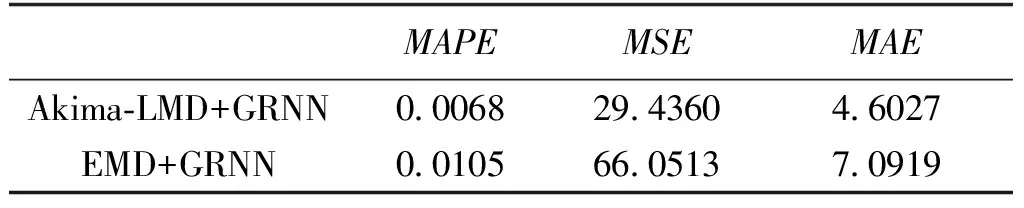
设平面上n个不等距结点(xi,yi)(i=0,1,…,n-1),其中x0 (1) 在此区间上可以确定唯一的三次多项式: (2) 式中,A~D为系数。 根据式(2)计算该子区间上各个插值点的函数值,其中多项式的各个系数按照如下步骤求解。 根据Akima提出的用5个数据点来估计出中间点导数的几何条件,可由式(3)、式(4)计算gk和gk+1: (3) (4) (5) 最后,可以求得在子区间[xk,xk+1]上的三次多项式的系数为: (6) 应用上述插值方法,就可对数据序列进行插值拟合,得到序列上下包络的曲线方程。 LMD算法将非平稳信号自适应地逐级分解为若干个PF(Product Function)分量,分解的PF分量从高频到低频排列。一个复杂的信号可以看作是一个多分量的信号的合成,通过LMD的分解可以解析出若干个PF分量,PF分量实质上由一个纯调频信号和一个包络信号的乘积得到,对PF分量进行瞬时频率和幅度的Hilbert分析更能看出信号所包含的物理意义。其分解过程如下: (1)求出纯调频函数 找出信号的所有局部极值点ni,包括极大极小值点,对全部相邻的极值点求平均值: (7) 采用滑动平均值插值法将全部相邻的平均值点mi连接起来,得到局部均值函数m11(t)。则定义包络估计值为: (8) 采用滑动平均值插值法将全部相邻的包络估计值ai连接起来,得到包络估计函数a11(t)。从原信号x(t)中分离出局部均值函数m11(t),得到h11(t): h11(t)=x(t)-m11(t) (9) h11(t)与a11(t)相除,实现对h11(t)解调,得到s11(t): (10) 如果s11(t)成为一个纯调频函数,则它的局部包络函数a12(t)=1。如果a12(t)≠1,则需要继续重复上一过程,直至a1n(t)=1位置,s1(n-1)(t)就是所需要的纯调频函数。 (2)求出包络信号的PF分量 包络信号a1(t)为迭代过程中产生的所有包络估计函数的乘积,其表达式为: (11) 包络信号a1(t)乘以纯调频信号s1(n-1)(t)得到原始信号分解后的第一个分量PF1(t): PF1(t)=a1(t)s1(n-1)(t) (12) 从原始信号x(t)中分离PF1(t)得到一个新的信号x1(t): x1(t)=x(t)-PF1(t) (13) 将x1(t)作为原始信号重复以上步骤,分解出PF2(t),…,PFk(t),直至xk(t)是一个单调函数为止。所以,原始信号可以分解为k个PF和xk(t),即 (14) 通过LMD的方法,一个多分量非平稳信号分解为若干个单分量信号的叠加,且分解过程从高频到低频,没有造成原始信号的失真。 GRNN神经网络的理论基础是非线性回归分析,非独立变量Y相对于独立向量的回归分析实际上是计算具有最大概率值的y。设f(x,y)为随机向量x和随机变量y的联合概率密度函数,X为x的观测值,则y相对于X的回归,即条件均值为: (15) (16) 当σ取值非常大时,估计值近似等于所有样本因变量的均值;当σ趋于0时,估计值和训练样本非常接近。 纵观《别裁》中有关李商隐的全部材料会发现,沈德潜在对李商隐诗歌创作成就上态度稍显矛盾,一方面认为义山诗讥刺过深,征引过多,失之自然,另一方面肯定其中却有大雅之作,风骨风格皆存,可立一宗。值得注意的是,在沈德潜认为讽喻过繁有失诗之雅的背景下,又大选有讥刺之意的义山诗,《马嵬》《隋宫》《南朝》《随师东》《曲江》《汉宫词》《宫妓》《齐宫词》《贾生》等都是义山诗中有名的讽喻诗,沈德潜对这些诗评价颇高,评《齐宫词》《贾生》“异体而各极其致”[5]683,评《隋宫》“用笔灵活”[5]507,且对这些诗中的讥刺之意都有仔细的解说,如在对《隋宫》的细解就很有见地: 当待预测点集中在训练样本中时,易导致预测值和样本中对应的因变量非常接近,如果被预测点不包含在训练样本中,则预测误差可能会比较大。只有当σ取合适值,并且将所有的训练样本考虑进去,才能有效提高预测精度。在Matlab中采用Crossvalind函数交叉验证训练神经网络,spread值从0.1~2s遍历,得到最佳的spread值,其程序主框图如图1所示。 图1 GRNN程序设计框图Fig.1 GRNN programming block diagram 将改进的LMD和GRNN相结合,建立一个新的预测模型。预测步骤如下: (1)使用改进的LMD方法分解电力负荷序列,得到相对平稳的从高频到低频的分量PFi和余量xi。 (2)探讨PFi分量与气温的相关度,相关度高则将气温作为神经网络的输入量,对不同频带的分量PFi和余量xi依据其大量的历史数据确定并建立样本数据,建立和训练相应的GRNN预测模型。 (3)将各预测值叠加得到最终电力负荷序列预测值。 为了评价建立的电力负荷预测模型,将预测序列和实际序列做数据对比,选取三个统计量:平均绝对百分比误差MAPE、平均绝对误差MAE、均方误差MSE。三个指标的表达式如下: (17) 图2 原始序列的EMD分解Fig.2 EMD decomposition of original sequence 图3 原始序列的Akima-LMD分解Fig.3 Akima-LMD decomposition of original sequence 在分量的质量上,IMF在幅度域分布较为平稳,呈现出拟周期性,PF分量中PF3分量明显反映了原序列的趋势(相关系数达到0.921),PF1和PF2反映数据序列的高频变化,具有强烈的非线性成分。 取EMD分解后每个IMF分量和残余分量的前30天的数据进行GRNN神经网络训练,一天的48个数据和第二天天气预报的平均气温为输入,第二天的48个数据为输出,得出分量第31天的预测集,再把预测集分别叠加得到原序列的第31天的预测序列。采用同样的方法处理LMD分解后的每个分量,得到原序列的第31天的预测序列。1月31号为周日,所以在训练网络需要增加周日的负荷数据作为输入以提高预测精度。为防止数据的量度不统一引起网络的饱和进而引起较大误差的情况,故在训练网络前对输入数据和输出数据进行归一化处理,输入数据归算到(-1,1)之间,输出数据归算到(0,1)之间,经过网络输出的预测值需要进行反归一化来还原。 比较EMD+GRNN与Akima-LMD+GRNN神经网络方法在第31天的电力预测结果,如图4所示。统计两个模型的参数,如表1所示。 图4 预测曲线与实际曲线对比图Fig.4 Contrast of forecast curve and actual curve MAPEMSEMAEAkima⁃LMD+GRNN0006829436046027EMD+GRNN0010566051370919 由表1可以看出,Akima-LMD+GRNN模型预测短期电力负荷相比EMD+GRNN方法具有更高的精度和预测稳定性,表明此方法适用于电力短期负荷预测。 本文分别采用EMD和Akima-LMD的分解方法对电力负荷序列进行分解对比,然后由GRNN神经网络预测各个分量,再叠加重构出负荷的预测趋势。由算例结果得出,Akima-LMD分解较EMD分解有更少的迭代次数,其PF3分量的瞬时幅度和瞬时频率反映了原始信号的真实信息。Akima-LMD+GRNN模型和EMD+GRNN模型相比具有更高的预测精度,因此该模型和EMD+GRNN模型相比更适用于短期电力负荷预测。 [1] 周潮,刑文洋,李宇龙(Zhou Chao, Xing Wenyang, Li Yulong).电力系统负荷预测方法综述(Review of the load forecasting methods of electric power system)[J].电源学报(Journal of Power Supply),2012, (6):32-39. [2] 隋惠惠(Sui Huihui). 基于BP神经网络的短期电力负荷预测的研究(Research on short-term electric load forecasting based on BP neural network) [D]. 哈尔滨:哈尔滨工业大学(Harbin: Harbin Institute of Technology), 2015. [3] 刘耀年,杨德友,庞松岭,等(Liu Yaonian, Yang Deyou, Pang Songling, et al.).基于经验模态分解与动态神经网络的短期负荷预测(Power system short-term load forecasting based on empirical mode decomposition and dynamic neural network)[J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy),2008,27(3):13-17, 53. [4] Sommer Matthias, Klink Michael, Tomforde Sven. Predictive load balancing in cloud computing environments based on ensemble forecasting[A]. IEEE International Conference on Autonomic Computing (ICAC) [C]. 2016. 300-308. [5] Taylor J W, Mcsharry P E, Buizza R, et al. Wind power density forecasting using ensemble predictions and time series models[J]. IEEE Transactions on Energy Conversion, 2009, 24(3): 775-782. [6] 王奔,冷北雪,张喜海,等(Wang Ben, Leng Beixue, Zhang Xihai, et al.). 支持向量机在短期负荷预测中的应用概况(Application profiles of support vector machine in short-term load forecasting)[J]. 电力系统及其自动化学报(Proceedings of the CSU-EPSA.),2011,23(4):115-121. [7] Mukherjee Sayan, Osuna Edgar, Girosi Federico. Nonlinear Prediction of chaotic time series using support vector machines[A]. 7th IEEE Workshop on Neural Networks for Signal Processing[C]. Amelia Island, USA, 1997. 511-520. [8] Suykens J A K, De Brabanter J, Lukas L, et al. Weighted least squares support vector machines: Robustness and sparce approximation [J]. Neurocomputing, 2002, 48: 85-105. [9] Lin Chun-Fu, Wang Sheng-De. Fuzzy support vector machines[J]. IEEE Transactions on Neural Networks, 2005, 13(2): 464-471. [10] 张民,鲍海,晏玲,等(Zhang Min, Bao Hai, Yan Ling, et al.).基于卡尔曼滤波的短期负荷预测方法的研究(Research on processing of short-term historical data of daily load based on Kalman filter)[J].电网技术(Power System Technology),2003,27(10):39-42. [11] Huelsemann S M. Short and ultra-short term load forecast by Kalman filter and autocorrelation[A]. Proceedings of the Universities Power Engineering Conference[C]. Edinburgh, UK, 1998. 497-500. [12] Aurobinda R, Ashok K P, Pao K P. A novel Kalman filter for frequency estimation of distorted signals in power systems[J]. IEEE Transactions on Instrumentation and Measurement, 2002, 51(3): 469-479. [13] Quaiyum S, Khan Y, Rahman S. Artificial neural network based short term load forecasting of power system[J]. International Journal of Computer Applications, 2011, 30(4): 1-7. [14] 潘雪涛(Pan Xuetao). 基于改进BP神经网络算法的短期负荷预测(Short-term load forecasting based on improved BP neural network algorithm)[J].上海电力学院学报(Journal of Shanghai University of Electric Power),2012,28(4):388-391. [15] 孔繁宁(Kong Fanning). 基于神经网络的大连地区短期电力负荷预测(Short-term electric load forecasting using neural network for Dalian district) [D]. 大连:大连理工大学(Dalian: Dalian University of Technology), 2013. [16] 杨正瓴,张广涛,林孔元(Yang Zhengling, Zhang Guangtao, Lin Kongyuan). 时间序列法短期负荷预测准确度上限估计(Upper limit estimating of short term load forecasting precision by time series analysis)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2004,16(2):36-39. [17] 孙英云,何光宇,翟海青,等(Sun Yingyun, He Guangyu, Zhai Haiqing, et al.).一种基于决策树技术的短期负荷预测算法(A short-term load forecasting method based on decision-tree approaches)[J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy),2004, 23(3):55-58, 75. [18] 雷庆坤,李生虎,陈曦鸣,等(Lei Qingkun, Li Shenghu, Chen Ximing, et al.). 基于改进的LMD和GRNN组合风速预测(Composite wind speed forecasting model based on improved LMD and GRNN)[J]. 合肥工业大学学报(自然科学版)(Journal of Hefei University of Technology (Natural Science)),2015,38(7):891-896. [19] 邰能灵,候志俭,李涛,等(Tai Nengling, Hou Zhijian, Li Tao, et al.). 基于小波分析的电力系统短期负荷预测方法(New principle based on wavelet transform for power system short-term load forecasting)[J].中国电机工程学报(Proceedings of the CSEE),2003,23(1):46-51. [20] 杨正瓴,张广涛,陈红新,等(Yang Zhengling, Zhang Guangtao, Chen Hongxin, et al.). 短期负荷预测“负荷趋势加混沌”法的参数优化(Parameter optimization in synthesizing load trend and chaotic components to short term load forecasting)[J].电网技术(Power System Technology),2005,29(4):27-30, 44. [21] 祝志慧,孙云莲,季宇(Zhu Zhihui, Sun Yunlian, Ji Yu).基于EMD和SVM的短期负荷预测(Short-term load forecasting based on EMD and SVM)[J]. 高电压技术(High Voltage Engineering),2007,33(5):118-122. [22] Balocchi R, Menicucci D, Varanini M. Empirical mode decomposition to an approach the problem of detecting sources from a reduced number of mixtures [A]. Proceeding of the 25th Annual International Conference of the IEEE EMBS[C]. Cancun, Mexico,2003. 3: 2443-2446. [23] 兰华,常家宁,周凌,等(Lan Hua, Chang Jianing, Zhou Ling, et al.).基于局部均值分解与神经网络的短期负荷预测(Power system short-term load forecasting based on local mean decomposition and artificial neural network)[J]. 电测与仪表(Electrical Measurement & Instrumentation),2012,49(5):48-51. [24] 张亢(Zhang Kang). 局部均值分解方法及其在旋转机械故障诊断中的应用研究(Research on local decomposition method and its application to rotating machinery fault diagnosis) [D].长沙:湖南大学(Changsha: Hunan University), 2012.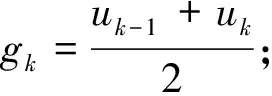
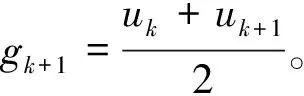
2.2 LMD算法
3 LMD和GRNN神经网络组合模型
3.1 GRNN神经网络的理论基础
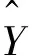
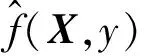
3.2 预测模型的建立
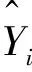
4 算例分析
5 结论
