多机组引水式水电站水轮机工作参数计算方法

杨素立，鞠小明

（1.四川大学水利水电学院，四川 成都 610065；2.四川大学水力学与山区河流开发保护国家重点实验室，四川 成都 610065）

1 引言

长隧洞多机组引水式水电站大多在引水隧洞末端布置调压室，其后的压力钢管分岔引水至各台机组。由于水轮机的工作水头与该机组的引水道水力损失密切相关，这样的布置方式使得电站各台机组即使在相同的出力条件下，水轮机的工作水头和引用流量也会略有差异，也就是各台机组的蜗壳压力不仅与该机组的运行出力有关，还与压力钢管分岔后的支管布置方式有关。水电站建设过程中，较长的发电引水隧洞往往会根据开挖揭示后的地质情况变更设计之初的衬砌方式，这样的变更直接影响机组的工作水头。水电站建成后，水轮机型号和模型综合特性曲线等资料已经完全确定，可以根据现场机组运行实测资料，反演计算发电引水隧洞的实际糙率或水力损失[1][2]，重新调整电站设计之初的水力计算模型，其中最主要的是重新调整发电引水隧洞的设计糙率值，从而使通过数学模型计算得到的实际机组运行中的水轮机工作参数，包括每台水轮机的出力、流量、水头、效率和导叶开度等数据更加精确可靠，便于掌握水电站的各种运行工况，为电站实际运行操作和数据分析提供必要的技术支撑。本文以某水电站为例，具体介绍这一计算方法。

2 长隧洞多机组水轮机工作参数计算方法

长隧洞水电站机组台数往往不止一台，受各台机组的引水流道影响，即使各机组的发电功率相同，理论上各台机组的水轮机工作水头和引用流量等参数均不会相同。以某引水式水电站为例，电站安装3台水轮发电机组，发电引水隧洞后接调压室，其后是压力钢管、2个岔管和支管后接3台机组，发电引水系统布置示意图如图1所示。图中Q1、Q2和Q3分别代表3台机组的引用流量。

图1 某水电站发电引水系统布置示意图

这是十分常见的布置方式，显然1号机组的流量Q1只经过了一个岔管，而2号、3号机组的流量Q2和Q3经过了2个岔管，加之各支管的长度不相同，因而相同功率下3台机组的水轮机工作水头是不相同的。根据上述引水系统布置计算简图，可以列出3台水轮机出力计算公式[3][4]：

式中：

上述公式中第一项为上游水库水位，第二项为厂房下游尾水位，第三项为引水隧洞和压力钢管主管中的水头损失，第四项和第五项为支管和尾水道中的水头损失。式中下标1、2、3代表机组编号，N为水轮机出力（kW），H为水轮机工作水头（m），Q为水轮机引用流量(m3/s)，n为水轮机效率；∇上为上游水库水位（m），∇下为下游尾水水位（m），λ、L、d、A 分别为各管段的沿程阻力系数、长度（m）、管径（m）和管道截面积（m2）；∑ζ1为引水隧洞和压力钢管主管中的所有局部损失系数之和，∑ζ2为1号机组3号支管和4号尾水道的所有局部损失系数之和，∑ζ3为2号机组5号支管和6号尾水道的所有局部损失系数之和，∑ζ4为3号机组8号支管和9号尾水道的所有局部损失系数之和。

将公式（4）、（5）和（6）分别代入公式（1）、（2）和（3）中，并先假定水轮机效率为已知（迭代计算后修正），可以得到：

压力引水道的沿程水头损失采用谢才—曼宁公式计算[5][6]，局部损失与损失系数有关。

式中：hf为沿程水力损失（m），R为水力半径（m），C为曼宁系数，L为管道长度（m），V为管道中流速（m/s），n为引水道的糙率，hj为局部水力损失（m），ξ为局部水力损失系数。

上述公式（7）、（8）和（9）是关于 Q1、Q2和 Q3的一组非线性方程组，联解上述方程组，可以得到相应机组的流量，进而再计算水头，算出单位转速和单位流量，在水轮机模型综合特性曲线上查得效率，与原先假定的效率进行比较，若不相等，继续以查得的水轮机效率代入后重新计算，直到查得的效率与前一次假定的效率基本相等为止，该迭代计算工作编写程序由计算机插值自动计算完成，其中水轮机模型综合特性曲线是以数据点的形式存储于计算机中[7][8][9]，需要将以单位转速和单位流量为纵横坐标的水轮机模型综合特性曲线进行离散，某水电站水轮机模型综合特性曲线如图2所示，离散后的水轮机效率和开度数据表如表1和表2所示。

图2 某水电站水轮机模型综合特性曲线图

表1 离散后的水轮机效率数据表

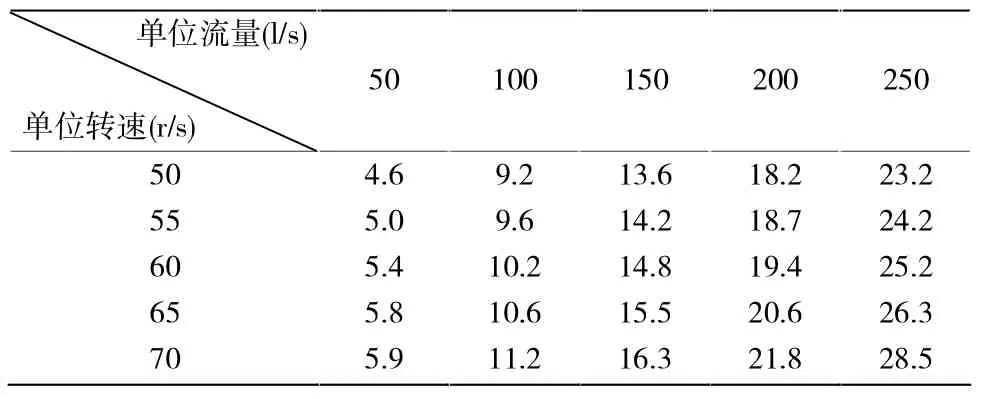
表2 离散后的水轮机导叶开度数据表

经过多次迭代计算，直到迭代计算得到的水轮机效率和前次迭代效率误差达到控制标准为止，例如可以控制效率迭代误差为0.05%或0.1%，这样的精度已经足够满足工程计算要求。

通过上述分析可见，电站机组实际运行时，水轮机的出力和工作水头、流量、导叶开度、水轮机效率等运行参数存在固定的对应关系。也就是说，在某一水库水位下只要给定水轮发电机组的出力，一定有某个水轮机的工作水头、流量、效率以及导叶开度与之对应。不同水电站的发电引水系统布置形式不同，构成各台水轮机工作水头中的水力损失也不相同，但是只要水电站的发电引水系统布置是确定的，水轮机的出力、工作水头、流量、效率以及导叶开度的对应关系就是确定的，这就是计算实际机组运行参数的理论依据。

3 计算实例

某水电站装机容量249(3×83)MW，设计引用流量74.1 m3/s。电站输水系统工程建筑物由进水口、引水隧洞、调压室及压力管道组成[10]。水库正常蓄水位2 857.00 m，死水位2 805.00 m，消落深度52.00 m。引水隧洞布置于左岸，隧洞总长14 436 m，采用马蹄形断面，其中Ⅲ类围岩占68.55%，长为9 893 m，过水断面面积为31.015 m2；Ⅳ类围岩占27.44%，长为3 959 m，过水断面面积为30.229 m2；Ⅴ类围岩占4.01%，长为579 m，过水断面面积为30.229 m2。调压室竖井内径6.0 m，竖井顶高程2 864.60 m，上室总长185 m。压力管道主管总长733.405 m，内径4.10 m，分岔引水至3台混流式水轮发电机组，支管直径1.9 m，1号支管长度94.88 m，2号支管长度84.36 m，3号支管长度107.41 m。

3.1 电站运行实测资料

该水电站运行中对大坝水位、调压井水位和机组出力等进行了记录，电站总负荷、机组运行台数和各台机组的负荷等实测运行资料如表3所示。实测资料中没有机组的开度和效率值，只有运行记录电站机组总引用流量值，其中序号1实测总流量3.83 m3/s，序号2实测总流量21.55 m3/s，序号3实测总流量42.5 m3/s，序号4实测总流量52.8 m3/s。

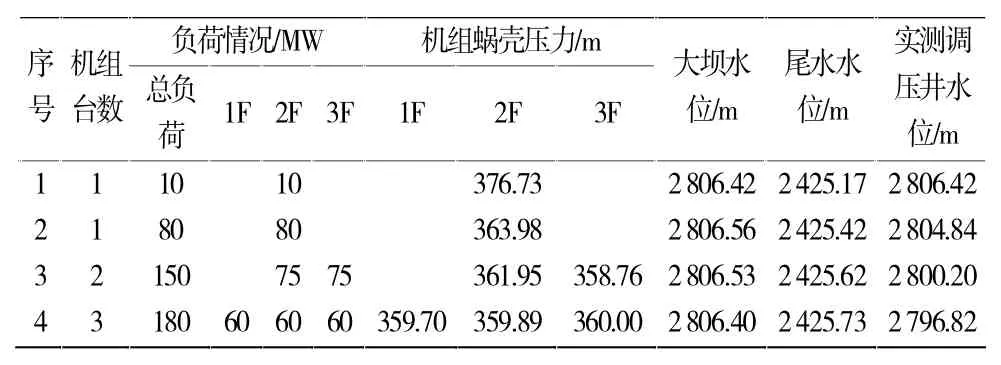
表3 不同负荷时机组运行实测资料

3.2 数学模型验证计算成果与实测资料对比分析

采用前述介绍的理论和计算方法，对某水电站实测资料相同工况进行数学模型验证计算，根据实测资料反推得到引水隧洞的衬砌糙率值为：Ⅳ类围岩和Ⅴ类围岩断面混凝土衬砌糙率值0.014，Ⅲ类围岩喷锚支护综合糙率由设计之初的0.0249调整为0.0219，岔管局部损失系数0.75，引水隧洞沿线局部水损系数根据施工后的实际转弯半径和断面变化计算取值，各工况的水轮机工作水头、流量、导叶开度和效率等如表4所示。计算的电站总流量略大于实测总流量，考虑到实际电站机组流量测量不够准确，这样的计算结果还是可以接受的。数学模型计算成果和实测记录数值对比如表5所示。

表4 对应实测工况的机组运行参数计算表

表5 数学模型验证计算与实测资料对比表

将实测资料与数学模型计算对比分析，机组蜗壳压力计算误差和调压井水位计算误差分别如表6、表7所示。

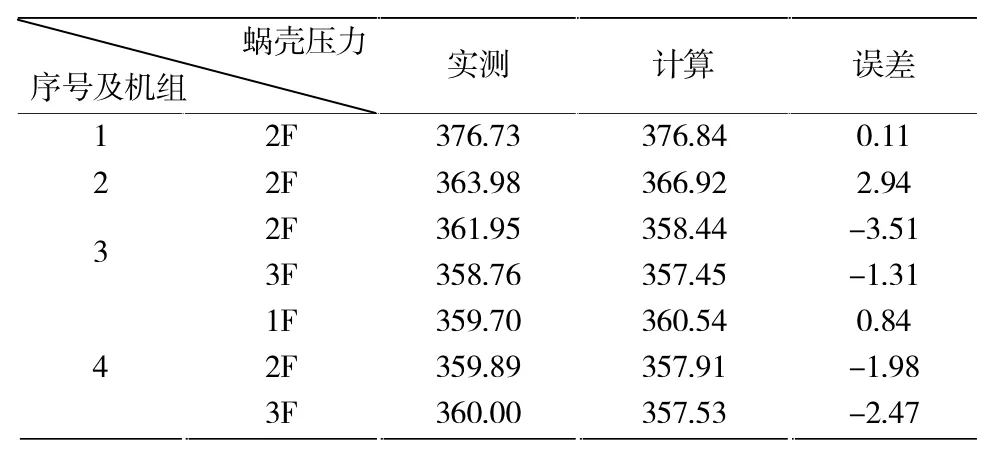
表6 蜗壳压力计算误差表 单位：m

表7 调压井水位计算误差表 单位：m

3.3 数学模型验证计算误差原因分析

分析水轮机蜗壳压力和调压井水位验证计算误差表6和表7可以看出，比较而言调压井水位计算的误差更小，计算值和实测值的误差在0.06～0.80 m，水轮机蜗壳压力计算值和实测值的误差在0.11～2.94 m，这样的计算精度已经足够满足工程需要。造成数学模型验证计算值和实测值有误差的原因主要有：首先是实际电站运行中尽管机组出力不变，但是根据观察调压井的水位并非完全是恒定的，有一个微小的波动范围，这与调压井的断面积大小有关，本例中的电站调压井竖井直径仅6.0 m，虽然满足小波动托马稳定断面积要求[11]，但是运行过程中仍有微小水位波动，造成实测值是一个变动范围；其次水轮机蜗壳压力计算值与机组引用流量和水轮机效率密切相关，计算中采用的水轮机效率是通过模型综合特性曲线离散后插值得到的效率，理论上原型水轮机效率会比模型水轮机效率略高[12]，通常原型和模型水轮机效率有1%～2%的误差，但是这一误差在不同的工况点是不相同的[3]，这也是造成水轮机蜗壳压力计算误差的原因之一。从算例可以看出，数学模型验证计算值和实测数据值基本吻合，说明这种计算方法对实际电站工程是有效可行的。

4 结语

根据电站运行实测资料，调整电站设计之初的水力计算模型，可以精确计算得到运行中的每台水轮机的出力、流量、水头、效率和导叶开度等数据,为电站实际运行和数据分析提供必要的技术支撑。从上述电站1台机组、2台机组和3台机组的运行参数数学模型验证计算表明，无论是调压室水位还是蜗壳的压力，本文提出的机组运行参数计算数学模型和计算方法基本能够反映电站机组的实际运行工况，并且计算结果与实测结果十分接近,这种数学模型和计算方法可以为水电站根据不同的水库水位制定相应的运行策略提供理论依据。

[1]齐英.不同糙率推求方法在引水隧洞中的对比分析[J].水利技术监督，2016（02）.

[2]陈文熙.基于一维非恒定流数学模型的辽宁省引水隧洞糙率推求研究[J].水利技术监督，2015（04）.

[3]郑源，陈德新.水轮机[M].北京：中国水利水电出版社，2011.

[4]戴荣法.水电站的流量率定[J].水文，1987（05）.

[5]吴持恭.水力学[M].北京：高等教育出版社，2003.

[6]吕文舫.曼宁公式应用在急变流的探讨[J].灌溉排水，1993（04）.

[7]邓杰，陈锐.水轮机综合特性曲线的数字化处理[C]//水轮发电机组稳定性技术研讨会论文集，2007.

[8]董宏成.水轮机综合特性曲线的计算机处理[J].水电站设计，1992（3）：59-62.

[9]刘文静，袁小宁，李大成，等.计算机数据采集系统在水电站压力引水系统水力学模型试验中的应用[J].西北水力发电，2002，18（4）.

[10]马善定.水电站建筑物[M].北京：中国水利水电出版社，1982.

[11]王树人.调压室水力计算理论与方法[M].北京:清华大学出版社,1983.

[12]李耀辉.原型水轮机效率计算公式的评析[J].云南水力发电，2001，17（1）.