履带变构式轮履复合爬楼轮椅爬楼平稳性分析
2018-03-05曹冲振王凤芹陈京邦
曹冲振,周 娜,王凤芹,陈京邦
(1.山东科技大学 交通学院,山东 青岛 266590;2.山东科技大学 机械电子工程学院,山东 青岛 266590)
1 引言
轮履复合式爬楼轮椅由于其兼具履带爬楼平稳和轮子平地行走灵活的优点而具有良好的发展前景[1-2]。在轮履复合爬楼轮椅的设计过程中找到合适的轮履复合方式是一个关键问题,同时为了保证乘坐者乘坐的舒适性和安全性,爬楼轮椅在履带爬楼过程中的平稳性更是设计过程中需要考虑的关键问题。研究一种基于行走轮摆动的履带变构式轮履复合爬楼轮椅[3],对其爬楼过程中的平稳性、安全性进行分析。并通过样机试验验证分析结果。
2 爬楼轮椅结构
基于大轮摆动的履带变构式轮履复合爬楼轮椅巧妙结合了普通轮椅和履带爬楼机,平地行走状态和爬楼状态的整体模型,如图1所示。主要包括轮椅架、摆臂大轮和履带爬楼机构。轮椅架即为普通轮椅的轮椅架;摆臂大轮为普通轮椅的行走大轮固定在摆臂机构上,由摆臂电机驱动,可以相对履带爬楼机构摆动;履带爬楼机构由折叠电机驱动,可以通过折叠变构置于轮椅座椅下方[3]。
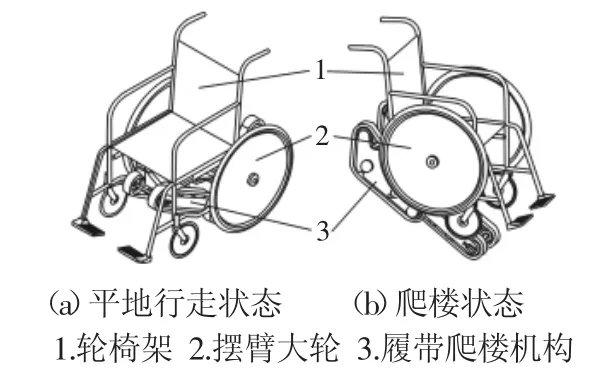
图1 整体模型Fig.1 The Model of this Project
3 爬楼轮椅爬楼平稳性分析
3.1 均匀楼梯上的爬楼平稳性分析
假设楼梯是均匀的。爬楼轮椅在爬楼过程中,爬楼履带底部的支撑有时是两条台阶沿,有时是三条台阶沿。在刚刚变成两条台阶沿支撑或者即将由两条台阶沿支撑变成三条在支撑时,爬楼轮椅的重心位于两条台阶沿支撑的极限位置,爬楼轮椅处于最不稳定的状态。两个临界状态的建模,如图2所示。B点为轮椅以及乘坐者的重心,A、C为履带底平面两端点(线),D、E、F为台阶沿。图中已知量L1=AB=780mm,L2=BC=475mm,L3=AC=750mm,∠β=36.08°,∠δ=75.42°;变量b、h、γ分别为楼梯的宽度、高度和楼梯倾角。

图2 均匀楼梯的爬楼平稳性分析数学建模Fig.2 The Mathematical Model of Stair Stability Analysis
由平稳性要求可知,为了保证履带爬楼的平稳性,必须使重心B位于两个支撑点(线)之间[4-5]。即图2(a)状态时重心需位于E点左侧,保证爬楼轮椅的后平稳性:L2cos(δ-γ)>b (1)
图2(b)状态时重心需位于E点右侧,保证爬楼轮椅的前平稳性:L1cos(β+γ)>b (2)

民用建筑设计准则中规定,住宅公共楼梯台阶尺寸最小台阶宽度为260mm,最大台阶高度为175mm[6]。常见住宅公共楼梯参数为高度(150~175)mm,宽度(260~300)mm。用MATLAB作函数f(b,h)和g(b,h)图像,为了方便划分网格,使运算的矩阵维数匹配,图中宽度b采用范围(250~300)mm。结果,如图3所示。
图3中间平面为z=0的平面,上侧曲面表示函数f(b,h),下侧曲面表示函数g(b,h)。在b,h的取值范围内,两个函数曲面和z=0平面都没有交点,两个不等式都成立,即现有结构参数的履带变构式爬楼轮椅在常见楼梯上都能够满足平稳性要求。
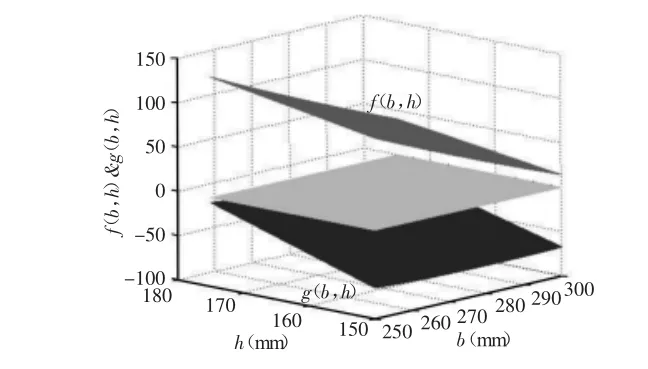
图3 f(b,h)和g(b,h)函数图Fig.3 Plots of f(b,h)and g(b,h)
为了增加爬楼轮椅安全系数方面的保障,需要进一步确定该爬楼轮椅在现有结构参数下的爬楼平稳性裕度[7]。所谓爬楼平稳性裕度定义为:履带爬楼处于图2所示两个最不稳定的临界状态时,爬楼轮椅和乘坐者整体重心位置分别到相近台阶沿的水平距离与台阶宽度的比值,平稳性裕度大于0,说明爬楼平稳。平稳性裕度表达式如下:后平稳性裕度
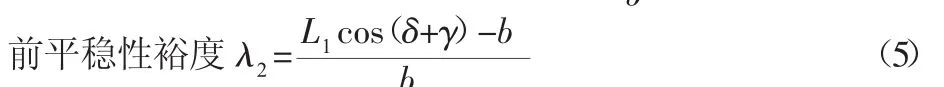
代入数值化简得到关于b、h的函数,并用MATLAB作函数图像,如图4所示。图中λ1曲面为后平稳性裕度函数图,λ2曲面为前平稳性裕度函数图。由图可知在常见尺寸的楼梯上后平稳性裕度λ1>0.044,前平稳性裕度λ2>0.025,说明爬楼轮椅爬楼平稳。
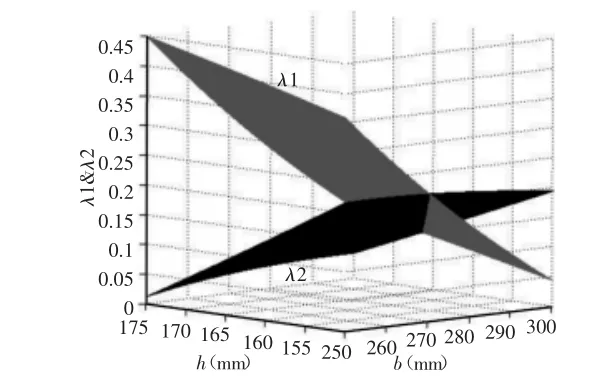
图 4 λ1和 λ2函数图Fig.4 Plots of λ1and λ2
3.2 非均匀楼梯上的爬楼平稳性分析
实际生活中的楼梯基本都是不均匀的,存在某一台阶突高、突低、突宽和突窄等情况。爬楼轮椅在非均匀楼梯上的爬楼过程肯定不是完全平稳的,但是在楼梯参数合适时,爬楼轮椅的爬楼过程能够波动最少,爬楼最平稳。因此非均匀楼梯时的爬楼平稳性要求为爬楼过程最平稳。下面分别根据几个不均匀因素单独存在时该爬楼轮椅的爬楼过程,通过数学建模,分析该爬楼轮椅的爬楼平稳性。当存在某一台阶突高时爬楼轮椅的上楼过程,如图5所示。部分参数参照图2。图中D、E、F、H为台阶沿,台阶沿F处的台阶突高,高为
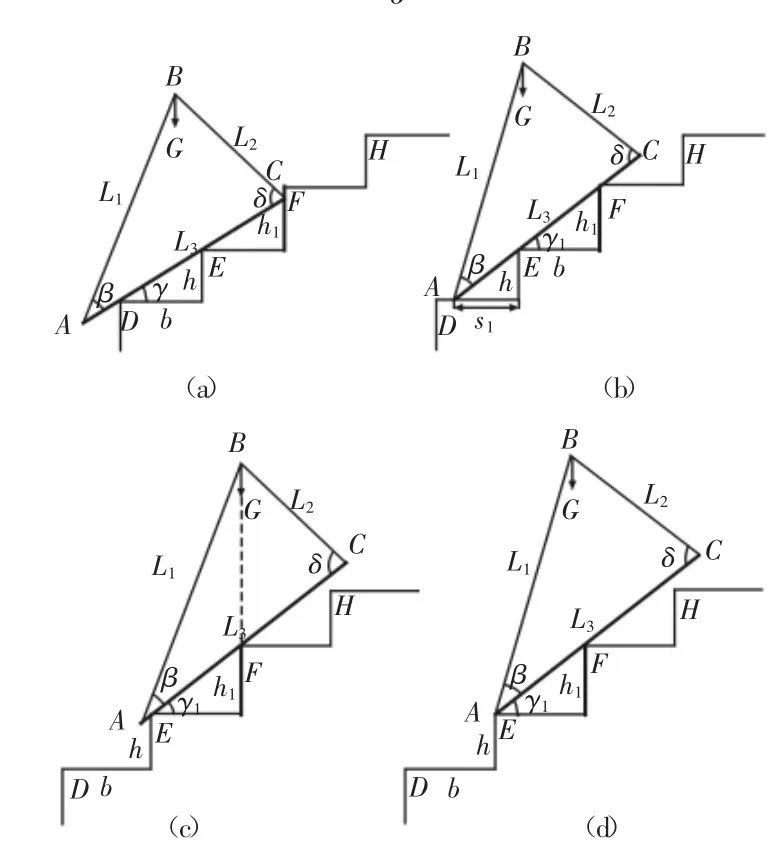
图5 越过突高台阶的上楼过程Fig.5 The Process of Climbing up a Higher Step
图5(a)中履带底平面后端点(线)C和F台阶沿所在台阶的立面处于接触临界状态,为了保证爬楼轮椅不会在C点接触该台阶立面之前就发生后仰,此时重心B在水平面上投影的位置必须位于台阶沿 E 的左侧,即有:L2cos(δ-γ)>b (6)
图5(b)中履带底平面前端点(线)A和D台阶沿所在台阶的水平面处于临界接触状态,为了保证爬楼轮椅不会在A点离开该台阶水平面之后发生前倾,此时重心B在水平面上投影的位置必须位于台阶沿 E 的右侧,即有:L1cos(β+γ1)>s1(7)
图5(c)中爬楼轮椅和乘坐者整体的重心恰好位于F台阶沿的正上方,爬楼轮椅即将绕F台阶沿后仰。若履带底平面后端点(线)C与台阶沿F的距离小于台阶沿F和台阶沿H的距离,即FC<FH,此时发生后仰,履带会先支撑在H台阶沿所在台阶的台阶立面上,继续上行后履带再由台阶沿H支撑,此过程中爬楼轮椅俯仰波动较大,平稳性较差;若履带底平面后端点(线)C与台阶沿F的距离大于台阶沿F和台阶沿H的距离,即FC>FH,此时发生后仰,履带底平面就能够直接支撑在台阶沿H上,爬楼轮椅爬楼平稳性最好。所以为了保证爬楼轮椅在爬楼过程中平稳性最好,要使 FC>FH,即有:
图5(d)中履带底平面前端点(线)A和E台阶沿处于临界接触状态,为了保证此状态之后爬楼轮椅能够由台阶沿A和台阶沿F支撑变成台阶沿F和台阶沿H支撑,此状态时重心B在水平面上投影的位置必须位于台阶沿F的右侧,即有:

式(6)至式(9)联立化简之后得:

当存在某一台阶突高时爬楼轮椅的下楼过程,如图6所示。部分参数参照图2和图5。
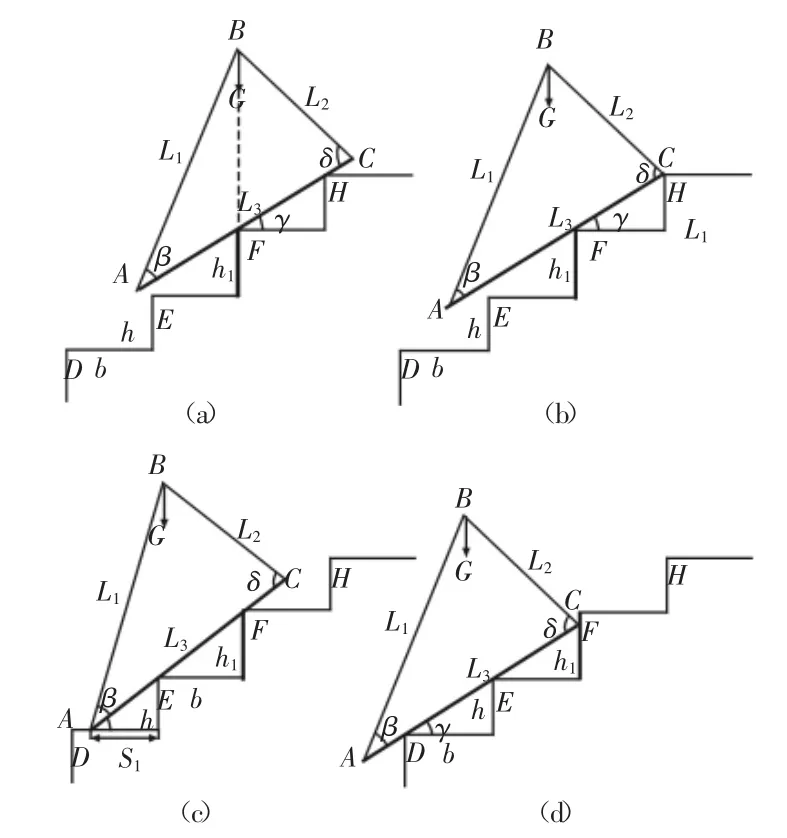
图6 越过突高台阶的下楼过程Fig.6 The Process of Climbing down a Higher Step
图6(a)中爬楼轮椅和乘坐者整体的重心恰好位于F台阶沿的正上方,爬楼轮椅即将绕F台阶沿前倾。若履带底平面前端点(线)A与台阶沿F的距离小于台阶沿F和台阶沿E的距离,即FA<FE,此时发生前倾,履带会先支撑在E台阶沿所在台阶的水平面上,继续下行后履带再由台阶沿E支撑,此过程中爬楼轮椅俯仰波动较大,平稳性较差;若履带底平面的前端点(线)C与台阶沿F的距离大于台阶沿F和台阶沿E的距离,即FA>FE,此时发生前倾,履带底平面就能够直接支撑在台阶沿E上,爬楼轮椅爬楼平稳性最好。所以为了保证爬楼轮椅在爬楼过程中平稳性最好,要使 FA>FE,即有:
图6(b)中履带底平面后端点(线)C和H台阶沿处于临界接触状态,为了保证此状态之后爬楼轮椅能够由台阶沿F和台阶沿H支撑变成台阶沿E和台阶沿F支撑,此状态时重心B在水平面上投影的位置必须位于台阶沿F的左侧,即有:L2cos(δ-γ)>b (12)
图6(c)中履带底平面前端点(线)A和D台阶沿的水平面处于临界接触状态,为了保证爬楼轮椅不会在A点接触D台阶沿水平面之前发生前倾,此时重心B在水平面上投影的位置必须位于台阶沿 E 的右侧,即有:L1cos(β+γ1)>s1(13)
图6(d)中履带底平面后端点(线)C和F台阶沿的立面处于接触临界状态,为了保证爬楼轮椅不会在C点离开F台阶沿立面之后发生后仰,此时重心B在水平面上投影的位置必须位于台阶沿 E 的左侧,即有:L2cos(δ-γ)>b (14)
式(11)至式(14)联立化简之后得:
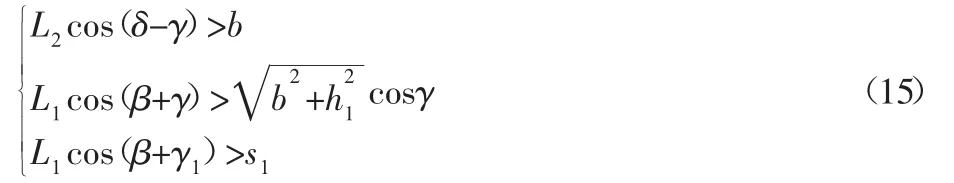
存在突高台阶的楼梯上需要满足均匀楼梯平稳性的要求,即满足式(1)和式(2),又要满足非均匀楼梯上楼过程和下楼过程中爬楼最平稳的平稳性要求,即满足式(10)和式(15),联立之后化简得:
由分析结果得:存在台阶突高时,将楼梯台阶的宽度、正常高度以及突高台阶高度参数代入式(16),若关系式成立,则该爬楼轮椅能够在此存在突高的非均匀楼梯上最平稳地上下楼。与台阶突高情况类似,台阶突低、突宽、突窄三种情况可以用相同的方法进行分析,可以分别得到一个参数代入式,将各项参数代入,若关系式成立,则该爬楼轮椅能够在非均匀楼梯上最平稳地上下楼。
4 样机试验
为了验证该基于行走轮摆动的履带变构式轮履复合爬楼轮椅在常见参数的住宅公共楼梯上能够满足爬楼平稳性要求,对爬楼轮椅在多个不同规格楼梯上进行样机试验[3],如图7所示,样机试验数据记录,如表1所示。采用在实验楼梯台阶上叠加木板的方法制造非均匀楼梯的实验条件,进行非均匀楼梯上平稳性样机试验,验证判断方法的可行性。实验数据记录,如表2所示。
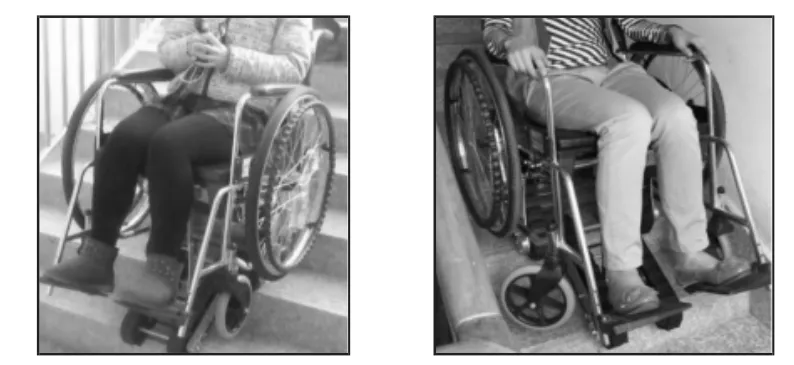
图7 爬楼平稳性样机试验Fig.7 Prototype Test of Climbing Stability

表1 均匀楼梯上爬楼平稳性样机试验数据Tab.1 Stability Prototype Test Data on Stairs with Uniform Step Size
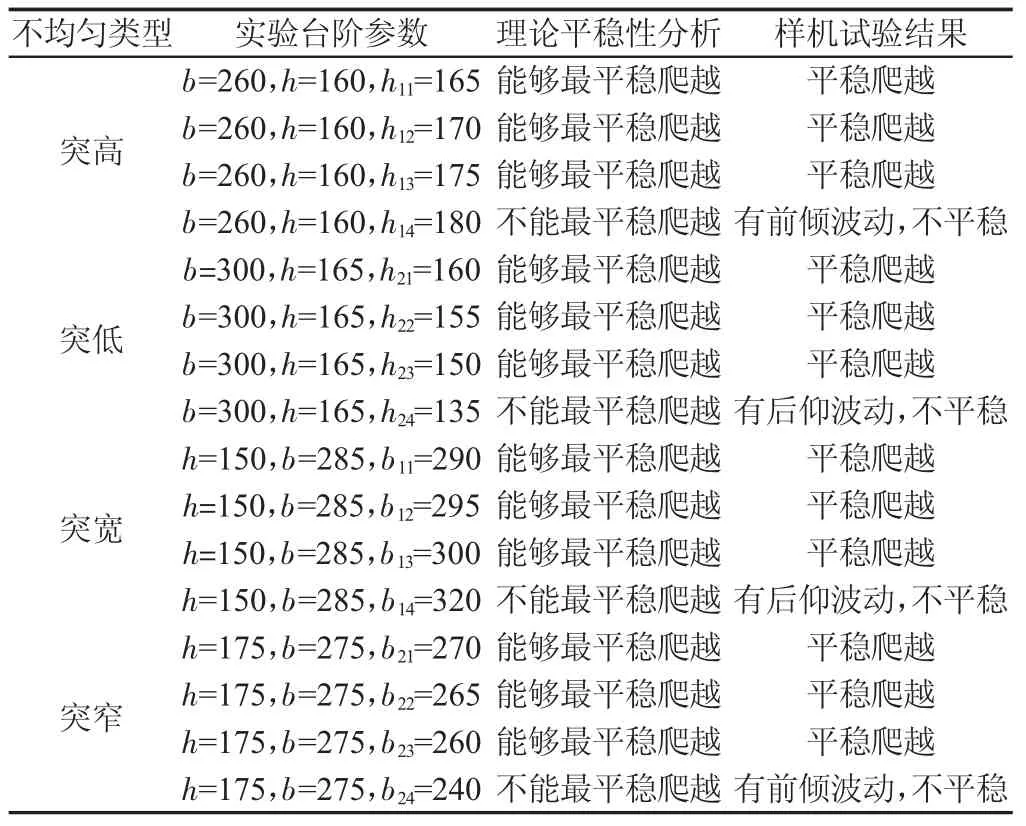
表2 非均匀楼梯上爬楼平稳性样机试验数据Tab.2 Stability Prototype Test Data on Stairs with Nonuniform Step Size
均匀楼梯上的样机试验结果表明,在常见台阶尺寸范围内的楼梯上,该爬楼轮椅楼能够平稳、安全地上下楼。爬楼轮椅爬楼过程中的平稳性受楼梯倾角的影响:当楼梯倾角γ<33.9°时,爬楼轮椅能够在乘坐者自操作下平稳、安全地上下楼;当楼梯倾角γ=33.9°时,爬楼轮椅略有波动。非均匀楼梯上的样机试验结果表明,爬楼轮椅在常见台阶尺寸参数范围内突变的台阶上,能够满足最平稳爬越某一突变台阶的平稳性要求;非均匀楼梯上平稳性分析得到的平稳性预判关系式,能够根据台阶参数进行爬楼轮椅平稳性预判,判断方法可行。
5 结论
对爬楼轮椅在均匀楼梯和存在某一台阶突高、突低、突宽或突窄的非均匀楼梯等几种不同楼梯上的履带爬楼过程进行爬楼平稳性分析,提供了一种在均匀楼梯以及非均匀楼梯上爬楼轮椅爬楼平稳性的分析方法。通过分析计算验证了该爬楼轮椅在现有的结构参数下对于常见尺寸的楼梯能够满足平稳性的要求,且总结出了非均匀楼梯上该爬楼轮椅的平稳性分析的一般规律。通过样机试验进一步验证了该爬楼轮椅能够满足常见台阶尺寸楼梯上的平稳性要求和非均匀楼梯上平稳性预判方法的可行性。
[1]李浩,侍才洪,康少华.轮履复合救援机器人的乘适性分析与优化[J].中国机械工程,2015,26(11):1444-1449.(Li Hao,Shi Cai-hong,Kang Shao-hua.Analysis and optimization of ride comfort for wheel-tracked rescue robot[J].China Mechanical Engineering,2015,26(11):1444-1449.)
[2]曹冲振,郭云东,周娜.轮履复合式安保机器人移动系统研究[J].机械设计与制造,2015(5):144-146.(Cao Chong-zhen,Guo Yun-dong,Zhou Na.Moving system research of wheel-tracked moving security robot[J].Machinery Design and Manufacture,2015(5):144-146.)
[3]曹冲振,周娜,王凤芹.履带变构式轮履复合爬楼轮椅设计[J].山东科技大学学报:自然科学版,2016,35(1):91-96.(Cao Chong-zhen,Zhou Na,Wang Feng-qin.Design of wheel-tracked stairwheelchairwithvariable-structuredtrack[J].JournalofShandongUniversity of Science and Technology:Natural Science,2016,35(1):91-96.)
[4]司跃元,赵新华,侍才洪.轮履复合机器人行走机构的设计及运动学分析[J].机械设计与制造,2013(7):191-193.(Si Yue-yuan,Zhao Xin-hua,Shi Cai-hong.Travelling mechanism design and kinematics analysis of wheel-tracked moving robot[J].Machinery Design and Manufacture,2013(7):191-193.)
[5]周玉兰,吴永超,马雍钧.自助爬楼轮椅的稳定性分析[J].中国康复医学杂志,2011(12):1144-1148.(Zhou Yu-lan,Wu Yong-chao,Ma Yong-jun.Stability analysis of selfhelp stair climbing wheelchair[J].Chinese Journal of Rehabilitation Medicine,2011(12):1144-1148.)
[6]王丽娟.行星滚轮转换步行式驱动爬楼梯轮椅设计[D].苏州:苏州大学,2010:16.(Wang Li-juan.The design of stair climbing wheelchair transforming driving between planets wheel and foot[D].Suzhou:Suzhou University,2010.)
[7]王建,谈英姿,许映秋.基于姿态的多关节履带机器人越障控制[J].东南大学学报:自然科学版,2011(S1):160-167.(Wang Jian,Tan Ying-zi,Xu Ying-qiu.Obstacle-navigation control method of multi-joint tracked robot based on robot pose[J].Journal of Southeast University:Natural Science Edition,2011(S1):160-167.)
