凸轮式恒力机构的设计

黄春强，赵 勇，刘 洋，姚 进

（四川大学 制造科学与工程学院 四川 成都 610065）

1 引言

恒力机构是一种在载荷产生位移时仍输出近似恒力的装置，因其不满足胡克定理，与传统的圆柱弹簧或其他弹性体有着本质的区别[1]，现已广泛用于机械、核工业、国防军事、仪器仪表等诸多需要恒力输出的领域，如电火花线切割机床、核电站管道、印刷机递纸机构等[2-4]。目前，获取恒力的方式主要包括通过恒力弹簧和恒力机构获取。文献[5]介绍了恒力弹簧的特性，并用大变形理论和椭圆积分工具对其进行设计分析，但恒力弹簧复杂的设计理论，限制了其使用范围，使得在实际应用中，通过恒力机构获取恒力的方式得到了更加广泛的应用。文献[6]设计了一种由曲柄滑块机构和弹簧组成的恒力机构，建立了该机构的恒力优化数学模型，对凸轮式恒力机构进行了优化以减小体积。文献[7]研究了软式操纵系统中的钢索张力调节器，通过合理选择张力调节器的参数，使得钢索张力的恒力范围尽可能地大。文献[8]研究了大尺度重型构件夹持机构的夹持力，建立了该机构的大尺度近恒力目标，利用循环程序与MATLAB软件对夹持机构进行了优化，使其尽可能大的范围保持恒力输出。文献[9]设计了一种基于弹簧-凸轮-转轮的恒力机构，通过弹簧-凸轮生成恒定力矩，恒定力矩通过转轮输出恒定力，通过数值求解的方法，求解出了凸轮的轮廓线。文献[10]设计了一种恒力弹性机构，其原理是通过设计传力构件的廓形，控制构件接触点法向，使机构内部力的传递方向与位移之间呈一定的函数关系，从而可以输出不随着位移变化的恒力，并通过数值解法，求解出内环截面的廓形曲线。如上所述的恒力机构，或者是结构不紧凑，或者是恒力范围小，或者是无法求得轮廓线方程的解析解。

针对以上不足，设计了一种凸轮式恒力机构，推导出了凸轮轮廓线的方程，并利用ADAMS进行动力学仿真，验证了该机构能在较大的范围内输出较精确的恒力。

2 结构设计与工作原理

凸轮式恒力机构的结构，如图1所示。凸轮式恒力机构的核心是凸轮机构，主要由凸轮、滚子、推杆、弹簧、螺钉和多个轴承组成。凸轮位于初始位置时，调节螺钉对弹簧施加一定的预紧力（预紧力的大小根据凸轮初始位置确定），弹簧通过推杆和滚子对凸轮施加压力，而压力作用线不经过凸轮中心，压力便会对凸轮中心产生力矩。凸轮转动时，弹簧的弹力随压缩量变化而变化，通过设计合理的凸轮轮廓线，让凸轮中心到压力作用线的力臂相应发生变化，使力与力臂的乘积保持恒定，从而获得恒力矩，恒定的力矩通过凸轮轴-转盘-钢丝绳对外输出恒定拉力。钢丝绳一端缠绕在转盘上，另一端连接需要牵引的外界物体上。为了减小摩擦力作用，推杆通过轴承进行约束。在外壳的下方设置一个底盘，一方面用来容纳螺钉，另一方面可以通过该底盘将整个机构固定在其他装置上。

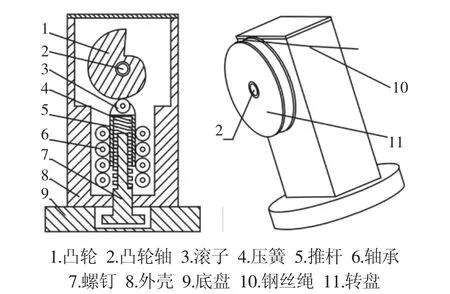
图1 凸轮式恒力机构结构图Fig.1 The Structure of the Cam Constant Force Mechanism

3 凸轮轮廓线的确定

3.1 凸轮轮廓线计算的分析与说明

如图2（a）所示，为了减小摩擦，凸轮式恒力机构使用的是滚子凸轮机构。由凸轮的相关理论可知，设计滚子凸轮机构的凸轮轮廓线时，为了方便分析和计算，可先将滚子中心A视为尖顶凸轮的顶尖，先计算出尖顶凸轮的顶尖的轮廓线（也就是滚子凸轮的理论轮廓线p-p），然后再以理论轮廓线p-p上一系列点为圆心，以滚子半径为半径，作一系列圆，再作此圆族的包络线便得到滚子凸轮的实际轮廓线q-q[11]。如图2（b）所示，凸轮式恒力机构实质是恒力矩机构，通过凸轮机构在凸轮轴上产生恒定的力矩T后，再通过半径为R的转盘输出恒力F，为了方便分析和计算，可以直接依据力矩恒定的约束推导出凸轮轮廓线的方程。

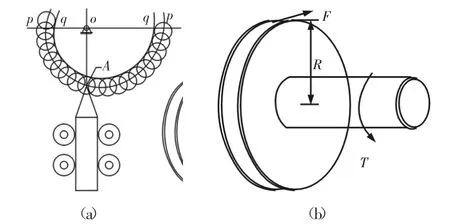
图2 凸轮的理论轮廓线与实际轮廓线和凸轮式恒力机构的恒力与恒力矩Fig.2 The Theoretical Profile Line and Actual Profile Line of the Camand the Constant Force and Constant Torque of the Cam Constant Force Mechanism

3.2 凸轮理论轮廓线的计算

如图3（a）所示，凸轮转到某一位置时，推杆顶尖A和凸轮的接触点切线为t-t，法线为n-n，此时，凸轮的受力情况，如图3（b）所示。推杆的受力情况，如图3（c）所示。在图3（b）中，对于凸轮，由凸轮中心点O力矩平衡，如式（1）所示。

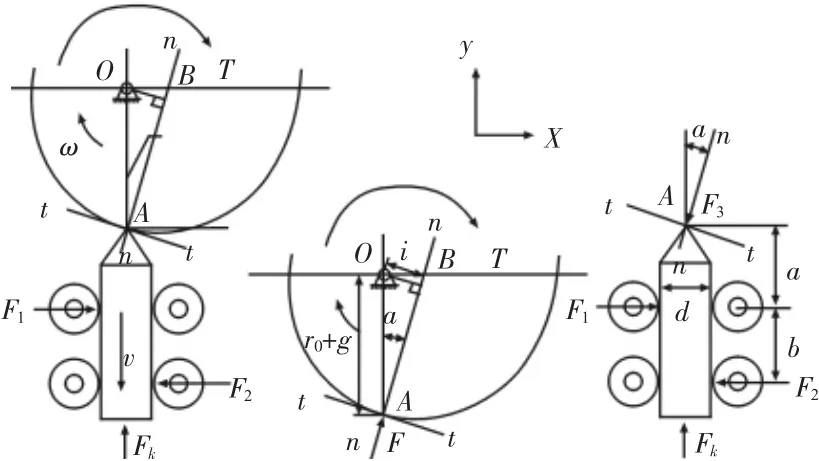
图3 凸轮式恒力机构的受力分析Fig.3 The Force Analysis of the Cam Constant Force Mechanism

式中：T—凸轮受到的外力矩，也是凸轮式恒力机构的输出力矩；F—推杆对凸轮的作用力；l—推杆对凸轮作用力的力臂；凸轮α—推杆中轴线与凸轮对推杆的力之间的夹角；r0—凸轮的基圆半径；s—推杆的位移，等于弹簧的压缩量。

由瞬心知识可知，B点为凸轮与推杆的相对速度瞬心，则：

式中：θ—凸轮转过的角度。

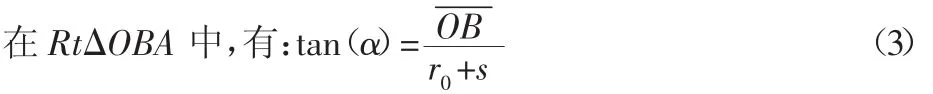
在图 3（c）中，对于推杆，由ΣFy=0，得 ：F3cos（α）-Fk＝0（4）

式中：F3—凸轮对推杆的作用力；Fk—弹簧对推杆的作用力。

式中：k—弹簧的刚度系数。

式中：C—常数。

为了简化计算，可令凸轮在转角为0时，推杆的位移为0，即θ＝0 时，s＝0，则有 C＝0。那么式（9）简化为：

根据凸轮相关知识，该凸轮理论轮廓线的极坐标方程为：

3.3 凸轮理论轮廓线范围的计算

由式（10）可知，该凸轮的理论轮廓线呈螺旋线形式，由里向外延伸。为使凸轮能够正常工作，还须确定出凸轮理论轮廓线的范围，也就是确定该螺旋线对应的角度θ的取值范围（θmin，θmax）。如图4所示，因为该凸轮为平面凸轮，θmax可直接取值为360°，而θmin与凸轮结构有关，需进行详细计算θmin。在Rt△AOB中，有：

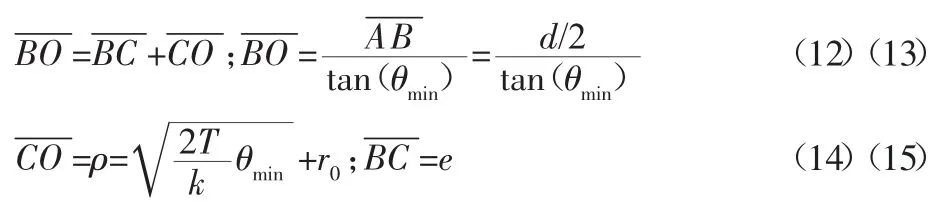
式中：e的值根据凸轮机构的结构设定，为已知。

联立式（12）～式（15），应用迭代法，可以求解出 θmin的值。进而有凸轮式恒力机构的恒力范围为S=r·（θmin-θmax）。

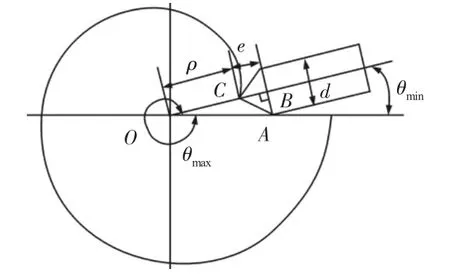
图4 凸轮理论轮廓线的范围Fig.4 The Range of the Theoretical Profile Line of the Cam

3.4 凸轮实际轮廓线的计算

如图5（a）所示，对于凸轮理论轮廓线上的任意一点A，如图式（16）所示。有式（16）即为凸轮理论轮廓线的直角坐标系方程。

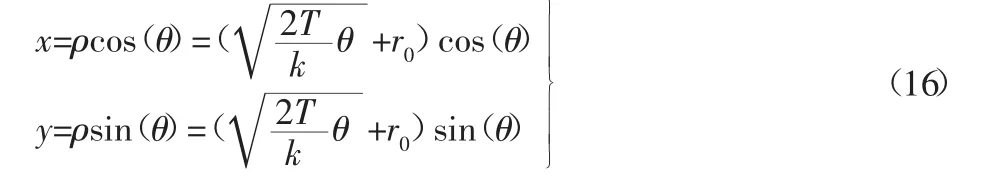
由凸轮相关知识可知，凸轮实际轮廓线与理论轮廓线在法线方向的距离等于滚子半径r，故对于凸轮理论轮廓线上的任意一点A（x，y），只要沿理论轮廓线在该点的法向距离为r，即得实际轮廓线上的对应点A′（x′，y′），如图5（b）所示，A′（x′，y′）的坐标为：

由高等数学知识可知，理论轮廓线A点处法线n-n的斜率（与切线斜率t-t互为负倒数）为：

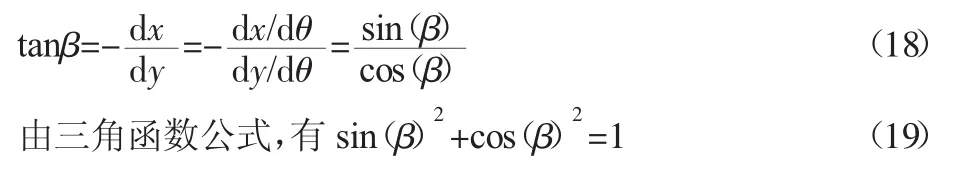
联立（18）（19）式，解得：

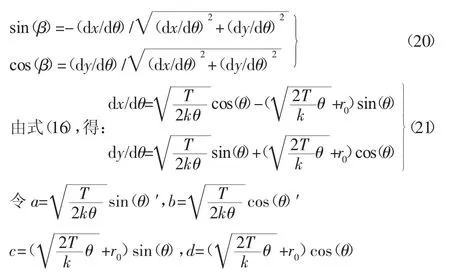
将式（21）代入式（20），可得：

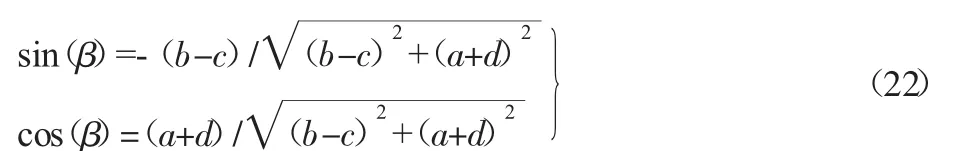
将式（22）代入式（17），可得：

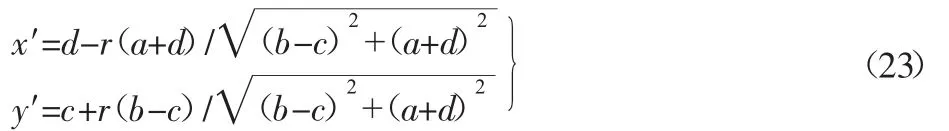
式（23）即为凸轮实际轮廓线的直角坐标系方程。

4 动力学仿真

为了验证上述理论计算，需建立仿真模型，并应用ADAMS软件来对其进行动力学仿真。根据上述的分析和计算可知，凸轮机构输出的恒力矩和整个恒力机构输出的恒力满足关系T=F·l，为了方便建模与仿真，可以通过验证凸轮机构能输出恒力矩来间接验证凸轮式恒力机构能输出恒力。

4.1 仿真模型的建立

将如图1所示的凸轮式恒力机构简化的仿真模型，如图6所示。为确定仿真模型结构尺寸，需给定相关的设计参数：设定所需的恒定力矩T为4000N·mm，弹簧的刚度系数k为24N/mm，基圆半径r0为18mm，滚子半径r取r0=9mm。将上述设计参数代入式（11）～式（16），式（23），最终得到凸轮的实际轮廓线，如图7所示。

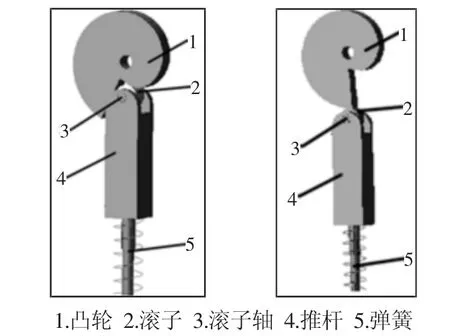
图6 凸轮式恒力机构的仿真模型Fig.6 Simulation Model of the Cam Constant Force Mechanism

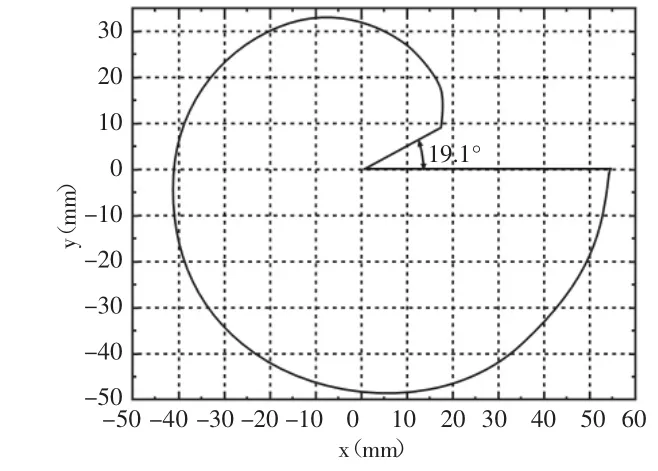
图7 凸轮的实际轮廓线Fig.7 The Actual Profile Line of the Cam

因为凸轮式恒力机构在实际使用时，载荷运动的速度较为缓慢，并且该恒力机构中凸轮的运动可以是与载荷作用的方向相同（顺时针方向），也可以是与载荷作用的方向相反（逆时针方向），为了使仿真与凸轮式恒力机构的实际工况相一致，仿真设置的凸轮转动速度为1d/s，对凸轮的驱动分为顺时针方向和逆时针方向两种情况。仿真模型的运动约束，如表1所示。力约束，如表2所示。当凸轮式恒力机构位于如图6（a）所示的初始位置时，推杆位于最高点，凸轮的角度θ为19.1°，由式（9）得弹簧的压缩量为s=10.5mm，则弹簧对应施加的预紧力为Fk=K·s=252.0N，对凸轮的施加顺时针方向的驱动，仿真时推杆向下运动。当凸轮式恒力机构位于如图6（b）所示的初始位置时，推杆位于最低点，凸轮的角度θ为360°时，由式（10）得弹簧的压缩量为s=45.8mm，则弹簧对应施加的预紧力为Fk=K·s=1099.2N，对凸轮的施加逆时针方向的驱动，仿真时推杆向上运动。对凸轮的转动副施加驱动进行仿真，具体的仿真参数如341°。

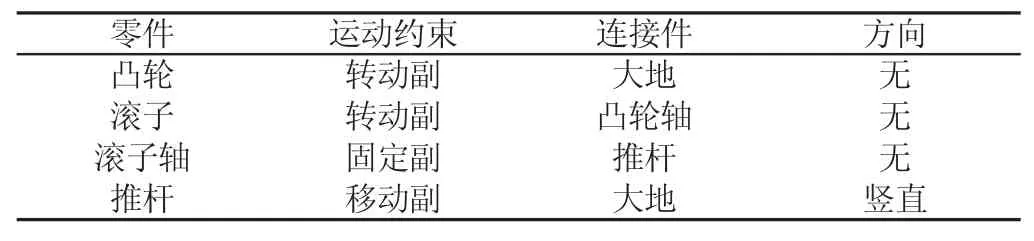
表1 模型的运动约束Tab.1 Kinematic Constraints of the Model

表2 模型的力约束Tab.2 Force Constraints of the Model

表3 模型的仿真参数Tab.3 Simulation Parameters of the Model

4.2 仿真结果分析

仿真后，测量到该仿真模型的输出力矩曲线，如图8所示。

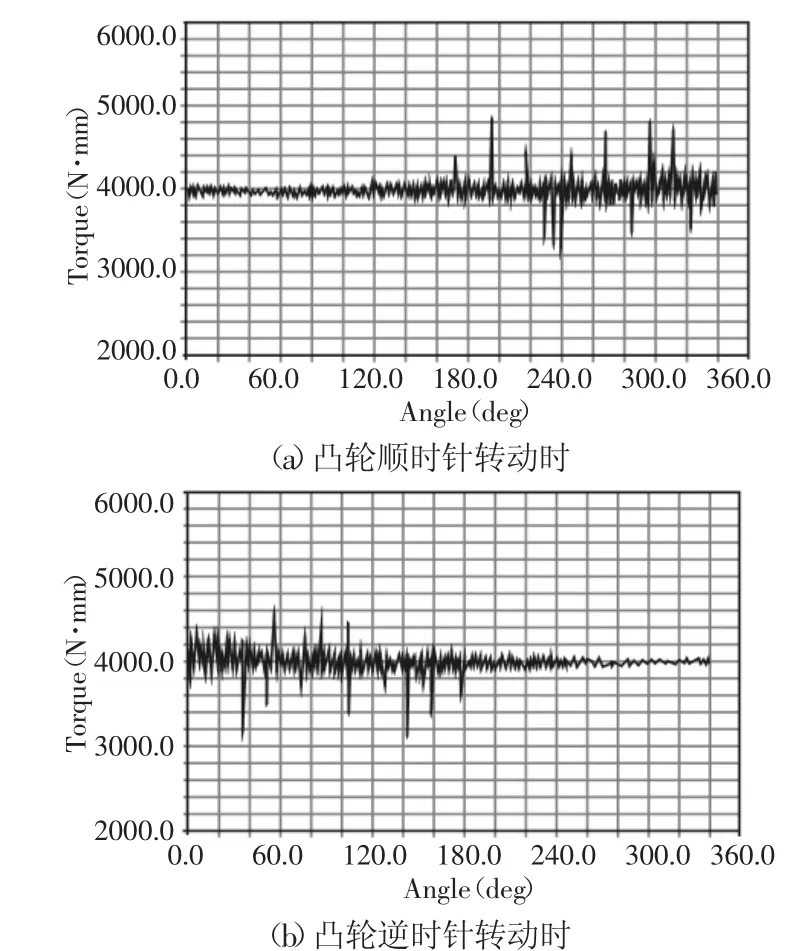
图8 模型的输出力矩曲线Fig.8 The Curve of Output Torque Curve of the Model

从图8可以得到：（1）无论凸轮顺时针转动还是逆时针转动，在较大的转角范围内（0～341）°，仿真模型的输出力矩的平均值均与所需的力矩近似相等；（2）仿真模型的输出力矩存在锯齿状的波动，这是因为在ADAMS中，仿真模型的凸轮轮廓曲线与滚子圆周线均是呈多段线的形式，而不是圆滑的曲线，同时由于凸轮与滚子在ADAMS中是呈刚体形式接触，两者接触时发生碰撞造成的；（3）仿真模型的输出力矩再某些时刻突然急剧增大或者减小，这是因为：根据输出力矩，由于凸轮受到的力与力臂在凸轮转动时因碰撞而不停地波动，当两者同时增大（或者减小）时，输出力矩便会突然急剧增大（或者减小）；（4）对比图 8（a）与图 8（b），仿真模型的输出力矩曲线存在较为明显的差异，这是因为在ADAMS中，凸轮轮廓的多段线节点密集度与轮廓的曲率相关，曲率越小，节点越密集，轮廓越圆滑，多段线越接近实际轮廓线，反之亦然。图8（a）中凸轮顺时针转动，随着转动角度的增大，凸轮轮廓的曲率增大，节点变稀疏，凸轮与滚子发生刚体碰撞的程度加重，输出力矩的波动增大。图8（b）中凸轮逆时针转动，随着转动角度的增大，凸轮轮廓的曲率减小，节点变密集，凸轮与滚子发生刚体碰撞的程度减轻，输出力矩的波动减小。综上所述，转盘半径一定时，该恒力机构能在较大的行程范围内输出较精确的恒力，进而验证了理论计算的正确性。

5 结论

基于力矩恒定原理，设计了一种主要由凸轮机构和转盘组成的凸轮式恒力机构，利用凸轮机构中的滚子对凸轮的压力与其力臂乘积保持恒定产生恒力矩，进而通过转盘转化为恒力输出。该恒力机构设计原理简单，结构紧凑；建立了凸轮式恒力机构的仿真模型，并利用ADAMS中进行动力学仿真，仿真结果表明，在误差允许的范围内，凸轮式恒力机构能在较大的范围内输出较精确的恒力，同时验证了理论计算的正确性；为今后研究恒力机构提供了有益的参考。

［1］Dhiraj Nahar，Thoms Sugar.Compliant constant-force mechanism with a variable output for micro/macro applications［C］.Proceedings of the 2003 IEEE International Conference on Robotics&Automation.Taibei Taiwan.2003：318-323.

［2］贾志新，滕向阳，陈剑.电火花线切割恒力张紧机构设计［J］.机械制造，2006，44（9）：49-51.（Jia Zhi-xin，Teng Xiang-yang，Chen Jian.Design of constant force tension mechanism wire-electrode cutting with electric spark，Machine Manufacturing，2006，44（9）：49-51.）

［3］冷真龙，杨金凤，宪臣.基于遗传算法的恒力吊优化设计［J］.机械设计与制造，2009，17（8）：53-55.（Leng Zhen-long，Yang Jin-feng，Xian-chen.Optimized design for constant force hanger based on genetic algorithm［J］Machinery Design ＆ Manufacture，2009，17（8）：53-55.）

［4］张海燕，赵亚鹏，张景霞.印刷机恒力机构大拉簧的优化设计［J］.包装工程，2008，29（2）：38-40.（Zhang Hai-yan，Zhao Ya-peng，Zhang Jing-xia Optimum Design of the big extension spring in the constant force mechanism of the printing press.packaging engineering，2008，29（2）：38-40.）

［5］Atsumi Ohtsuki，Shigemichi Ohshima.Analysis on characteristics of a C-shape constant-force spring with a guide［J］.JSME International Journal 2001，2（44）：494-499.

［6］李德军，刘洋.曲柄滑块恒力机构的设计［J］.机械设计与制造工程，2015，44（11）：54-56.（Li De-jun，Liu Yang.Design of slider-crank constant force mechanism［J］.Machine Design and Manufacturing Engineering，2015，44（11）：54-56.）

［7］丁文勇，孙秦.软式操纵系统中张力调节器的设计研究［J］.机械设计与制造，2006，9（8）：8-9.（Ding Wen-yong，Sun Qin.Study on the designing of cable tension regulator in the flexible airplane control system［J］.Machinery Design ＆ Manufacture，2006，9（8）：8-9.）

［8］王艾伦，刘云.大尺度重型构件夹持机构近恒力优化设计［J］.机械设计与制造，2008，12（4）：18-21.（Wang Ai-lun，Liu Yun.Design optimization of large range operating clampmachine of approximate constant force［J］.Machinery Design ＆ Manufacture 2008，12（4）：18-21.）

［9］严辉，李路明，郝红伟.一种恒力机构的设计与测试［J］.中国科技论文在线，2009，35（8）：550-554.（Yan Hui，LI Lu-ming，Hao Hong-wei，HU Chun-hua.Design and test ofa constant force generator［J］.Sciencepaper Online，2009，35（8）：550-554.）

［10］陈建，邓利娟.恒力弹性机构的设计［J］.中国机械工程，2010，45（16）：1944-1946.（Chen Jian，Deng Li-juan.Design of constant-force-elastic mechanism，China Mechanical Engineering，2010，45（16）：1944-1946.）

［11］孙桓，陈作模，葛文杰.机械原理［M］.北京：高等教育出版社，2006：161-162.（Sun Huan，Chen Zuo-mo，Ge Wen-jie.Theory of Machines and Mechanisms［M］.Beijing：Higher Education Press，2006：161-162.）