桁架支撑机翼布局客机的机翼质量计算

邢 宇，余雄庆

(南京航空航天大学航空宇航学院，江苏 南京 210016)

美国航空航天局(NASA)为未来的客机设定了这样一个目标：与现有客机相比，2030～2035年服役运营的客机其油耗要降低70%。为了实现这个目标，许多机构提出了各自未来的客机方案，其中一个引人注目的方案是波音公司提出的桁架支撑机翼(truss-braced wing，TBW)[1-2]布局客机。这种布局型式是在传统的客机机翼下方设置一个桁架，其特点是机翼具有大的展弦比、较小的后掠角、较薄的机翼厚度。大展弦比可显著减小诱导阻力；较小的后掠角易于实现层流机翼的设计，从而减少空气摩擦阻力；较薄的机翼厚度可进一步降低激波阻力。

这种客机布局型式引起了学术界和工业界的广泛重视。美国弗吉尼亚理工学院[3]对这种布局的设计参数进行了研究；法国航空航天研究院对这种布局进行了气动和结构方面的分析[4]；德国宇航中心对桁架支撑机翼布局的气动、载荷、结构、气弹之间的关系进行了研究[5]；中国商飞在考虑强度和气弹约束情况下，对桁架支撑机翼进行了结构优化[6]。

虽然这种布局型式在气动方面具有明显优势，但机翼结构质量仍然存在不确定性。与常规机翼相比，TBW布局的机翼质量是否增加还不清楚。为此，本文通过结构优化的方法来评估其质量。

1 研究对象

桁架支撑机翼布局客机概念飞机(765-095-TS1)是波音领导的“亚声速超绿色飞机研究”项目的最终方案[1-2]，能够满足NASA对下一代民航客机油耗的要求，可在小型机场起降。该概念飞机在NASA兰利研究中心的跨声速动力学风洞(TDT)中进行了试验[7]，根据实验结果，NASA和波音公司都认为该概念飞机的设计方案能够应用在下一代民航客机的设计上。本文以该概念飞机为研究对象，研究其机翼的质量特性。

概念飞机的机翼由主机翼和桁架部件(斜撑和支撑)组成，如图1所示，相应外形尺寸见表1。为防止斜撑和支撑屈曲导致质量增加，斜撑和支撑采用对称翼型NACA 0010，飞行中几乎不产生升力。斜撑与主机翼在58.7%展长处连接，支撑与主机翼在36.2%展长处连接，用于给主机翼卸载。主机翼采用相对厚度为11%的超临界翼型。

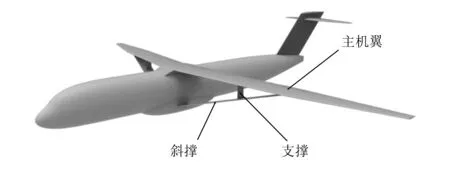
图1 桁架支撑机翼布局客机方案的外形

飞机最大起飞质量为63 500kg，巡航高度为44 000英尺(13 411m)，巡航速度为0.73倍马赫数，设计升力系数为0.775。

表1 桁架支撑机翼外形的主要尺寸

机翼结构布置方案如图2所示，主机翼和桁架采用翼盒结构。主机翼前梁位于弦长15%处，后梁位于弦长65%处，斜撑前梁位于弦长25%处，后梁位于弦长85%处，主机翼和斜撑的翼肋间距均为750mm。通过支撑将主机翼前梁与斜撑前梁连接，将主机翼后梁与斜撑后梁连接。

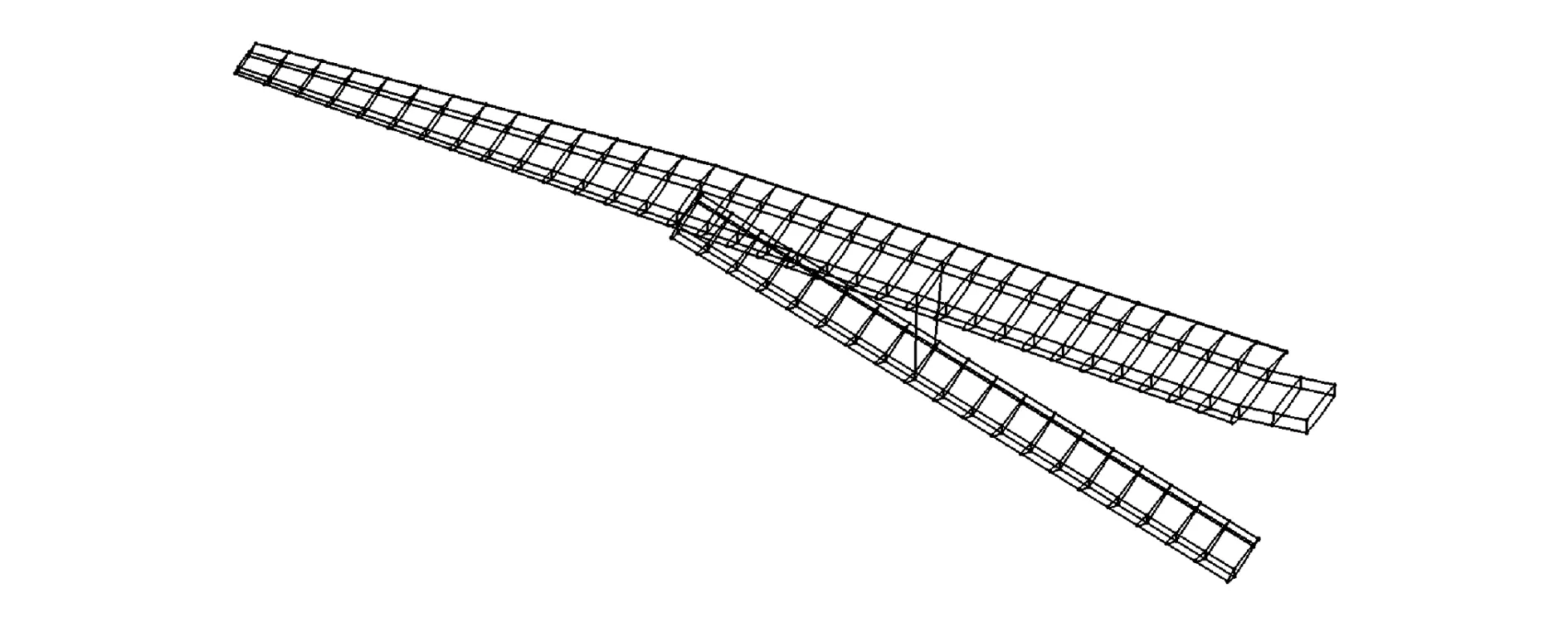
图2 桁架支撑机翼结构布置方案

本文以下要解决的问题是如何通过结构优化方法来确定结构尺寸，进而估算桁架支撑机翼结构质量。

2 桁架支撑机翼结构优化

采用基于结构有限元模型来进行结构尺寸优化设计。

2.1 有限元模型

根据图2所示的桁架支撑机翼结构布置方案，在结构分析软件MSC.Patran中建立桁架支撑机翼的有限元模型，如图3所示。

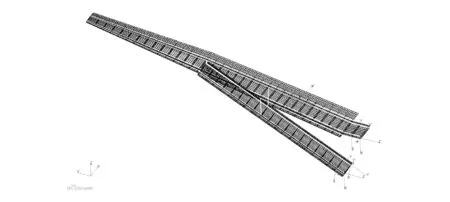
图3 结构有限元模型

蒙皮、梁腹板和翼肋采用shell单元模拟，梁缘条和支撑采用beam单元模拟。由蒙皮和桁条组成的加筋壁板采用等效平板的方法[8]，将加筋壁板等效为一块形状相同的无加强筋板，并使两板具有相同的力学性能。采用这种方法既能较准确地模拟各种桁条的力学特性，同时也避免了对桁条的有限元建模，可大大简化机翼结构有限元模型。

桁架支撑机翼结构的材料为T800碳纤维复合材料，其力学特性见表2，表中E1和E2为材料在1,2弹性主方向上的弹性模量，G12为剪切模量，ρ为密度，μ12为泊松比。

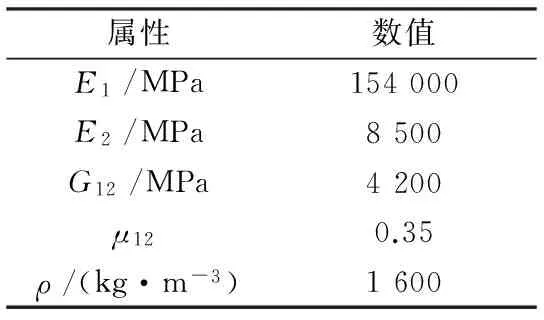
表2 碳纤维复合材料属性

对于约束处理问题，主机翼根部和斜撑根部均采用固支约束，支撑与机翼之间采用固支连接，支撑与斜撑之间采用铰支连接。

作用在机翼上的气动载荷采用BLWF程序[9]进行计算，该程序由俄罗斯中央气动院开发，可快速分析翼身组合体跨声速气动力。主机翼翼盒中装载50%的最大燃油质量[1-2]，并以分布质点的方式加入到结构模型中。过载情况为：最大正过载2.5g；最大负过载-1.0g。安全系数取1.5。

2.2 结构优化

桁架支撑机翼结构优化问题定义如下。

目标函数：翼盒结构质量最轻。

设计变量：1)蒙皮、梁腹板的厚度；2)梁缘条横截面积；3)支撑部件的横截面积。总的设计变量为96个，设计变量个数的组成详见表3。

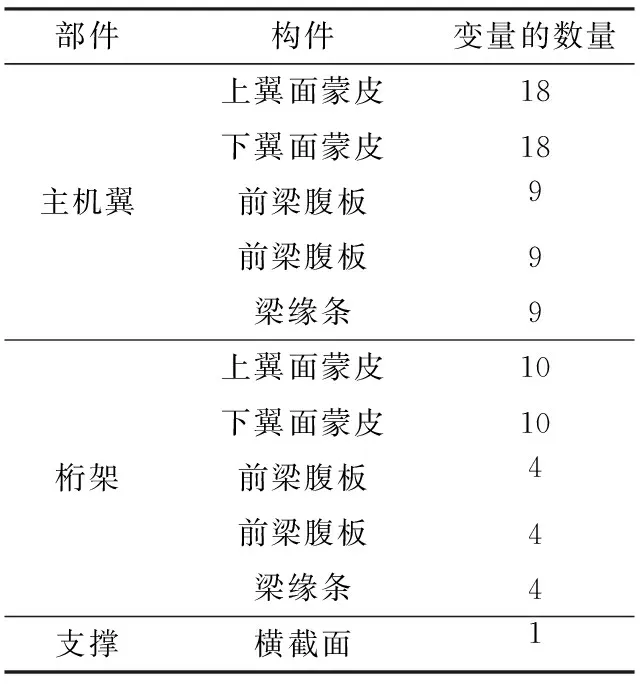
表3 设计变量的组成

约束条件：1)压应变≥-3 300με，拉应变≤4 500με；2)翼尖挠度≤10%展长；3)前6阶屈曲因子≥1.0。

结构优化计算在软件MSC.Nastran的设计灵敏度及优化分析模块(SOL 200)中完成。SOL 200是MSC.Nastran中专门开发的优化模块，可在考虑静力、模态、屈曲、瞬态响应、频率响应、气动弹性、颤振等约束情况下，对结构尺寸进行优化，并提供4种优化算法(修正可行方向法、序列二次规划法、序列线性规划法、罚函数法)供用户选用。本文采用序列二次规划法，该算法具有良好的收敛性和稳健性。

3 质量估算方法

机翼结构质量(Wwing)由4个部分组成，其组成表达式为：

Wwing=Wid+Wnid+Wrib+Wsec

(1)

式中：Wid为理想翼盒结构质量(承弯和承剪材料的质量)，通过第2节中结构优化方法获得；Wnid为非理想结构质量，包含了连接件、损伤容限、开口局部加强及发动机和起落架支持结构的修正质量，叠加前面3项质量后，得到修正后主承力结构质量；Wrib为翼肋质量；Wsec为次结构质量，主要包含前后缘结构、襟副翼、绕流片、增升装置、翼尖等质量。由式(1)并采用文献[10]给出的修正公式，可计算出整个机翼的质量。

4 结果和分析

基于上述结构优化方法和质量估算方法，获得桁架支撑机翼结构各部分的质量，计算结果见表4。整个桁架支撑机翼质量为8 390kg。由于飞机最大起飞质量为63 500kg，因此桁架支撑机翼质量占飞机最大起飞质量(全机质量)的13.2%。

表4 优化后各部件质量

为了进一步分析机翼结构的受力情况，图4给出了机翼的应变云图，图5给出了机翼的屈曲云图。从图4和图5可以看出，相比于常规布局客机，桁架支撑机翼的最大应变处和发生屈曲处均位于桁架与机翼的连接处。在优化计算过程中，连接处的应变值首先达到约束边界。从优化结果中还可看出，主机翼的尺寸主要由应力约束决定，桁架的尺寸主要由屈曲约束决定。

图4 优化后的机翼结构应变云图

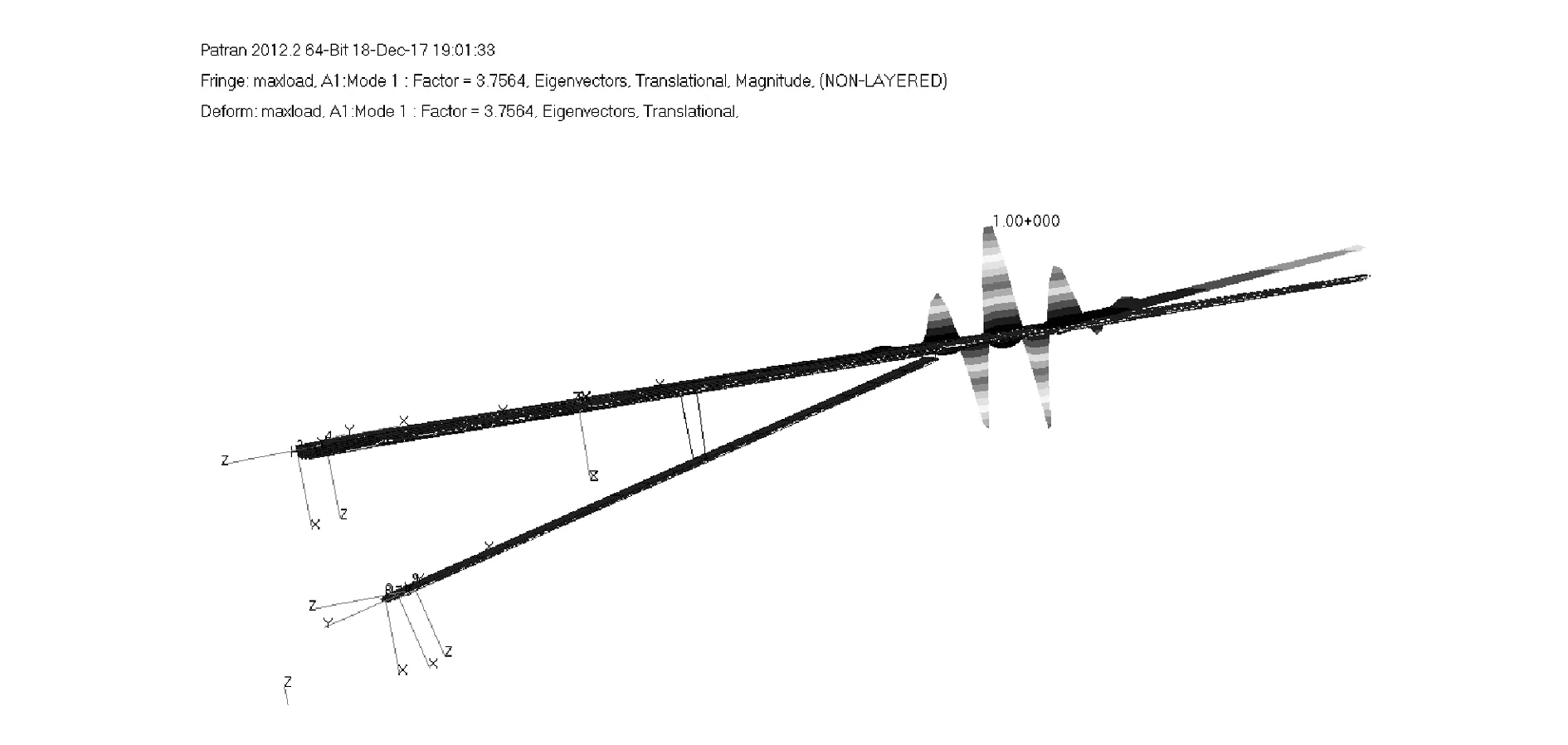
图5 优化后的机翼结构屈曲云图

图6给出了优化后主机翼上表面的蒙皮厚度分布，图7给出了优化后主机翼下表面的蒙皮厚度分布。在主机翼与斜撑连接处，蒙皮厚度最厚。

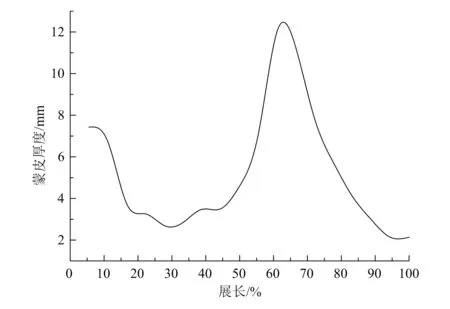
图6 优化后主机翼上表面蒙皮厚度分布

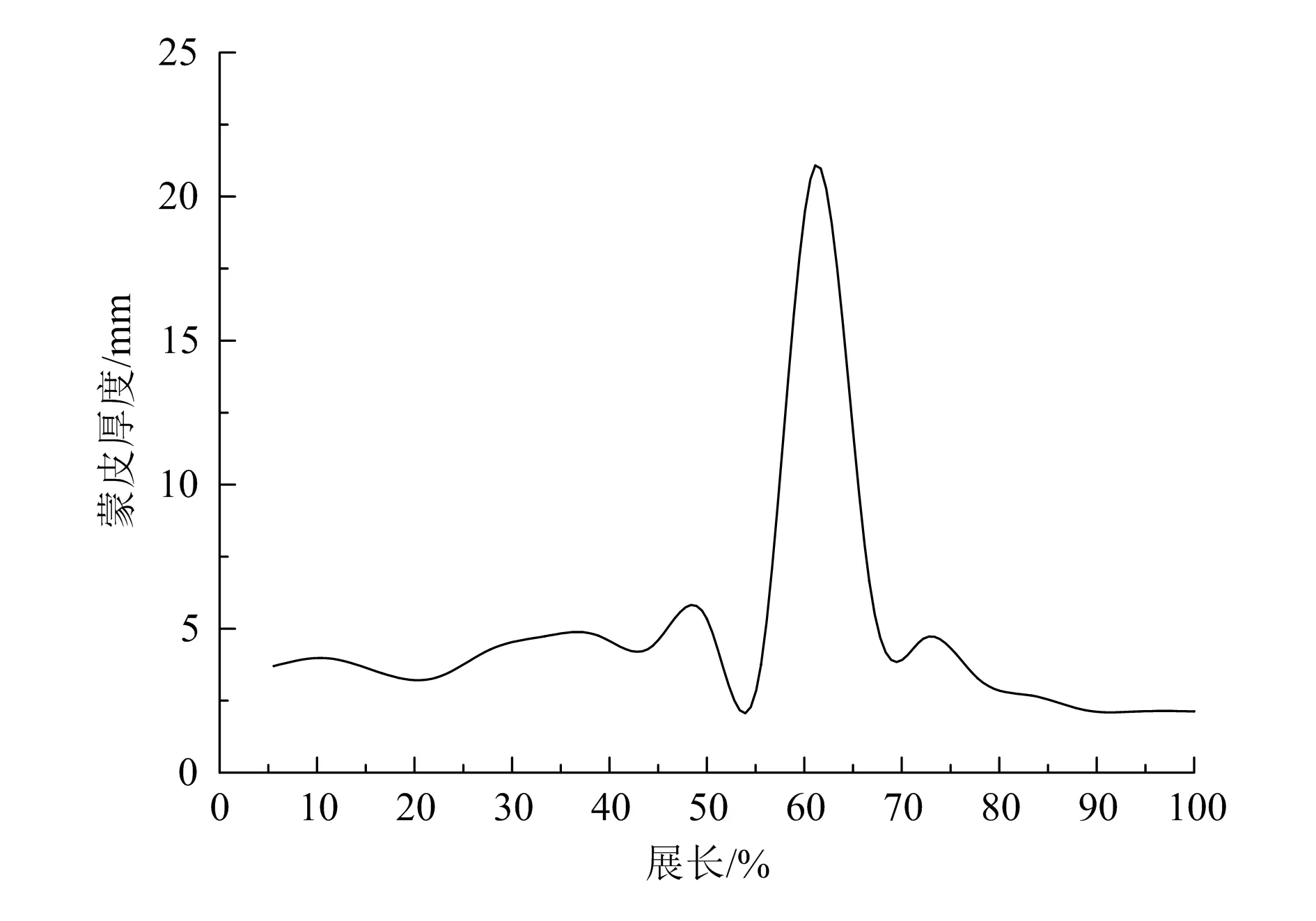
图7 优化后主机翼下表面蒙皮厚度分布

5 结论

针对桁架支撑机翼布局客机的机翼质量计算问题，本文以典型的桁架支撑机翼布局客机为研究对象，基于结构有限元分析方法和结构优化方法对桁架支撑机翼结构尺寸进行了优化设计，在此基础上对桁架支撑机翼结构质量进行了估算。研究结果表明：

1)桁架支撑机翼质量占全机质量(最大起飞质量)的13.2%，而常规布局客机的机翼结构质量通常占全机质量(最大起飞质量)的9%～14%，因此桁架支撑机翼质量在全机质量中的占比与常规机翼质量的占比相当。

2)桁架支撑机翼的最大应变和发生屈曲处均位于桁架与主机翼连接处。

3)主机翼的结构尺寸主要由应变约束决定，桁架的结构尺寸主要由屈曲约束决定。

需要说明的是，本文未考虑机翼颤振约束对机翼结构质量的影响，在后续研究中将考虑这一因素。

[1] BRADLEY M K, DRONEY C K. Subsonic ultra green aircraft research phase I: final report[R]. Washington, US: NASA/CR-2011-216947, 2011.

[2] BRADLEY M K, DRONEY C K. Subsonic ultra green aircraft research phase Ⅱ:n+4 advanced concept development[R]. Washington, US: NASA/CR-2012-217556, 2012.

[3] MEADOWS N A, SCHETZ J A, KAPANIA R K, et al. Multidisciplinary design optimization of medium-range transonic truss-braced wing transport aircraft[J]. Journal of Aircraft, 2015, 49(6):1844-1856.

[4] CARRIER G, ATINAULT O, DEQUAND S, et al. Investigation of a strut-braced wing configuration for future commercial transport[C]//Proceedings of 28th International Congress of the Aeronautical Sciences. Bonn: ICAS, 2012:1-16.

[5] MOERLAND E, PFEIFFER T, BÖHNKE D, et al. On the design of a strut-braced wing configuration in a collaborative design environment[R]. Reston, US: AIAA-2017-4397, 2017.

[6] WANG G, ZENG J, LEE J D, et al. Preliminary design of a truss-braced natural laminar flow composite wing via aeroelastic tailoring[J]. Journal of Aeroelasticity and Structural Dynamics, 2015, 3(3):1-17.

[7] SCOTT R C, BARTELS R E, FUNK C J, et al. Aeroservoelastic test of the subsonic ultra-green aircraft research truss-braced wing model[J]. Journal of Guidance Control and Dynamics, 2016, 39(8):1-14.

[8] 余雄庆,欧阳星,邢宇,等. 机翼结构重量预测的多学科分析优化方法[J]. 航空学报, 2016, 37(1):235-243.

[9] 党铁红. 俄罗斯中央空气流体动力研究院(TsAGI)在亚音速飞机巡航构型空气动力设计数值计算方法方面的进展[J]. 民用飞机设计与研究, 2006，82(3):14-22.

[10] TORENBEEK E. Advanced Aircraft Design: Conceptual Design, Analysis and Optimization of Subsonic Civil Airplanes[M]. Chichester, United Kingtom: John Wiley & Sons Ltd, 2013.