网络相关性、结构与系统性金融风险的关系研究
2018-03-05胡宗义黄岩渠喻采平
胡宗义,黄岩渠,2,喻采平
(1.湖南大学 金融与统计学院,湖南 长沙 410006 ; 2.中国人民银行长沙中心支行, 湖南 长沙 410005;3.长沙理工大学 经济与管理学院,湖南 长沙 410076)
一、引言
我国经济已经由高速增长阶段转变到高质量发展阶段,转变发展方式,优化经济结构,转换增长动力是当前的重要任务。金融系统作为现代经济系统的功能核心,也需要完成质量、效率与动力的变革,服务好实体经济,使金融经济的增长更稳健,风险更可控。从系统论的观点看,系统的稳定性与各组成部分之间的联系和系统结构有关,研究表明系统性金融风险也与金融机构的相关性及金融网络结构直接关联。深化金融系统改革,服务好实体经济,可以降低金融机构相关性,优化系统结构,从而达到有效降低系统性金融风险的目的。
国内外在系统性风险测量的研究方面主要包含网络分析法、尾部度量法、或有权益分析法以及宏观压力测试法四类[1]。网络分析研究是最近系统性金融风险的热点[2],研究表明网络关联性与系统性风险之间不是单调关系,但关联性处在高位时,外部冲击会给系统带来更大的损失。在网络结构方面,已有文献主要在不同的网络结构下研究金融系统的传染性、系统性风险大小等,提出利用资本管理、流动性管理来调整网络结构,从而干预系统性风险。
二、文献回顾
在网络分析研究方面,Allen等人[3]基于DD模型分析了流动性与网络关联度,发现分散风险和增加关联度可以降低系统性风险。Iori等人[4]分析了风险分散与系统性风险的关系,认为网络关联度与系统性风险之间没有单调性关系存在。Stiglitz[5]认为分散风险和传染性增加是一体的,关联性增加使风险分散,但增强了大冲击下的传染性。Gai等人[6]利用数值模拟方法证明,当关联程度低时,传染发生频率低破坏性小,当关联程度高时,传染更容易发生破坏性大。苟文均[7]通过CCA模型证实债务杠杆增加了系统性风险的生成和传染。唐文进[8]研究了极端事件对系统性风险的影响并提升了预测能力。郑振龙[9]利用平均相关系数对股票、债券市场进行了研究,发现平均相关系数反映了系统性风险。对金融网络建模时,一般采用银行间存贷数据、支付数据、CDS数据、风险敞口数据等单一数据,而银行间的相关性关系是多维度的。Thrner等人[10]指出在金融网络中银行间市场是很重要的,但担保市场和信用派生市场在放大波动方面也有非常重要的作用。Bargigli等人[11]以墨西哥银行数据构建了多层次网络,发现不同层的网络结构是不一样的。Poledna等人[12]进一步利用墨西哥银行的相互存款、交叉持有债券、派生产品和外汇研究了系统性风险。方意[13]研究了四类传染渠道,发现杠杆渠道和负债违约渠道对系统性风险的影响更为重要。本文采用唐文进[8]、郑振龙[9]、Acharya等[14]、Chen等[15]文献中采用的上市金融机构数据测度网络相关性。
在网络结构的研究方面,Mantegna[16]研究了机构之间的Pearson相关系数,认为相关性大的机构不仅受经济政策的影响,也受产业政策的影响,而相关性小机构的主要受经济政策的影响。Vladimir[17]利用美国股市数据证明了在交叉相关系数大于0.2时,网络是无标度网络。Brusco[18]建立了一个考虑道德因素的模型,得出了完全网络结构比不完全结构更容易引发金融危机的结论。Castiglionesi[19]研究了网络效率与分散风险能力,得出最优网络结构为中心外围式网络结构。Lenzu等人[20]通过随机冲击试验结果表明随机网络比无标度网络更稳定。隋聪[21-22]的研究表明网络集中度越高,传染的可能性越小但传染损失越大。邓超[23]研究发现中心外围式网络比无标度网络更容易造成传染,但金融困境时恢复力更强。
在网络相关性方面,文献大多采用Pearson相关系数、交叉相关系数。Kritzman等人[24]采用相关系数矩阵的特征值,郑振龙[9]、Kolanovic等人[25]采用平均相关系数,Engle等人[26]采用交叉相关系数的平均值。由于Pearson相关系数只适合测度线性相关,本文构造互信息系数来衡量网络相关性,互信息系数相对Pearson系数来说,一是可以度量非线性相关,二是不需要计算相关的参数,比Pearson系数测量相关性更稳定。
三、基于互信息的网络关联模型
(一)建立互信息相关系数矩阵的时间序列
Rothman[27]研究了经济领域时间序列中非线性相关与处理,金融变量非线性相关广泛存在,在很多情况下,采用Pearson相关系数、交叉相关系数等来计算金融变量之间的相关性是不适宜的。Dionisio等人[28]构造了X,Y的关系为一个增加扰动的余弦波函数(X,Y强相关),计算得出Pearson相关系数为0,Rank相关系数为0,互信息系数为0.91,证实互信息不仅能测量线性相关,也能测量非线性相关关系。本文采用互信息系数来计算相关性,预期比Pearson相关系数,交叉相关系数更稳定。
X为随机变量,PX(x)为X的概率密度函数,X的信息熵H(X)定义为:
(1)
Y是另外一个随机变量,概率密度函数为PY(y),X,Y的联合分布密度函数为PXY(x,y),联合熵H(X,Y)定义为:
H(X,Y)=-∬PXY(x,y)log(PXY(x,y))dxdy
(2)
X发生情况下Y发生的条件熵H(Y|X)定义为:
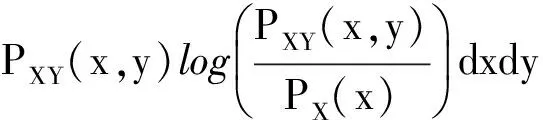
(3)
X,Y的互信息I(X,Y)定义为:
I(X,Y)=H(X)-H(Y|X)=H(Y)-H(X|Y)=H(X)+H(Y)-H(X,Y)
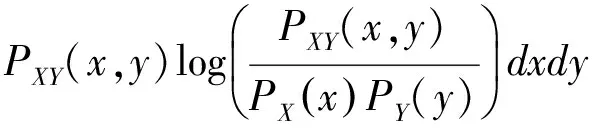
(4)

(5)
通过(5)式计算互信息系数,X,Y之间不相关时,由于I(X,Y)=0,相关系数为0;X,Y之间有函数关系时,相关系数为1。上式较好地描述了X,Y之间的相关关系。我们通过(4),(5)计算金融机构的互信息系数矩阵时间序列,以每个时点的相关系数矩阵为邻接矩阵,我们建立起金融网络的时间序列,该网络随着时间变化不断变化。
金融网络可以用图来表示,图的数学表达式为:G=(V,E),由顶点集合V(v)和边集合E(e)组成。其中V是顶点的集合,E是边的集合。本文中考虑的金融机构之间的相关性关系,顶点为金融机构,顶点的值为金融机构的总市值,边为金融机构之间相关性,值为金融机构之间的互信息相关系数,由于互信息相关系数是对称的,本文中金融机构网络为无向图。
(二)网络相关性与系统性风险
本文使用机构的每日总市值来测度金融机构的相关性,主要依据是因为资产小于等于负债是多数文献对金融机构倒闭的假定,资产与负债之差是机构的所有者权益,而所有者权益的市场价值对上市公司来说是公司的总市值。相对股价来说总市值考虑了机构规模,机构分红与扩股,采用总市值比股市价格更具备合理性。本文采用总市值来计算金融机构之间的相关性,认为这种相关性已经包含了金融机构的直接相关性与间接相关性。
在计算相关系数时遵从Engle等人[26]动态等相关模型(DECO)关于机构间一天内的相关系数不变的假设,相关系数随着日期变化,并采用网络对手相关系数的均值来计算整个网络的相关性,计算方式为:
(6)
其中v为某一时点的网络相关性,xij为第i个机构与第j个机构的相关系数,n为机构总数量。通过(6)式,我们计算出每个时点的网络相关性,得到网络相关性的时间序列。
在系统性风险测量上,我们采用金融指数表示。从直观上看指数越大,系统性风险越高。我们假定从长期看金融系统的总市值满足一个固定的概率分布,X是将来可能的损失,用VaRα(X)表示系统性风险的大小,VaRα(X)=-inf{x|P(X≥x)≥1-α}。我们固定α时,因为总市值满足一个固定的概率分布,将来可能的损失只与当前的总市值相关,当前的总市值越高,将来可能遭受的损失越大。实际上可以证明,只要系统性风险测量方法(如VAR,ES等)满足风险一致性测量中的平移原理[31],即ρ(x+a)=ρ(x)-a,就可以用指数曲线近似代替风险曲线。因为如果在指数为α点测到的风险为ρ(x),在满足平移原理的情况下,在指数为β的点测到的风险一定为ρ(x)+λ(β-α),λ(β-α)是系统风险损失准备金(其中λ为常数)。系统性风险曲线是系统指数曲线在y轴平移距离ρ(x)后再放大λ倍的结果。当前交易商流行的计算指数期货的保证金算法,就是以指数为基准计算。
本文实证中通过网络相关性时间序列与指数时间序列的比较来分析相关性与系统性风险的关系。通过x1>x2(x1,x2的值为各时点网络相关性)时,是否有f(x1)>f(x2),f(x1),f(x2)的值为各时点的金融指数,以此判断网络相关性与系统性风险之间是否有单调关系。
(三)网络结构与系统性风险
以相关系数矩阵为邻接矩阵的网络是全连通网络。为了研究网络结构,需要对网络进行压缩。本文采用Vladimir等人[17]等文献中的假设,即在外部冲击下,相关性小的部分对系统性风险的影响可以忽略,本文采用两种方式压缩,一是保持连通性下的相关性压缩,即压缩为最大生成树;二是完全基于相关性的压缩。
1.基于最大生成树的压缩。使用最大生成树进行压缩是为了展示网络总体结构。最大生成树数学表示为:GT=(VT,ET),由于本文中G是全连通的图,我们寻找的最大生成树顶点数与原图一样,有VT=V我们定义图G上边的一个函数f(e)为:

2.基于相关性的压缩。使用相关性压缩的目的是研究网络内部结构与内部相关性,本文中使用θ=0.7压缩,具体做法是将相关性小于阀值的边从全连通图中移除,可以证明压缩后的网络为无标度网络。也可以采用其他阀值,阀值的大小不影响本文的结论。
我们使用网络偏心距判别网络结构与系统性风险之间的趋势性关系。网络中节点之间的距离定义为两个节点最小的边的数目,节点的偏心距定义为节点到图中所有节点的距离的最大值。网络偏心距定义为网络中最小的节点偏心距,网络平均偏心距定义为网络中所有节点的平均偏心距。平均偏心距实际上是网络集中度的一种量度。从偏心距的定义可以看出,偏心距越小,越接近中心外围式网络,偏心距最小的节点为网络的中心。本文利用网络偏心距描述网络结构,并将偏心距用在最大生成树、相关性压缩的网络中。我们通过网络偏心距来判断网络的集中度,偏心距越小,认为网络越呈现为中心外围式结构,偏心距大时,呈线性结构或松散结构。
本文分别计算各时点最大生成树、相关性压缩网络的偏心距,形成偏心距时间序列,通过偏心距曲线与指数曲线的对比,判断网络结构与系统性风险是否有趋势性关系。
(四)网络内部相关性与系统性风险
本文用最大团方法挖掘网络中联系最紧的小团体,分析形成最大团的原因,提出干预系统性风险的方法。最大团是图中最大的全连通子图,最大团的含义是机构中联系最紧密的团体。由于最大团中的个体相关性强,个体会对整个团产生比较显著的影响。
(五)数据与计算方法
本文数据获取自国泰安数据库。考虑到2015年的股灾和2016年初的股灾,选取时间段为2014-2016年。剔除2015年以后上市的机构后,银行类机构总计16家,证券类机构24家,保险类机构6家,其他类机构7家,实际53家金融机构列入计算。首先利用每日机构总市值数据计算金融机构之间的互信息(R软件中infoeth软件包,版本号1.2.0),使用互信息建立互信息矩阵时间序列,再计算基于互信息的系数矩阵时间序列;然后利用系数矩阵构造最大生成树与相关性网络;最后计算最大生成树与相关性网络的偏心距(Eccentricity)并研究网络相关性、结构与系统性风险的关系。结合互信息计算要求与我国证券市场波动的频率,本文选择125个数据为一个滑动窗口来计算。
四、实证结论与分析
为了统计方便,机构代码以字母标示,银行类机构以Y开头,保险类机构以B开头,证券类机构以Z开头,其他金融机构以Q开头,代码数据在后文的实证分析中使用,机构类数据如下表:
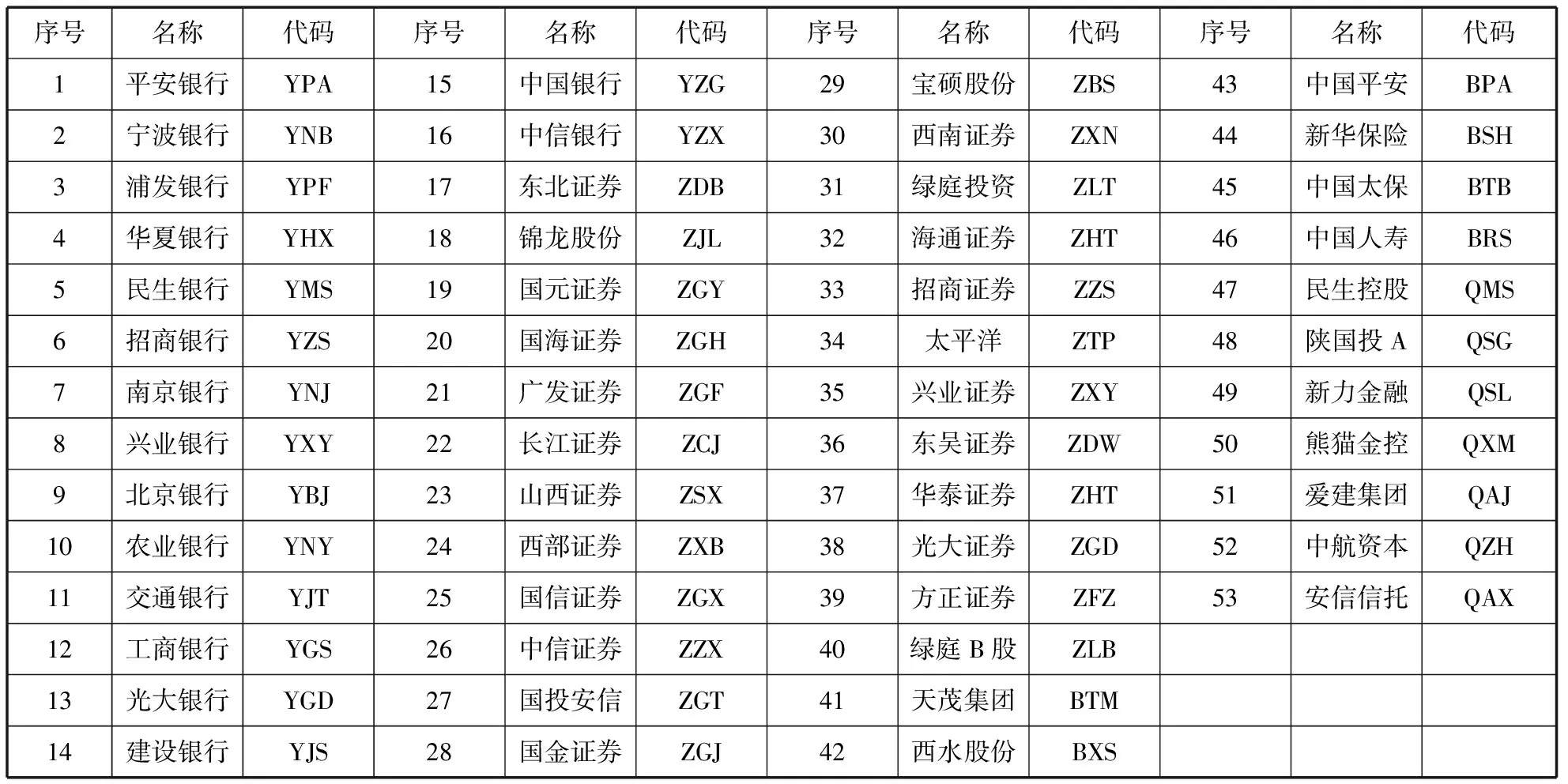
表1 金融机构代码表
我们使用平均相关系数法对系统性风险作预测,图1中a是平均互信息系数序列与金融指数的叠加,b是平均Pearson系数时间序列与金融指数的叠加。为了比较方便,我们将基期(2014年7月8日)的互信息系数与相关系数设置为100。
互信息系数表示的是金融机构个体之间的相关程度,平均互信息系数表示金融机构整体的内部相关程度。从图1 a我们发现,平均互信息相关系数增强时,一般情况下指数也增大,但相关性增加总是先于指数到达高点,网络相关性高点发生在风险发生前。我们发现在部分时段,网络相关性与金融指数之间的关系不是单调的,例如2014年11月17日至2015年12月2日,相关性从x1=0.5536959降低到x2=0.4627035,而指数从f(x1)=113.4497上升到f(x2)=140.1508。在x1
2015年我国系统性金融风险主要是金融杠杆造成的,在金融指数的上涨期(2015年6月8日前),金融机构间的相关性增加,系统性风险增加,在2015年4月30日互信息到达高点后,最后一轮的上涨,金融机构之间的相关性并没有增强,而是开始回落,经济学的解释是市值的上涨已经不是普涨,而是出现了分化,相关性开始降低,这可以从各机构市值曲线图中得到验证。在金融指数的下跌期(2015年6月8日后),机构间的平均相关性同步回落,指数下跌与相关性基本同时到达低点。最低点过后,机构之间的相关性开始增强,系统吸收风险,金融指数出现上涨。
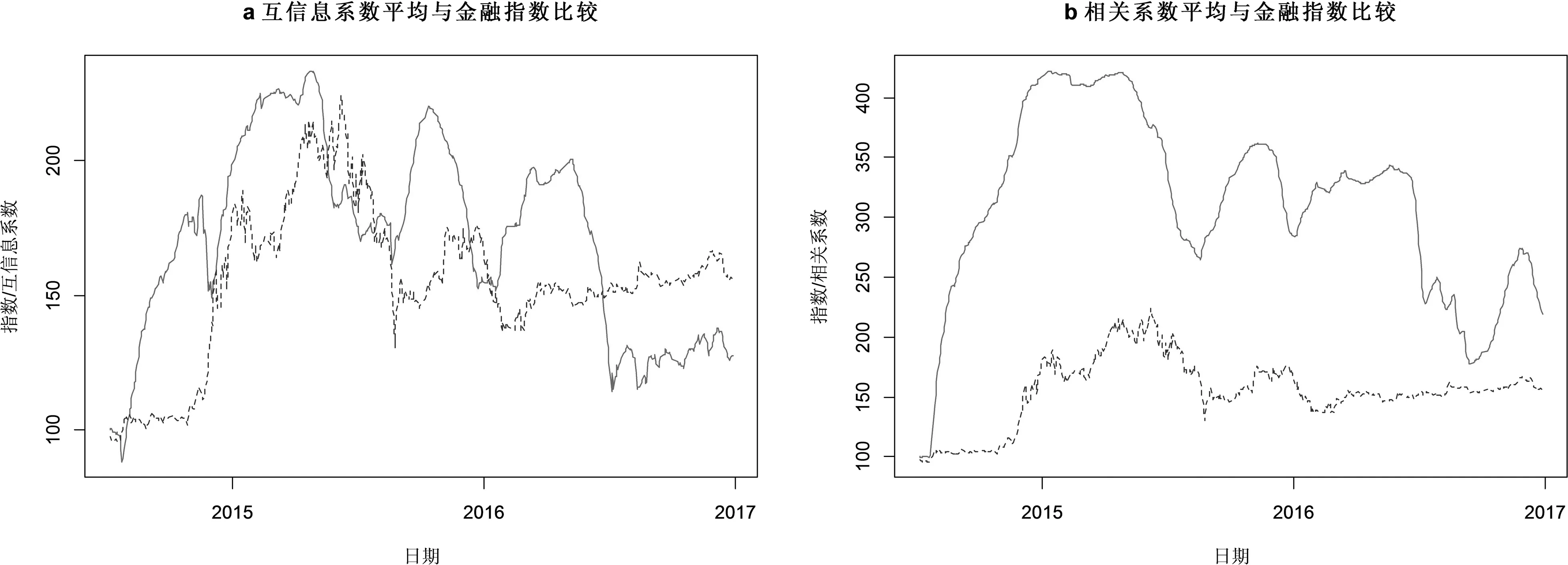
图1 互信息系数平均、相关系数平均与指数比较图
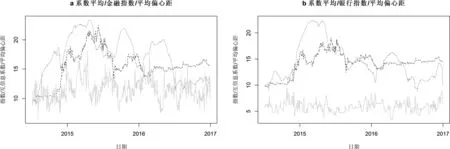
图2 互信息系数平均、指数与偏心距
从图1 a可以看到基于互信息的相关系数曲线较好地与指数曲线吻合。由于上涨最后阶段总是存在一个阶段的分化期,基于互信息的相关系数总是能提前回落,所以能够较好地预测风险,在2015年4月30日互信息到达高点后,金融指数2015年6月8日才到达最高点,每一次金融指数的上涨,互信息相关系数都提前到达高点然后回落。基于互信息系数的相关性对指数的涨跌更为清晰,而图1 b基于Pearson相关系数的时间序列预测性不是很理想,可能原因是机构之间的部分相关性是非线性的。
为了比较各时期网络结构,本文将网络压缩形成最大生成树,并计算每棵生成树的偏心距,并采用平均偏心距作为网络结构的特性。图2分别是2014年7月8日至2016年12月31日金融系统平均偏心距、金融系统互信息系数与金融指数,银行系统平均偏心距、银行系统互信息系数与银行指数叠加,为了便于观察,平均偏心距、相关性、金融指数的初期数值定义为10以便比较。图2 a,实线是金融平均偏心距,点划线是金融指数。图2 b,实线是银行平均偏心距,点划线是银行指数。
我们从图2可以看到,不管是金融系统还是银行系统,在外部冲击的作用下,网络结构发生周期性震荡。金融系统的网络结构比银行系统网络结构变化更大,这不仅是机构规模问题,银行系统的网络结构相对金融系统更为稳定。在外部的冲击下,金融网络结构改变,但网络自身按周期性回复结构状态。在冲击作用下网络相关性有下降,释放风险后,网络结构从线型变为中心外围式结构,但只要冲击结束,网络结构便开始恢复,金融网络是一个有弹性的网络。观察冲击规律可以发现,在发生正向冲击后,网络结构滞后一个时段出现平均偏心距上涨,网络结构变得松散,发生负向冲击时,网络结构的平均偏心距立即下降。但在冲击结束后的指数振荡期,网络结构都会对冲击的结果快速恢复。从图2可以看到系统性风险和网络结构没有趋势性关系。
我们以金融系统平均偏心距为观察点,经过采样,网络的偏心距在2015年4月16日达到最高值18.03774,在2015年9月23日达到最低值7.811321。在以上两个时间点的生成树如图3。可以看到2015年4月16日的生成树呈线形结构,而2015年9月23日成分层结构(中心-外围式结构)。在2015年4月16日,由于杠杆作用,推动了金融机构总市值的上涨,这种相关性主要是金融杠杆造成的,消弱了机构之间的产业关联性,金融系统的结构变得松散,表现为线型结构。而2015年9月23日,风险释放,相关性降低,金融系统产业关联性显现,可以清晰地看到在图3 b中,银行系统分属几组连接在一起。在冲击下,金融系统释放了风险到外部经济系统,网络结构变为分层结构(中心外围式结构)。
图4是θ=0.7时,金融网络压缩成相关性网络后的是相关性网络的平均偏心距、金融平均互信息系数、金融指数的比较。基于相关性的压缩可能会出现离散的点,离散的点表明该机构与金融系统中其它的机构没有很强的联系。
相关性网络的偏心距同时受相关性与网络结构的影响。首先,我们观测到相关性较高的时间段,平均偏心距较低。这是因为在相关性高的时间,根据我们的压缩规则,相关性网络的连通度更高,所以平均偏心距偏低;而在相关性低的时刻,平均偏心距偏高。同时我们观察到冲击对网络结构的影响,可以观测到当发生正向冲击时,平均偏心距滞后上升,当发生负向冲击时,平均偏心距立即下降,但冲击结束后,网络结构立即回调,这在各个震荡期更为明显。银行机构的相关性网络与金融机构的相关性网络尽管偏心距曲线不一致,但规律一样。在相关性网络中,也显现出通过结构变化来应对冲击的特点。
我们重点观察金融指数从6月8日开始的三次下跌,第一次6月8日至6月29日,指数从224.1885下降到182.5848;第二次为2015年7月10日至2015年7月27日,指数从200.7612点下降到170.1463点;第三次为2015年8月19日至8月25日,指数从169.0346点下降到130.6283点。三次下跌期,平均偏心距的变化为第1次从3.113208下降到2.849057,第2次为从3.754717下降到3.339623,第3次为从4.962264到4.396226。
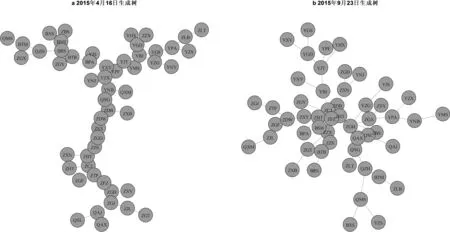
图3 不同时点的生成树
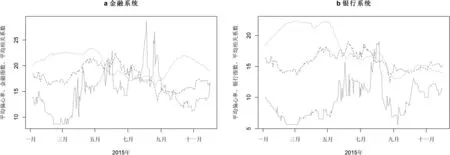
图4 相关性网络的平均相关系数、指数、平均偏心率
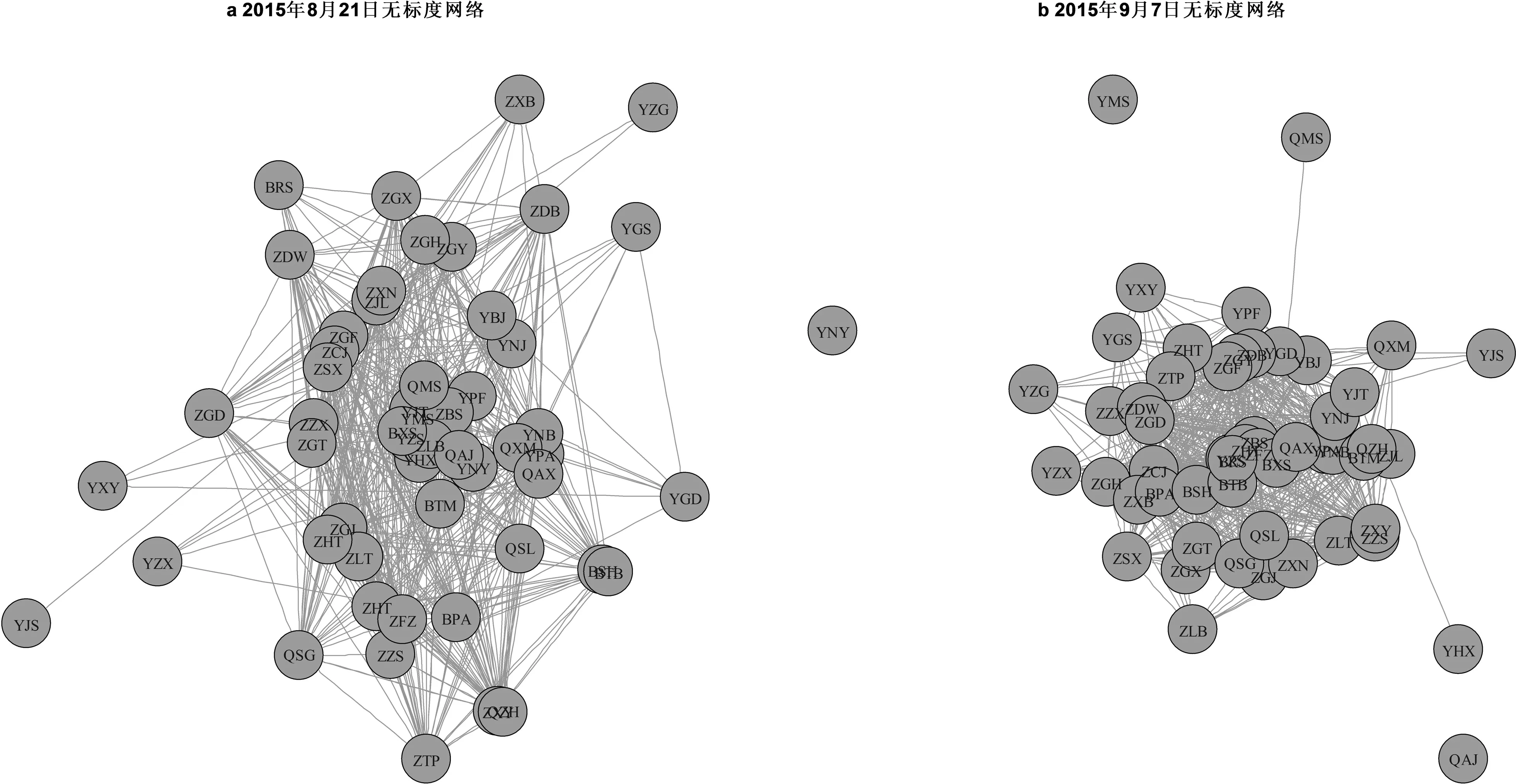
图5 不同时点的无标度网络
冲击力度一次比一次大。另外我们观察到由于相关性在降低,平均偏心距在不断上升。由于相关性,外部冲击的原因,网络结构发生剧烈的波动,适应外部变化。
我们来观察最后一次冲击后网络结构的变化。图5a是2015年8月21日金融相关性网络,图5b是2015年9月7日基本稳定后的相关性网络,平均偏心距从5.339623下降到3.056604。在此期间,平均相关系数变化不大,主要是冲击的影响。我们可以看到,在冲击前,没有离散的节点,在冲击后出现了离散的节点,证明负向冲击较大,有一些连接断裂。由于平均相关性变化不大,一些机构的连接被加强,如建设银行(YJS),在冲击前只有一条连接,在冲击后有三条连接,又如兴业银行(YXY)冲击前3条,冲击完成后10条连接。网络结构从平均偏心距的变化也可以看出,受冲击后的网络更加中心化。
网络相关性和网络结构对系统性风险都有很大的影响。从风险溢出的角度看,网络相关性的强度和网络结构对风险溢出都有显著作用。本文认为当网络结构受到冲击发生变化时,网络相关性的增强可以弥补网络结构弱化带来的风险溢出,网络相关性在实际的系统性金融风险中占主导地位。在金融系统受到冲击时,正向冲击使金融系统的网络相关性增加,系统性风险增加;负向冲击使金融系统的网络相关性减小,系统性风险减小;网络结构随着外部的冲击发生变化,但有一定的弹性。
根据上文的结论,相关性虽然与系统性风险没有单调关系,但相关性变化过程是系统性风险积累与释放的过程,而网络结构与系统性风险没有趋势关系,在冲击作用下网络结构发生震荡。本文认为对系统性风险的管理者来说,采用干预网络结构不如干预网络相关性更有效。在2015年的股市冲击下,考虑到融资融券、结构化产品、融资担保等因素,政府为了避免股市冲击导致发生系统性金融风险,对股市进行救助。为了保证救援的效果,在救市优先考虑对股指影响比较大的权重股,但效果并不明显。本文认为在下跌的间歇期,最好的救市政策是首先找到相关性变化的原因,从解决根源入手,其次是对相关性较大的机构团体救助,降低整个系统网络的相关性,利用机构间的相关性使资产的同步下跌减缓。考虑网络内部的相关性,本文使用最大团在相关性网络中挖掘全相关的机构团体。为了简单,我们选择2015年7月6日,2015年7月29日,2015年9月9日的数据来挖掘最大团。
2015年7月6日的最大团有2个,公共部分为ZTP,ZDB,ZDW,ZXN,ZJL,ZGF,ZZS,ZXY,YNJ,ZCJ,ZHT,ZHT,ZFZ。第一个团多出ZGD,第二个团多出ZZX,2015年7月29日的最大团有1个,为ZCJ,ZDB,ZHT,ZFZ,ZZX,ZXY,ZGF,ZTP,ZDW ,ZJL,ZZS,ZXN,ZHT,ZGD。2015年9月9日的最大团有两个,交集为ZZX ,ZHT, ZFZ, ZDB ,ZCJ, ZZS, ZHT,ZGX,ZGH,ZXN,ZTP,ZXY,ZDW,YPA,ZGY,ZGJ,ZGF,ZSX,其中1个中多了BSH,YNJ,ZXB,BPA,另一个为ZGD,ZLT,QSG,QZH。我们对最大团取交集,得到ZTP(太平洋),ZDB(东北证券),ZDW(东吴证券),ZXN(西南证券),ZGF(广发证券),ZZS(招商证券), ZXY(兴业证券),ZCJ(长江证券),ZHT(华泰证券),ZFZ(方正证券)等10家机构。即在市值下跌过程中,这10家机构保持很高的同步性,平均相关性明显比金融系统的平均相关性强。从原因分析,这10家机构都是证券机构,与本次系统性风险的原因主要是由融资融券的杠杆引起的有关,对这10家机构的救助,首先需要在解决融资融券杠杆问题的基础上,才能有效地防止出现系统性的风险;其次根据相关性原则,对这10家中的1家或几家机构救助,能够最大程度地改变整个金融网络的相关性,从而更有效地干预系统性风险。
五、结论与政策建议
本文建立了一个基于互信息的金融系统相关性网络,从相关性、结构两个方面研究了我国金融系统的系统性风险。在相关性方面,主要依据相关系数矩阵时间序列建立的平均互信息系数时间序列,研究发现相关性增加导致系统性风险增加,相关性对系统性风险有加强作用,但并不完全同步,在风险积聚的最后阶段,总会发生相关性分化造成平均相关性降低的现象,可以利用相关性预测系统性风险的出现。在网络结构方面,研究了最大生成树以及相关性网络的平均偏心距,发现网络结构与系统性风险没有趋势性关系。网络结构在外部的冲击下具备弹性,在受到冲击后结构更加中心化,网络结构变化是系统缓解外部冲击的一种方式。虽然静态情况下网络结构对风险溢出有显著影响,从在动态角度看,相关性与网络结构是相互影响,只有在相关性不变的情况结构比较才有意义。根据网络相关性、结构与系统性风险的关系,本文认为管理系统性风险方面,通过干预网络相关性的方式比干预网络结构的方式更有效。最后本文基于系统相关性提出了干预系统性风险的一种方法。
我国当前金融系统主要风险包括互联网金融、银行理财产品、房地产、地方融资平台等方面累积的风险,从风险溢出角度看可以分为通过银行间债务、支付渠道等引起的直接传染,以及价格、共同风险暴露引起的间接传染两类。系统性风险的主要表现一是金融空转现象,如银行系统的理财产品与投资数量之差扩大,大量资金脱实向虚,以钱炒钱,金融投机等,造成金融机构之间的关联性增加,系统性风险持续增长。二是金融经济杠杆造成机构之间相关性以杠杆倍率增加,如各种衍生品工具,融资融券带来的杠杆效应,增加了金融机构之前的关联度,累积了系统性风险;三是金融机构投资的同质化(如房地产、地方融资平台)造成的部分金融机构相关性增加,引起系统性风险增加;四是金融创新和混业经营加速,金融机构、市场、产品之间关联性加强,增加了系统性风险。为了防范和化解我国的系统性金融风险,主要的政策建议如下:
一是转变发展观念,深化金融改革。提高金融供给侧的质量与效率,实现金融去杠杆与经济稳定增长的统一,把更多金融资源配置到经济社会发展的重点领域和薄弱环节上,增强金融系统的健壮性,促进金融经济健康发展。
二是引导金融回归本源,服务好实体经济。实体经济发展是金融稳定增长的动力。提高直接融资比重,促进多层次资本市场的健康发展。发展普惠金融,在信贷方面,创新抵押物,推动信用体系建设;在债券方面,开发各种债券、证券化产品,降低中小企业的融资成本。打击非法集资、乱加杠杆、乱做表外业务、违法违规套利行为;深化利率汇率市场化改革,完善市场化利率汇率形成机制,提高服务实体经济水平。理顺金融发展与经济发展的关系,实现金融经济协调可持续发展,防止系统性金融经济危机的发生。
三是健全货币政策和宏观审慎政策双支柱调控框架。在货币政策方面运用货币政策工具与方法,保持物价稳定;在宏观审慎政策方面加强对系统性风险的监管,密切关注金融机构关联性与金融系统结构,从逆周期角度防止风险积聚,从空间维度防止风险传染,从而保持金融系统稳定。
四是健全金融监管体系。做好监管统筹与协调工作,解决监管空白与多头监管问题;强化穿透式监管,提高市场透明度;逐步适应金融机构与金融市场的创新变化,有效提高监管水平,着力防范可能出现的“黑天鹅”“灰犀牛”,着力构筑金融的安全防线,从而守住不发生系统性风险的底线。
[1]陆 婷.如何度量金融系统性风险:一个文献述评[J].金融监管研究,2017(6):1-15.
[2]Neveu A R. A survey of network-based analysis and systemic risk measurement[J]. Journal of Economic Interaction & Coordination,2016:1-41.
[3]Allen F,Gale D. Financial contagion[J]. Levines Working Paper Archive,1999,108(1):1-33.
[4] Iori G, Jafarey S, Padilla F G. Systemic risk on the interbank market[J]. Journal of Economic Behavior & Organization,2006,61(4):525-542.
[5] Stiglitz Joseph. Risk and global economic architecture: why full financial integration may be undesirable[J]. American Economic Review,2010,100(100):388-392.
[6]Gai P,Haldane A,Kapadia S. Complexity,concentration and contagion[J]. JMonet Econ . 2011,58(5):453-470.
[7]苟文均.债务杠杆与系统性风险传染机制[J].金融研究,2016(3):74-91.
[8] 唐文进.极端金融事件对系统性风险的影响分析[J].经济研究,2017(4):17-33.
[9] 郑振龙.平均相关系数与系统性风险[J].经济学(季刊),2014(4):1047-1064.
[10]Thurner S,Poledna S. DebtRank-transparency: controlling systemic risk in financial networks[J]. Scientific Reports,2013,3(5):1888.
[11]Bargigli L,di Iasio G,Infante L,Lillo F,Pierobon F. The multiplex structure of interbank networks[J].Quant Finance. 2015,15(4):673-691.
[12]Poledna S,Molina-Borboa J L,Martínez-Jaramillo S,et al. The multi-layer network nature of systemic risk and its implications for the costs of financial crises[J]. Journal of Financial Stability, 2015,20:70-81.
[13] 方 意.系统性风险的传染渠道与度量研究[J].管理世界,2016(8):32-57.
[14]Acharya,Viral V,Brownlees,Christian,Engle,Robert,et al. Measuring systemic risk[J]. Working Paper,2010,29(1002):85-119.
[15]Chen H, Cummins J D, Viswanathan K S, et al. Systemic risk and the interconnectedness between banks and insurers: an econometric analysis[J]. Journal of Risk & Insurance,2013, 81(3):623-652.
[16]Mantegna R N. Hierarchical structure in financial markets[J]. The European Physical Journal B-Condensed Matter and Complex Systems,1999,11(1):193-197.
[17]Vladimir Boginski A,Sergiy Butenko B,Panos M. Pardalosa. Statistical analysis of financial networks[J]. Computational Statistics & Data Analysis,2005(48):431-443.
[18]Brusco S. Liquidity coinsurance,moral hazard and financial contagion[J]. Department of Economics Working Papers, 2005, 62(5):2275-2302.
[19]Castiglionesi, Fabio,Navarro, Noemí. Optimal fragile financial networks[J]. Social Science Electronic Publishing,2007(100):1-39.
[20]Lenzu S,Tedeschi G. Systemic risk on different interbank network topologies[J]. Physica A Statistical Mechanics & Its Applications,2012,391(18):4331-4341.
[21]隋 聪.基于网络视角的银行业系统性风险度量方法[J].中国管理科学,2016(5):54-64.
[22]隋 聪.网络结构与银行系统性风险[J].管理科学学报,2014(4):57-70.
[23]邓 超.基于多主体建模分析的银行间网络系统性风险研究[J].中国管理科学,2016(1):67-75.
[24] Kritzman,Mark,Li,Yuanzhen,Page,Sebastien et al. Principal components as a measure of systemic risk[J]. Social Science Electronic Publishing,2010,37(4):112-126.
[25] Kolanovic M,Silvestrini D,Lee T. S. K.,Naito M. Rise of cross-asset correlations.JP Morgan Global Equity Derivatives & Delta One Strategy[EB].May. 2011,URL:www.cboe.com/ Institutional/JPMCrossAssetCorrelations.pdf.
[26] Engle R,Kelly B. Dynamic equicorrelation[J]. Journal of Business & Economic Statistics, 2012, 30(2):212-228.
[27] Rothman P. Nonlinear time series analysis of economic and financial data[M]. Springer. 1999,Vol.1.
[28] Dionisio A,Rui M,Mendes D A. Mutual information: a measure of dependency for nonlinear time series[J]. Physica A Statistical Mechanics & Its Applications,2004,344(1-2):326-329.
[29] Darbellay,Georges A. An adaptive histogram estimator for the mutual information[R]. 1996.
[30] Jain N,Murthy C A. A new estimate of mutual information based measure of dependence between two variables: properties and fast implementation[J]. International Journal of Machine Learning & Cybernetics,2016,7(5):857-875.
[31] Artzner P,Delbaen F, Eber J, Heath D. Coherent measures of risk[J]. Mathematical Finance,1999,9(3),203-228.
