活动探究构模型，符号诠释透思想

陆 兵

[摘  要] 教学“平方差公式”时，应高度重视方案设计，引导学生正确认识公式，并掌握公式. 同时，应在教学中渗透数学思想方法，提升学生的思维能力. 本文从活动设计、探究过程、公式符号和思想渗透四个层面思考其教学.

[关键词] 乘法公式;活动;模型;思想;符号

乘法公式是在多项式乘法基础上，由一般到特殊总结出的公式，其作为苏科版七年级下册的重要内容，教学中需要学生不仅掌握公式的具体内容，还要掌握公式的推导过程，并能灵活运用公式解决问题. 这就需要教师充分研读教材，合理处理教学难点，制定科学的教学方案. 下面以第2课时的“平方差公式”为例，展开教学思考.

关注教学的活动设计

“平方差公式”作为重要的乘法公式之一，教学的关键在于如何使学生充分参与教学，并充分探究公式，逐步理解公式. 如果采用传统的记忆训练教学模式，它虽然也可以使学生掌握公式，但显然学生的积极性不会高，教学效果也不会好，难以形成互动的教学氛围. 考虑到平方差公式是一类规律性公式，且知识源于具体的情境，因此，教学“平方差公式”时可以采用活动探究的方式——引导学生发现规律，提出猜想，证明公式，形成认识.

采用活动探究的方式教学“平方差公式”时，需要合理地编排教学环节，设计丰富的教学素材，提升学生参与度的同时引导学生主动思考. 可以按照如下流程来实施教学：情境引入，问题给出→活动探究，构建模型→自主认识，形成公式→合作讨论，强化理解. 在第一环节的引入阶段，可以设计具体的问题情境，也可以结合富有历史文化感的问题，从问题中引出公式左边相乘的形式，引导学生发现其中的数式规律，激发学生思考. 接着，在第二环节设计图形面积探究活动，借助图形的直观性来呈现公式的证明过程，使学生从“数”与“形”的角度完成公式的辨析. 而在探究的第三环节，则需要引导学生自主思考，总结平方差公式的结构特点和表示方法，完成理解性记忆. 在最后的强化阶段，则十分有必要设计一些公式变形类试题，让学生在讨论中完成解答，从中积累经验，完成对公式的强化运用.

重视模型的构建过程

平方差公式是在多项式乘法基础上总结出的规律性公式，虽然属于单纯的代数公式，但如果仅采用代数变换的方式来完成教学证明，学生仍然难以理解. 考虑到学生的认知能力，结合数式的证明方式，可从数形结合角度来完成公式的证明，即构建直观的模型，从模型中衍生出公式，从而证明公式.

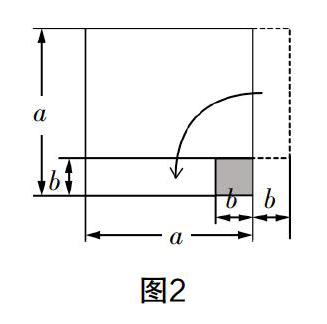
平方差公式的证明可以借助几何的面积模型，通过求解面积的不同方式来完成. 教学中可以从现实的问题中抽象出模型，如给出问题：已知边长为a的正方形绿化坪，由于道路设计要求，需要将它的一边减小b米（b<a），另一边增加b米，试分析绿化坪变化后的面积. 此时需要引导学生构建面积模型，如图1所示，其中①为变化前的正方形——边长为a，而变化后的图形为长方形，相邻两边的长分别为a+b和a-b，如图1中的②. 学生很容易利用长方形的面积公式得出变化后的绿化坪面积为（a+b）（a-b），此时需要进一步让学生分析两个图形之间的面积差异，即在同一个图形中表示出图形的变化，如图2. 学生很容易发现，如果将长方形右侧部分移到图形的下方，则图形由正方形变为长方形后，面积减少了右下角一个边长为b的小正方形，即变化后的图形面积为a2-b2. 结合长方形面积的唯一性可得（a+b）（a-b）=a²-b²，于是我们利用图形完成了平方差公式的几何证明.

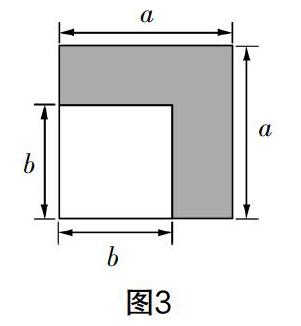
在构建证明模型阶段，也可以进一步采用剪纸的方式，引导学生通过动手操作，亲身体验证明过程. 可让学生准备一张边长为a的正方形纸片，然后按照图3所示的方法剪去一个边长为b的小正方形（b<a），让学生思考如何计算剪去后剩余部分的面积，引导学生采用拼接的方式（如图4）将剩余部分拼成新的长方形，分析其相邻两边的长度，从而获得面积关系. 学生根据图3的剪纸过程很容易得出剪去后剩余部分图形的面积为a2-b2，而对于图4，首先应引导学生分析两个梯形的底和高，即底分别为a和b，高为a-b，然后分析组合为长方形后长方形的长和宽，即长为a+b，宽为a-b，再利用面积公式得出拼成的长方形的面积为（a+b）（a-b）. 在此基础上，引导学生分析图形之间的面积关系，从而得出（a+b）（a-b）=a²-b²，完成对公式的证明. 学生在动手操作的过程中更能产生深刻的认识，更能理解公式.

强化学生的符号意识

教学“平方差公式”时，较为重要的一个环节是使学生充分认识公式的结构特点，学会用数学语言描述公式，摆脱机械的模仿. 该环节除了使学生掌握公式外，还兼具强化学生符号意识的目的，且后者才是公式规律总结的意义所在.

进行公式的规律总结时，可以采用多种方式，可先引导学生利用平方差公式的内容完成图5问题的填空——图中将平方差公式左侧部分用具体的文字、图形和字母进行替换，学生在分析过程中很容易得出两数之差和两数之和相乘的公式特征. 然后，在第二环节给出具体的平方差公式——（a+b）（a-b）=a²-b²，引导学生分析公式中字母a和b所表示的具体含义，得出a表示符号相同的整式，b表示符号相反的整式，从而使学生理解公式内容的广泛意义. 而在最后阶段，则需要学生在充分认识公式结构特征的基础上，用文字语言和符号语言来进行概括，充分理解公式的本质属性，从“代数和”与“代数差”的角度完成对公式的认识.

利用数学语言和文字语言对平方差公式的结构特征进行总结和规律概括，是帮助学生认识公式、灵活运用公式的重要手段，尤其在后续解决一些平方差变式问题时，需要学生利用对公式的特征理解来完成变通求解，而不拘泥于公式的固定形式. 同时，在对公式进行语言描述的过程中，可以培养学生条理表达的能力，提升其数学素养.

注重思想方法的渗透

平方差公式以及后续的完全平方公式等乘法公式，均是在多项式乘法运算基础上进行的知识总结，而对于公式的总结过程和证明过程，其背后均蕴含着丰富的思想方法，即公式的形成是在数学思想的指导下完成的，因此在教学中十分有必要结合具体的内容完成数学思想的本质揭露.

平方差公式的形成背后蕴含着数学从一般到特殊的思想，因此在教学的初始阶段以及最终的应用阶段，有必要给出一系列的平方差问题，使学生从一般的数式运算中总结特殊的规律，并利用特殊的规律完成一般问题的求解，实现规律的总结与应用，并获得规律形成的思想认识.

而在公式的概括和证明阶段则蕴含着数学的模型思想、数形结合思想和抽象思想. 根据具体的问题构建数学模型，是模型思想的应用体现;而利用几何模型抽象数学公式，完成公式的概括，则渗透着数学的抽象思想;整个图形的证明过程则是数形结合思想的应用. 考虑到学生的认知能力相对较弱，缺乏相应的思想基础，教学中，我们不能将数学思想剥离开来，也不能直接忽视，以免造成数学思想的缺失. 我们应结合教学内容，设置具体的教学环节，使学生充分体验利用数学思想方法完成知识探究的具体过程，并在探究过程中逐步积累应用思想方法的技巧. 如在从一般到特殊思想的滲透阶段，呈现多样的平方差公式问题时，有必要提醒学生与其他多项式的乘法形式相比较，从而认识其特殊性;而在数形结合思想的渗透阶段，可以引导学生掌握该思想的一般思路：分析题干→提炼数据→绘制模型→分析模型→构建数式关系.

数学教学因思想而深刻. 在思想方法的指引下完成对公式的探究，更能强化学生对公式的认识，其对学生感悟思想、提升数学思维有极为重要的推动作用，且对学生的后续发展意义重大.

总之，“平方差公式”作为通过多项式乘法总结出的规律性公式，其探究过程及教学方式具有一定的代表性，教学中可采用活动探究的方式，利用模型完成公式的证明，引导学生关注公式的符号语言，渗透数学思想方法，通过合理的教学设计使学生在掌握知识的同时接受数学思想的熏陶.