浅述费马引理和罗尔定理

文/佛山市顺德区第一中学 魏竞彤

一、引言

高中数学里面在讲到函数y＝f(x)的单调性、极值问题时，常用到导数，求出导数为零的点，即：f′(x)＝0时，x的取值。我们知道假设这个取值为x＝x0时，那么，如果在 x0附近的左侧 f ′(x)＞0，右侧 f ′(x)＜0，那么f(x0)是极大值。如果在 x0附近的左侧 f ′(x)＜0，右侧 f ′(x)＞0，那么 f(x0) 是极小值。

二、由极值点到费马引理

在费马引理中：函数f(x)在点ξ的某个邻域内有定义，并且在ξ处可导，如果对于任意的x∈U（ξ)， 都 有 f(x)≤f(ξ)(或 f(x)≥f(ξ))，那么 f′（ξ）＝0。

也就是：函数在某点周围的附近内有定义，而且在这点导数存在，那么在这个点周围附近处，如果任何数的函数值比这个点的函数值都大或者都小，那么这个点的导数为零。为什么呢？

假如这个点周围附近的点的函数值都比这个点的函数值大或者小，这个周围它不是一个方向，它是n多个方向，那么这个点就是最值点，而我们知道最值点也就是极值点，除非它是无定义点，那我们条件中已表明它是有定义的，所以这个点是极值点，即这个点的这个函数的导数在这一点为零也就是费马引理中的 f′（ξ）＝0。

三、由函数单调性以及极值点到罗尔定理

在罗尔定理中：如果函数f(x)满足以下条件:

（1）在闭区间 [a，b]上连续，

（2）在开区间 (a，b)内可导，

（3）在区间端点处的函数值相等，即f(a)＝f(b)，则至少存在一个 ξ∈(a，b)， 使得 f′(ξ)＝0。

这个定理叫做罗尔定理。

函数在闭区间 [a，b]上是连续的，且在 (a，b)内可导，且满足f(a)＝f(b)，那么我们分情况讨论：

这种情况下：函数在闭区间[a，b]上是连续的，且在开区间 (a，b)内可导，f(a)＝f(b)，显然它是存在极值点的，因为C、D俩点就是函数的极值点， f′(xc)＝f′(xD)＝0， 所以 C、D就是那个存在的 ξ∈(a，b)，使得 f′(ξ)＝0。

这种情况下:函数在任意闭区间上都是连续的，且在任意开区间内可导，f(a)＝f(-a)，显然它是存在极值点的，因为原点就是函数的极值点，所以 f′(0)＝0，所以原点就是那个存在的 ξ∈(-a，a)， 使得 f′(ξ)＝0。

这种情况下：函数在任意区间是连续的，在任意区间也可导，也存f(a)＝f(b)，但是它是一个常函数，任意点的的导数都为零，所以任意点都是那个存在的ξ∈(a，b)，使得f′(ξ)＝0。

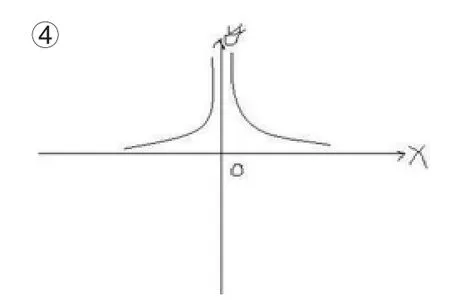
这种情况下：函数在原点不是连续的，在原点也不可导，那么它的极值点在原点无法讨论。那么我们把它分成俩只曲线：对于左边（-∞， 0）讨论， 不存在 f(a)＝f(b)， 所以不满足罗尔定理的条件。同理可得，右边 （0，+∞），也不存在f(a)＝f(b)，所以也不满足罗尔定理的条件。我们可以从图像中看出，除了0点，没有极值点，但是0点不可导，所以不存在任何一点ξ，使得f′(ξ)＝0。

这种情况下：函数在任意区间是连续的，在任意区间也可导，但是不存在f(a)＝f(b)，所以不满足罗尔定理的条件。这是一次函数，我们可以知道，一次好书的导数为一个非零常数，它没有极值点，所以在任何一点，它的导数都不为零，所以也就不存在任何一点ξ，使得f′(ξ)＝0。

其实我们可以从罗尔定理的条件出发，一个函数若满足f(a)＝f(b)，且闭区间 [a，b]上是连续的，在开区间 (a，b)内可导，那么这个函数只有俩种情况：一种是有起伏的，存在单调递增，单调递减，且函数在这个递增递减变化的区间内连续且可导，那么这个变化的瞬间也就是极值点，这一点导数为零，也就是 f′(ξ)＝0。 也就是说它是符合罗尔定理的，那么这个ξ有多少个呢？没有确定值，根据函数不同，ξ的个数也不同。还有一种情况是没有起伏，也就是任何点的函数值都相等，也就是所谓的常函数了，如上第三种情况，它也是符合罗尔定理的。

四、 由费马引理到罗尔定理

在第三点由函数单调性以及极值点到罗尔定理中，我们对罗尔定理的推导是依靠函数图像来推导的，有一定的不严谨性，那我们以更加严谨的方法来推导，我们从费马引理来推导罗尔定理。

证：由于 f(x)在闭区间 [a，b]上连续，而闭区间内，连续函数一定有最大值和最小值定理 （不管是函数值变化的函数还是函数值不变的函数，都有最大值和最小值。注：常函数最大值最小值就是这个常数）。也就是说f(x)在闭区同 [a，b]上必定取得它的最大值M和最小值m，这样，只有两种可能情形:

（1） M＝m。 这时 f(x)在区间[a，b] 上必然取相同的数值 M＝f(x)＝m。 由此， ∀x∈(a，b)， 有 f′(ξ)＝0。因此， 任取 ξ∈(a，b)， 都有 f ′(ξ)＝0。这种情况即为常函数图像，如下图：

(2)M＞m， 因为 f(a)＝f(b)， 所以M和m这两个数中至少有一个不等于f(x)在区间 [a，b]端点处的函数值，为确定起见，不妨设M≠f(a)≠f(b)， 那么必定在开区间 (a，b)内有一点 ξ， 使 f(ξ)＝M， 因此， ∀x∈[a，b]， 有 f(x)≤f(ξ)， 满 足 费 马 引 理的条件，从而由费马引理可知f′(ξ)＝0。 假如 m≠f(a)≠f(b)， 那么必定在开区间 (a，b)内有一点 ξ，使 f(ξ)＝m， 因此，∀x∈[a，b]， f(x)≥f(ξ)，满足费马引理的条件，从而由费马引理可知 f ′(ξ)＝0。 例如； 下图图中，在图像所示区间内M＝4，m＝-4； 存在点 ξ1， 使 f(ξ1)＝m＝-4≤f(x)，存在点 ξ2， 使 f(ξ2)＝M＝4≥f(x)， 那么 f′(ξ1)＝f′(ξ2)＝0。

所以，我们可以推导：如果函数f(x)在闭区间 [a，b]上连续，在开区间 (a，b)内可导，且在区间端点处的函数值相等，即f(a)＝f(b)，则至少存在一个 ξ∈(a，b)， 使得 f′(ξ)＝0。