结构阻尼比的识别

（黄冈职业技术学院建筑学院， 湖北 黄冈 438002）

0 引言

在动荷载作用下，结构发生振动，在这个过程中，如果停止对结构输入外部的能量，则结构的振动随之会逐渐减小直至静止。整个过程中，使结构所具有的能量逐渐减小的因素称为阻尼。对于工程结构而言，阻尼产生的原因是指如何将结构的振动能量变成可以耗损的能量，进而减弱结构的振动、噪声以及冲击。在结构振动的动力特性分析中，由于阻尼都直接或间接影响着各种响应，因此，如果想提高结构动力响应分析的可靠度，其中一项重要的任务就是要相应提高结构阻尼比估计的准确度。

1 阻尼比识别方法

1.1 共振放大法

当受到简谐荷载作用时，具有粘滞阻尼的单自由度体系将产生振动，其响应包括两个不同的振动成分：瞬态振动和稳态振动。通常，振动中的瞬态部分在体系阻尼的影响下会很快衰减掉，因此，振动一段时间后会发现，单自由度体系的振动仅剩稳态部分。此时，体系的振动响应可以表示为：

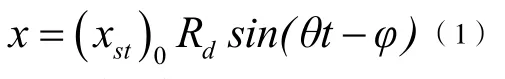
式中，(xst)0是体系最大静位移，Rd是动力放大系数，它的表达式如下：

若简谐荷载的频率很接近或者等于体系的固有频率，则体系将出现共振现象。因此，如果能得到动力放大系数的变化曲线，就可以识别出体系的阻尼比。由于动力放大系数的曲线很难确定，所以，通常情况下用一个频带（包含固有频率）的简谐荷载激励体系，测得多个x0，取其中的最大值

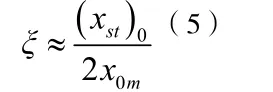
由于实际工程建筑结构的阻尼比都很小，因此，采用这种近似代替的方式，对阻尼比的识别所产生的误差也比较小。

综上所述，用上述方法识别体系的阻尼比，理论上是十分简单的。但是，实际操作时却是困难重重。其中，静位移的实际测量无论是在加载设备方面还是在记录设备方面都很难实现。因此，在工程结构的阻尼比实测中，该方法并没有广泛地用于识别建筑结构的阻尼比。

1.2 半功率带宽法

若按时域法和频域法进行分类，则半功率带宽法是一种通过频域的方式进行阻尼识别的。频响函数具有很重要的作用，它使得系统的位移响应与系统的外部激励在频域内联系了起来。单自由度体系的位移频响函数表达式如下所示：

令而且对于实际建筑结构，其阻尼比通常都很小，而当阻尼比很小时有：

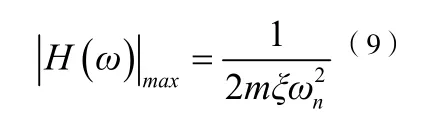
综上所述，在系统的幅频曲线上画一条水平线即可利用式（13）计算阻尼比。显然，利用半功率带宽法避免了求静位移所遇到了难题，但是也存在误差，产生误差的主要原因有即式（13）中的固有频率及半功率带宽对应的频率的确定。

1.3 自由衰减法

通常情况下，自由衰减法主要用来对单自由度体系的阻尼比进行识别。在一定的初始条件下，单自由度体系将发生自由振动，其位移响应的数学表达式如下：

式中体系的有阻尼振动频率的表达式如下：

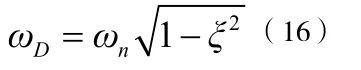
若在t=ti时的质点响应为一个峰值点xi，并且在时响应

为相邻峰值点xi+1。任意两个相邻振动峰值之比为：

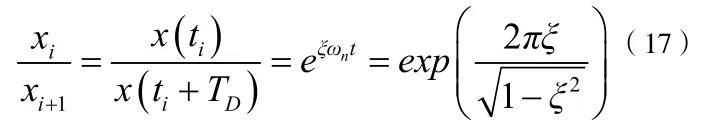
其中，TD是体系有阻尼振动的周期。由此可见，任意两个振动峰值之比与起始时刻ti无关，仅与阻尼比ξ有关。定义δ等于体系振动响应的相邻周期的峰值的比值的自然对数，也叫对数衰减率，它的计算公式如下：

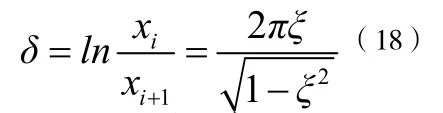
事实上，就生活中的工程结构来说，它们的阻尼比普遍都很小，故而，通常情况下故实际建筑结构的阻尼比近似的表达式如下：

当建筑结构的阻尼比很小时，其自由振动的衰减会很缓慢，此时，为了提高阻尼比识别的精度，可以取间隔好几个周期的峰值来计算，可得：

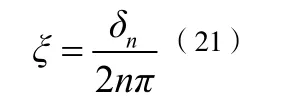
由于对于单自由度体系而言，自由衰减响应只包括了一阶模态，而就多自由度体系而言，它的衰减响应不仅有一阶模态的成分，还包括了很多高阶模态响应，因此式（21）仅使用于单自由度体系。而实际结构基本上都是多自由体系，若想用自由衰减法识别多自由度体系的阻尼，应该对采集到的多自由度体系自由衰减响应进行频谱分析，根据所需的模态阶次选取一个频带。然后，对实测自由衰减响应进行带通滤波，这样得到的就是所需阶次的单独的模态响应，此时便可通过式（21）进行阻尼比识别了。这个方法是将多自由度体系的响应进行分解，从而得到很多单个的等效的单自由度体系，这些体系是以相应阶数的模态频率作为其固有频率的，之后再利用自由衰减法识别各个体系阻尼比。。

2 结论

目前，阻尼比的识别方法多种多样，它们基本上属于时域识别法或者频域识别法这两种类型，比较常见的如：共振放大法、半功率带宽法、自衰减法、Hilbert包络法、随机减量法、小波变换法、HHT 法等等。在一定条件下，这些方法都能够识别出阻尼，只是识别的难易程度与识别精度不一。本文主要介绍共振放大法、半功率带宽法、自由衰减法这三种识别方法。这三种阻尼识别方法是最基本的，不但识别精度较高，理论成熟，而且适用范围也较广。其中，利用自由衰减法来识别结构的阻尼比最为常见。

[1]吴启昌．材料及结构件阻尼特性的测量及应用研究[D]．哈尔滨：哈尔滨工业大学，2010．

[2]胡哲，宋显辉等．振动法测量材料弹性模量与阻尼比[J]．固体力学学报, 2008, 29：155-157．

[3]樊海涛．钢筋混凝土建筑非线性阻尼性能及其地震反应研究[D]．湖南：湖南大学， 2005．

[4]宫建平．阻尼系数的测定[J]．晋中学院学报，2011，28(3)：1-3．