高渗透率分布式电源并网的无功电压控制研究
2018-03-02胡力中詹跃东程军照陈先富张少泉吴明伟
胡力中+詹跃东+程军照+陈先富+张少泉+吴明伟

摘要:为了解决当不同情况下高渗透率分布式电源并入电网时,在传统配电和输电系统中出现一些电压波动较大、网损过高等问题。本文提出一种改进型自适应遗传算法应用在无功电压控制中。首先,采用线性标定的方法对5个最小化问题的目标函数进行标定,加快算法在后期的收敛进程。其次,并采用NSGA-Ⅱ快速非劣支配排序法来求取其中的Pareto前沿解,则多目标问题可化为单目标优化问题。最终可以减少迭代次数,具有很好的全局寻优能力和较快的后期收敛速度,可以使得把最小网损和电压偏差作为目标函数的解多样化且最优。这样高渗透率分布式电源并网条件下的系统电压更稳定,网损减少,从而增强电力系统电能质量可靠性。本文采用把输配电电系统相结合的改进型IEEE30节点模型作为研究对象,探究了输配电系统在含不同渗透率分布式电源下的几个重要指标,其仿真结果证明了本文方法的可行性和有效性。
关键词:分布式电源;无功电压控制;改进型自适应遗传算法;输配电系统
0 引言
分布式电源( DG)世界各地已经推广应用,尤其是光伏发电行业在我国已经发展为世界首屈一指的太阳能应用市场。这得益于国家颁布相关政策鼓励支持安装分布式电源的政策。分布式电源指的是可以包含任何安装在用户附近的发电设施。文献指出分布式发电是满足终端用户需求、接在用户侧附近的小型发电系统。因此,分布式发电已成为新世纪智能电网的重要发展趋势,它以高供电质量、高可靠性的效益和友好的环境得以快速发展。但随着高渗透率的分布式能源接入配电系统中,接入技术要求未来主动配电系统具有新的灵活的可重构拓扑、新的继电保护、新的检测方案、新的电压控制。虽然分布式发电技术有着环保等众多优点,但其自身不稳性却为新能源的发展带来不小的问题。其中文献中提出DG为不可控电源,大规模的并网会影响潮流分布和潮流方向的变化以及对电压的冲击,进而影响到网损的变化,最终给电网和用户带来很多不必要的麻烦。随着大量分布式电源的并网,对于现阶段的配电和输电网,还有很多地方需要改善提高。目前的配供电系统仍然是处理一些低渗透率的分布式发电,实际上其很多问题和对接入的影响还是未知的、不明确的,需要我们做进一步的研究。
高渗透率的DG并网会使输配电网的无功电压控制难度加大,系统的可控性随之降低等问题。针对上述含高渗透率DG的无功优化问题已有大量文献做了相关研究,如文献提出的直接加权求和法,但在求解多目标函数解时其不同的量纲使得权重系数难以决策并且难以解决非凸空间的寻优问题不能体现优化结果多样性。文献提出的基于模糊理论的隶属度法,它能克服直接加权求和法中加权系数不易确定的问题,但需要求解每个目标函数的隶属度其计算时间随目标函数数量的增加而变长。文献中提出一种改进入侵杂草算法,和传统的相比其易陷入局部最优和收敛精度不高等缺陷得到一定改善。但未加入DG出力不确定性因素,所得优化结果不能真实反映配电系统实际运行情况。文献提出的遗传算法对含DG的配电网进行无功优化,对求解非线性多目标的函和减小网损有一定效果。但其中的迭代次数多时间久,伴随复杂的译码,易早熟且后期收敛速度慢等缺陷的处理不是很理想。文献提出的粒子群优化算法,与上诉遗传算法相比规则更简单,搜索速度更快,但此法具有一定的不稳定性,参数不易决策,搜索精度不高且容易陷入局部最优等问题。
基于此本文提出一种探索式的方法一改进型白适应遗传算法(Modified Self-adaptive GeneticAlgorithm,MSGA)去解决网损、电压偏差以及电能的有效传输问题。因为,它是一种目前在电力系统中被工程师广泛应用于无功电压优化控制的控制方法(VQC)。本文应用一种改进型的白适应遗传算法进行一些观测性试验,以探究当高渗透率的DG引入系统时的无功电压控制问题。它通过线性标定法和NSGA-Ⅱ快速非劣支配排序法的结合可以减少迭代次数以及缩短迭代时间,具有很好的全局寻优能力和较快的后期收敛速度。本试验的实施是基于改进型的IEEE30节点模型,对含不同渗透率比例分布式电源下的输配电节点电压、网损、机端输出无功等重要指标做了一定探究,仿真结果显示在引入改进型的自适应遗传算法后上述各指标的越限点都得以约束在可控范围之内。
1 限制条件和控制变量
1.1 控制变量的约束限制
在电力系统中的无功电压控制变量包括同步电容器组输入量,可控有载变压器档位,和机端电压。本文中的控制变量定义为向量X,如下:
式中,Ca-a点的同步电容器输入量;LTb-b点的有载变压器档位;Vg,c-c点的机端电压值;K-同步电容器投入组数;L-可控有载变压器个数;M-发电机数量,其中:
Cmin≤ C≤ Cmax
(2)
LTmin≤ LT / LTmax
(3)
Vg, min≤ Vg≤ Vg, ma
(4)
运行系统的约束条件被分为两个部分,两部份约束条件分别是节点电压和发电机端无功功率。
Vn,min≤ V≤ Vn,max
(5)
Qg,min≤ Qg≤ Qg, max
(6)
其中,Vn ,nin,Vn,max-节点电压的最低和最高值。
Qg,min,Qg,max-发电机端无功电压的最低和最高值。
这样设置的原由是为了确保系统中每个节点的电压以及电机和同步电容补偿器所产生的无功功率不会超过允许的可控范围。
1.2 目标函数和适应度函数
此函数的目的使在系统中得到功率损失的最小值,降低电压偏差,保持电力系统稳定性。 式中,J-目标函数;,一适应度函数;N-节点数;M-电机数;W1,W2-權重因数;△Vn-节点电压偏差;△Qm-电机无功功率偏差;Ploss一总的输电损耗。endprint
2 改进型自适应遗传算法
遗传被分为了五个部分,每个部分功能依次为产生原始种群(即初始化)、选择运算、增殖运算、杂交运算、突变运算以及评估判断。它是一种通过模拟自然进化过程搜索最优解的方法,它是一种智能随机搜索方法的推广。对于目标函数中最优解的产生和问题的搜索扮演者不可或缺的重要角色。遗传算法不能直接处理问题空间的参数,必须把它们转换成遗传空间的由基因按一定字符编码结构组成的染色体或个体。
首先我们设定原始种群为NPo,DG的种类、有功的输出量、无功功率为染色体并采取实数矩阵编码。例如对于8节点系统而言,可以营建表l所示的染色体:
交叉运算和变异运算组成了遗传运算,其中,交叉运算用双切点交叉而变异运算用对无功功率与有功功率的扰动来实施。其中,变异概率表征一定的广域搜索能力,在算法运行中,可通过迭代次数或者所得的解来减小变异概率,从而加快算法的收敛,达到白适应的目的。遗传算法须要从给定的种群中遗传出NPO个新种群。为了求取适值函数,需要对目标函数进行适值标定,使之成为遗传算法可用的适值函数。本文采用线性标定的方法对5个最小化问题的目标函数进行标定,即:
F=Jmax-J+ξk
(9)
式中:Jmax一目标函数的最大值;J-目标函数;ξk一一个较小值;k-迭代次数
这样设定是为了加快算法在后期的收敛进程。另外,也是为了达到在随着迭代次数的增加其种群多样性增多但数量却在减少的目的。这样可以减少迭代次数,压缩运行时间,从而达到优化整个运算系统的目的。
本文算法中的选取策略的核心是求出Pareto最优解。设第i代种群中有NPi个染色体,并采用NSGA-Ⅱ快速非劣支配排序法来求取其中的Pareto最优解。其中选择方法采用变加权系数法,先对各个目标适值函数Fi进行归一化处理,设Fi的权系数为ωi,则多目标问题可化为单目标优化问题,即:
其中,ωi是0-l的隨机数。
这样能够达到优化解的目的,整个遗传算法流程图如图l所示:
3 算例分析
图2为被划分为输电系统和配电系统的模型图。整个系统包括30个节点,41条支路,2个发电机,4个同步电容器,2个双绕组变压器,2个三绕组变压器以及系统中的负载总量为284.3MW。对于我们整个研究而言需设定以下几个量,首先把分布式电源渗透率为0%的配电网作为研究的基准线,每次计算要进行5次。在配网侧以每隔10个单位容量增长的形式引入渗透率为10%-50%的分布式电源。另外,保持分布式电源接入配电网的渗透率为50%的同时,另外在输电网侧分别引入容量等同于总负荷的25%和30%的负载。
3.1 输配电系统节点电压分布
基于仿真结果如图3(a)所示,当配网各节点的DG渗透率为20%时,节点11的电压超过了正常运作范围(0.9~1.1[pu])。当DG的渗透率为45%时,节点13的电压同样超出运行范围。当配电网中DG渗透率达到50%,同时我们分别在输电网中节点7和8处并人容量为总系统负荷12.5%的负载(共25%),此时我们可以观察到节点12的电压已经超出了运行电压范围。在配电网侧条件不变情况下,把输电网侧并入的负载量提高到30%,则可由图3(b)看出节点9处电压开始就超出可控范围,这样就会引起系统电压的不平衡,如果没有DG引入系统,系统中每个节点的端电压在正常运行电压范围内会更加的可靠稳定。
当引入了遗传算法后其仿真结果变得多样是因为SGA是一种对最优解随机搜索的过程。对于DG渗透率每增长10%的过程要进行5次计算,取其平均值作为适应度值才是合理的。随着大量DG并网量的增加其适应度值也随之上升。由方程式(7)和(8)可得,当适应度值上升时,系统功率损耗反之会降低。根据图4(a),在系统中应用了MSGA后,配电网中各节点电压的分布情况得以改善和控制,它们基本上都保持在正常电压运行范围内的水平。同理,如图4(b)所示,在系统中应用了MSGA后,其输电网系统中所有节点的电压都保持在正常电压运行范围内。
3.2 输配电系统总功率损失
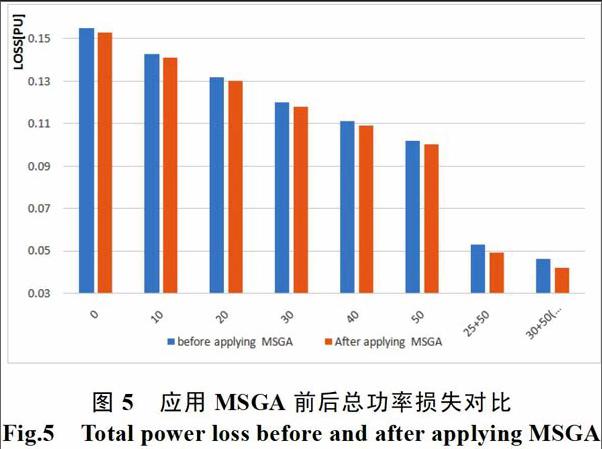
在每种条件下的总功率损失如图5所示。由于大量DG的并网后,系统总功率损失相应随之减少,由此说明DG对一些负荷节点处的有功功率有一定支撑作用,因此从电机流向负荷节点的功率有较小的损失。另外,从一条母线到另一条母线的潮流出现的功率不足会得到一定的改善,通过应用SGA来协调控制无功功率,在长距离母线中传输出现的无功功率不足等问题将会得到较好的处理。所以,在控制算法中启用SGA后的系统功率损失会小于启用之前的。
3.3 发电机端无功功率
通过协调控制同步电容器补偿电机中所消耗的无功功率并使系统中功率损耗降到最低。在系统中,通过一些设定在约束条件下的设备来产生和吸收无功功率,大多数是由发电机产生的无功功率。同时,随着DG并网数量的增加其无功功率也随之增加。
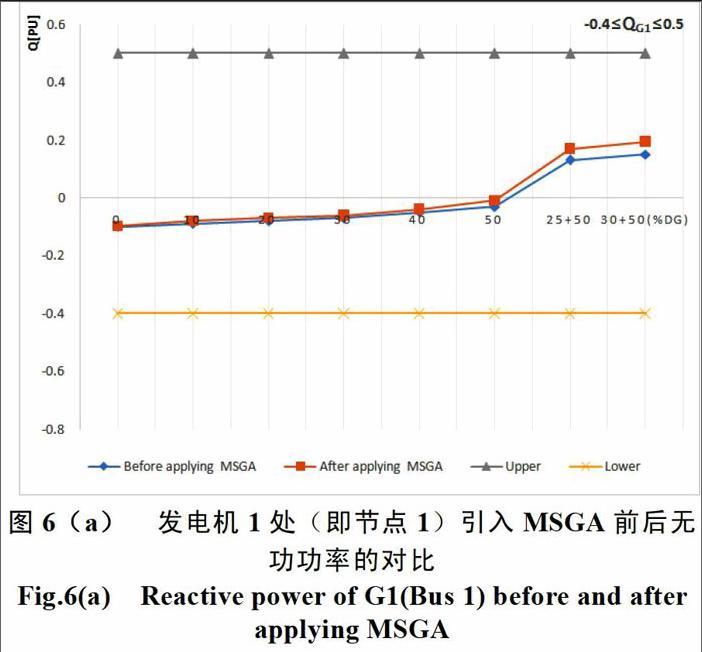
如图6(a)所示,随着DG并人数量的增加发电机1处的无功功率也随之增加但仍然保持在无功限制范围内(-0.4≤QG1≤-0.5)。应用MSGA前后对比差距不大,图中横坐标在50%以前的部分基本没有差别,其后半部分在应用了MSGA后其无功功率得到了一定的提升,效果相对比较显著,这样使系统的稳定性得到了一定的改善。
如图6(b)所示,对于发电机2(PV-节点)处的无功功率而言,系统中随着DG并网数量的增加其无功功率相应的随之降低。当达到在配电网侧以50%的DG渗透率并入,同时在输电网侧引入容量为总负荷的25%和30%的负载时,其无功功率会继续下降且已经超过了无功功率规定限制条件下的范围(-0.4≤QG1≤-0.5)。当在控制算法系统中应用了MSGA后,发电机2处的无功功率有了明显的提升,并且在图中横坐标为50%的后半部分,其无功功率已经控制在限制条件范围之内,相应的改善了整个系统的稳定性。
4 结论
本文在无功电压控制中引入白适应遗传算法后,对高渗透率DG并网条件下系统电压冲击大、网损高等问题做了仔细的探究。其中每个节点的电压会相应的随着DG并网数量增加而增加乃至越限,由于系统中DG渗透率的增加其无功功率会随之降低。在无功电压控制中应用改进型遗传算法的目地是为了把输配电系统中的节点电压分布和发电机输出无功功率保持在满足约束条件下的可取的范围之内。仿真实验表明,在含不同渗透率DG的输配电网中各节点电压、发电机处输出无功功率均保持在可控裕度范围内并且优化了总网损量。验证了引入的白适应遗传算法的可行性和有效性,从而改善了电力系统的运作效率以及各项性能。endprint