泊松公式及其应用
2018-03-02杨帆
杨帆
(盐城工学院电气学院,江苏 盐城 224053)
在理论力学教程中,研究转动参照系时介绍并运用泊松公式。文献也讨论了泊松公式及其应用。朱建阳认为,在理论力学教程中“如能适当提前介绍转动参照系的初步知识,从而引出泊松公式,则速度、加速度在极坐标、柱坐标、自然坐标、球坐标等曲线坐标中的正交分量就能顺利解决。”本文利用单位矢量的模恒为1,计算单位矢量对时间的导数,运用两矢量的标量积、矢量积公式推导出泊松公式,并系统讨论了泊松公式在速度、加速度、坐标系和刚体运动描述中的应用。
1 泊松公式


2 径向速度和横向速度
在点的运动的描述中,位矢可以表示成位矢大小r和位矢方向单位矢量的积,即速度即:

式(2)中,第1项矢量的方向在位矢方向,称为径向速度,反映了位矢大小变化的快慢;第2项矢量的方向在垂直于位矢方向,称为横向速度,反映了位矢方向变化的快慢。
3 切向加速度和法向加速度
在点的运动的描述中,速度可以表示成速度大小υ和速度方向单位矢量的积,即速度其中方向变化的角速度可以用速度大小υ和轨道曲率半径ρ表示为且于是有:

式(3)中,第1项矢量的方向在速度方向,称为切向加速度,反映了速度大小变化的快慢;第2项矢量的方向在垂直于速度方向,称为法向加速度,反映了速度方向变化的快慢。
4 坐标系
直角坐标系选择了一组不随空间位置变化且相互垂直的单位矢量和在直角坐标系中,位矢表示成:


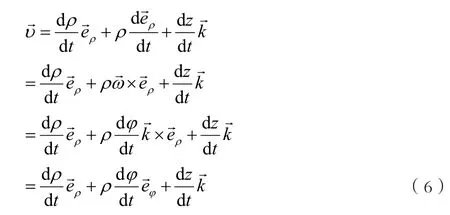




比较式(4)、(5)、(7)可知,位矢在直角坐标系中有3个不为0的投影,在柱坐标系中有2个不为0的投影,在球坐标系中仅有1个不为0的投影。在推导速度的式(6)和(8)时,运用了泊松公式。
5 刚体的运动
刚体是指在运动过程中,大小和形状变化可以忽略的物体。刚体上任意两点间的距离始终保持不变。描述刚体的运动,需要描述刚体上任意一点的运动。通常任意选择刚体上的一点A,则刚体上任意一点B的运动可以分解为A点的运动和B点相对于A点的运动的合成。因此,描述刚体的运动是一个相对运动的问题。


对于刚体的运动,A是刚体上的一点,B是刚体上的任意一点。由于刚体上任意两点间的距离始终保持不变,所以根据式(1),刚体的相对运动速度可以表示成:

将式(11)代入式(10)得,刚体上任意一点B的运动速度为:

6 结语
泊松公式是一个重要的矢量运算公式,在运动学中的速度、加速度的计算以及刚体运动的描述中有着广泛的应用。在柱坐标和球坐标系中计算速度,也运用到泊松公式,而且可以加深对坐标系的理解。不同的坐标系在本质上是选择一组相互垂直的单位矢量,任一矢量在某坐标系中,可以运用标题积得到投影表示形式。例如,一般地说,位矢在柱坐标系中有2个不为0的投影,当位矢在球坐标系中有1个不为0的投影;速度在柱坐标系和球坐标系中都有3个不为0的投影。运用泊松公式的计算,抽象简捷。
[1]范钦珊主编.理论力学[M].北京:高等教育出版社,2000.
