关于装配尺寸链计算的研究与分析

郭宵彬

（中车青岛四方机车车辆股份有限公司，山东 青岛 266111）

机械产品装配包括装配、调整、试验几部分，属于整个机械产品的最终环节，直接决定着机械产品的制作质量。产品的设计、制造环节需要对零件的尺寸、精度进行深入分析，因此，在整个机械产品的装配过程中，可以借助装配尺寸链评定、分析装配精度。

1 装配尺寸链的相关概述

1.1 装配尺寸链的定义

在机械产品、机械部件的生产、装配过程中，将对应的装配精度尺寸按照一定的顺序连接起来，组成一个全新、封闭的尺寸组，如图1所示。简单而言，装配尺寸链也可以称之为尺寸组，在实际的装配工作中，装配尺寸链的质量直接影响着机械产品的工艺、结构、组建质量、装配质量、精度等。只有加强平键与键槽的配合，按要求设计出间隙，就能够组建出新的装配尺寸链。

图1 为装配尺寸链的结构示意图

1.2 装配尺寸链构建方式

就实际的情况而言，装配尺寸链与工艺尺寸链两者之间的类似度较强，装配尺寸链的构建包括封闭环、组成环两部分。封闭环指的是在机械及其的生产、加工、装配中，能够间接的获取相应的尺寸，封闭环达到的精度是装配尺寸链，对装配技术有着重要要求，对应的是制造过程中的装配尺寸精度。在实际的装配过程中，装配的精度、尺寸、位置均会受到组成环的影响。封闭环之外的尺寸就是组成环，分为增环、减环两种，在装配尺寸链中组成环依据同向为减、异向为增的原理，能够迅速将组成环的性质辨别出来。

1.3 装配尺寸链的特点

（1）装配尺寸链内的封闭环必须要满足机器、零部件的要求，装入键槽内时，要保持一定的间隙。以此满足装配精度的要求，形成符合尺寸的封闭环。

（2）装配尺寸链中的封闭环不具备独立性，在装配结束之后，需要相关的零件保护才能够投入使用。

（3）装配尺寸链的组成环对装配精度有较高的要求，直接影响着零件、部件的尺寸，对位置的精准度也有影响。

2 装配尺寸链的计算

2.1 简单装配尺寸链计算

简单装配尺寸链分为极值法、概率法两种计算方法，在装配尺寸链的计算中，极值法、该算法的解算公式基本一致。在计算过程中，需要进行正面、中间、反面三项计算。就简单装配尺寸链的计算，本文重点探讨中间计算法，中间计算法装配尺寸链的计算公式如下。由于存在两种不同的计算公式，极值法、概率法，将已知条件代入公式中，遵守相关的计算依据，代入公式内得出平均公差计算公式。

式中TM为平均公差，m为增环数量，n为减环数量，T0为封闭环的公差值。

根据装配加工中的复杂程度，总结各项实践经验，将协调环确定。依据平均公差公式，计算出组成环的公差，以相关的算法标准为依据，标注式子中的偏差。极值法需要按照入体原则进行标注，概率计算法按照双向等偏差原则标注。将协调环的尺寸、公差、偏差计算出来，标注出协调环，能够参照相关的工艺将解算出尺寸链。

2.2 复杂装配尺寸链的计算

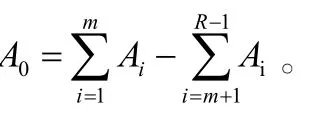
2.3 装配尺寸链协调环的选择原则

锁闭环的公差装配过程中需要按照相关的要求开展各项装配施工，以既定值为依据，在计算出了组成环公差之后，一些组成环的公差可能存在着较大的误差。简单而言，就是取定的组成环公差也不一定是标准公差值。针对存在误差的组成环，在装配尺寸链中承担着协调作用，这类组成环可作为协调环。依据公式装配链的上下偏差，将尺寸链的数值计算出来，进而确定精准度，将精准度的误差控制在相应的范围内。协调环的选择原则主要如下。

在工艺过程中应该尽量选择没有确定尺寸的刀具加工，将不需要使用极限量检验的尺寸作为协调环的尺寸。

尽可能选择加工简便的协调环，确保后期加工速度与质量。针对一些装配较难的尺寸公差，应该遵守从大到小的原则，科学、合理取值，按照从严到简的加工标准，将一些难以加工的作为协调环，以此确保尺寸公差的精准度。在协调环的选取中，标准件、公共环无法作为协调环，根据实际的施工情况而言，协调环的制造难度与其他组成环的制造难度相比，基本一致。

3 装配尺寸链计算的应用案例

本文的应用案例主要是以减速器的某轴结构尺寸 为 主， 其 中 A1=40mm、A2=36mm、A3=4mm。在装配结束之后，要求轮齿的端部间隙A0控制在0.10mm～0.25mm的范围内。若是采取完全互换装配方式，先要将A1、A2、A3的极限偏差值确定出来。首先需要对轴装配进行深入分析，明确在装配之后的齿轮端部的间隙A0就是封闭环。将A1、A2、A3组成环，绘制出相应的装配尺寸链示意图，如下图2所示。从装配尺寸链图中能够得知，A0在0.1～0.25的范围内，属于封闭环，A1属于增环，A2、A3属于减环。

3.1 极值法计算

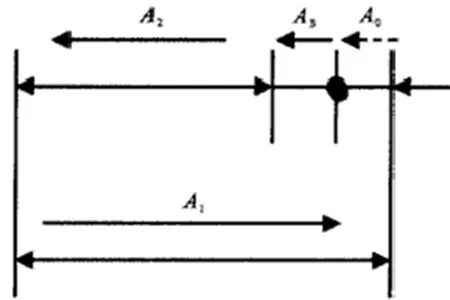
图2 为某对轴装配尺寸链结构示意图

在选择协调环时，应该考虑变速箱的壳体内部加工问题，因此，对精度的要求不高，进而在上述例子中，可以选择A1作为协调环。各个组成环的公差计算，首先需要分析各个尺寸，根据尺寸的大小，施工的复杂程度，T（A2）的取值为0.04、T（A3）的取值为0.02，则协调环的公差为 T（A0）=T（A1）+T（A2）+T（A3）。得出0.15=T（A1）+0.04+0.02，最终计算出答案T（A1）=0.09。零件的上下偏差，按照入体原则，得到A2=36（偏差为-0.04）°，A3=4°（偏差为-0.02）。协调环的上下偏差计算，依据上述尺寸链的计算公式，0.25=ES（A1）-（-0.04）-（-0.02）=0.1。EL（A1）=0.1，得到A1=40（误差范围为0.1～0.19）。

3.2 概率法计算

4 结语

综上所述，极值法是在极值的情况下，包含极大值与极小值两种情况，以精准度的要求为主，将组成环、封闭环之间的关系计算出来。通过本文的案例分析能够看出，这类计算方式简单，计算结果精准可靠。但是，如果封闭环的尺寸精度要求较高，组成环的数目过多，将会影响组成环公差的精准性，在公差上可能存在过大、精度过高的情况，增加了后期机械施工的难度。同极值计算法不同，概率计算法的核心属于公差范围中间部分零件。就零件而言，极限尺寸的零件数目较少，若是开展多环尺寸链装配工艺，极限尺寸的数量较少。因此，若是生产量过大，可以使用概率法计算尺寸链，进而降低制造成本。

[1]郑伟,马强.电机装配中轴向尺寸链的分析与计算[J].防爆电机,2017,52(05):126-128.

[2]张开富,杨海成,李原.装配尺寸链修配环最大修配量的分析与计算[J].机械设计,2015,25(03):223-224.