应用小生境和反向学习策略的量子粒子群算法
2018-03-01李志鹏李卫忠杜瑞超
李志鹏,李卫忠,江 洋,杜瑞超,刘 唐
(空军工程大学 a.研究生院; b.防空反导学院, 西安 710051)
粒子群优化算法(PSO)是一种广泛应用于工程领域优化求解的智能优化方法,与其他算法相比,简单易行,易于理解,但面临复杂的优化问题,基本粒子群算法存在早熟、易陷入局部最优和收敛速度慢等缺点[1]。针对这些问题,国内外学者对PSO算法做了很多研究,使算法性能得到优化,但对算法的易懂性、可操作性考虑较少。文献[2-3]将结合量子力学与粒子群算法结合,提出了一种以变量δ势阱为基础的算法模型——量子粒子群(quantum particl swarm optimization,QPSO)算法。与PSO算法相比,该算法有更好的全局搜索能力,但惯性权值线性递减的策略使算法仍易陷入局部极值,对于高维多极函数问题,算法在寻优能力、搜索精度、稳定性等方面有待改善。
本文提出一种应用小生境和反向学习策略的量子粒子群算法(quantum-behaved particle swarm optimization algorithm using niche and opposition-based learning,NOL-QPSO),以可拓理论为基础构造可拓粒子群算法模型,通过聚类在每代种群实现小生境的划分;结合个体适应度动态共享技术,有效解决算法过早收敛的问题,增强寻优能力;此外,针对最优粒子自我学习能力受限的缺点,引入精英反向学习策略,将算法拓展到当前种群以外的搜索空间,以增强解空间的开发。
1 量子粒子群算法
在量子粒子群算法模型中,粒子被赋予了量子行为,其状态通过波函数来描述。粒子在量子δ势阱的基础上不断向局部吸引点靠近,粒子出现在空间某一处的概率通过求解薛定谔方程得出,从而利用蒙特卡罗模拟更新粒子位置,其方程具体描述为:
(1)
(2)
其中G是最大迭代次数。
QPSO的算法流程如下:
1) 初始化粒子群;
3) 求出个体适应度值xi(g),并通过比较得到xi-best(g);
4) 更新xbest(k);
6) 位置更新:xi(g)=xi(g+1),g=g+1;
7) 重复2)至6),直到结束条件满足。
2 应用小生境和反向学习策略的量子粒子群算法
2.1 基于可拓理论的小生境构造策略
QPSO算法用于具有多个局部极值的复杂优化问题时,常常会出现收敛速度慢或早熟等问题,因此本文考虑通过小生境策略增强算法的全局性。小生境是源于生物学的一个概念[4],其基本思想是根据某种规则把种群划分为若干子种群,各个子种群动态形成相对独立的搜索域,从而在各搜索域对解空间内不同的局部最优点展开同步搜索,完成最终优化,避免了过早收敛或不同个体在同一空间出现过度搜索现象。该技术要考虑的关键问题之一是小生境的划分,常用的方法是通过设定小生境半径划分子空间,这种方法虽简单可行,但对于复杂问题的求解效果并不理想。本文以物元可拓理论[5]为基础,采用可拓聚类算法构造小生境。
2.1.1 基本知识
设Q(k)=Xi,i=1,2,…,N}为含有N个样本的初始种群,每个样本特征维数为n,样本I的数据模型可表示为
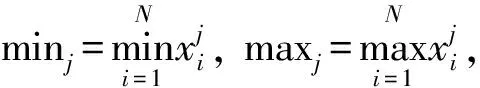
定义1Xi对类Sl的关联度Kx(Sl)计算准则定义为
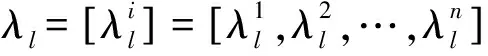

定义3 当l=Γ时,Ro与类SΓ的关联度则为类SΓ的自关联度,可表示为
式中:nΓ是类SΓ的样本数目;Ki(SΓ)是类SΓ第i个样本的关联度。
2.1.2 小生境构造方法
步骤1 随机选取k个待聚类样本作为中心,形成k个初始类Sl,(l=1,2,…,k)。
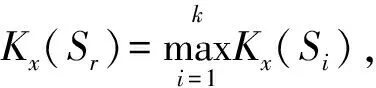

步骤4 聚类调整完成后,更新各类中心物元,重新计算关联度,重复新一轮的样本归类,直至归类结果不变。
通过以上基于可拓理论的聚类过程,形成稳定多样的小生境,各子种群在相对独立的空间寻优,可以避免粒子群陷入局部极值,增强算法的全局性。
2.2 适应度共享和精英反向学习策略
在粒子群优化算法中,距最优点越近的粒子,其位置更新越会受到较大限制,导致粒子群只能在局部极值邻域进行搜索,这是使粒子陷入局部最优和影响算法寻优精度的主要因素之一。因此,可以考虑通过强化精英粒子邻域的搜索,优化算法性能。为提高算法的搜寻能力,本文在小生境技术的基础上,在算法中引入共享函数和精英反向学习策略。
共享函数[6]最先用于遗传算法中个体间相邻关系的度量。文献[7]在粒子群算法中引入共享函数,当搜索陷入局部最优时,将种群划分为两部分,其中一部分继续对局部最优进行搜索,而另一部分则重新初始化,并通过定义共享适应度函数对寻优范围加以限制,当个体再次陷入早熟区,则适当增大其适应度,促使粒子逸出。
引入共享函数,首先需要对个体相似度进行度量,常用的方法是利用hamming距离对个体进行度量。在进化算法中,hamming距离可以反映不同个体基因编码间存在的差异,也可以对种群多样性做出判断。本文考虑以hamming距离为依据,选取距局部最优解较近的粒子,对适应度进行调整,从而能跳出早熟区做进一步寻优。但在迭代过程中,适应度更新后的个体可能会再次陷入原早熟区。为有效解决这一问题,本文利用共享距离D划定共享区,提出一种适应度动态共享策略,对共享区内个体的适应度进行调节。
设在某次迭代中,含有若干粒子的群体收敛于Xlocal-best,个体i到Xlocal-best的距离用di表示,则:
(3)

(M为常数)
(4)
其中:dnew为新粒子距局部最优解Xlocal-best的距离;M为修正权值,可根据实际情况调整值的大小。不难看出:dnew越小,粒子距局部最优解越近,为其赋予越大的适应度,能够使个体以更大概率突破局部限制,避免新群体再次陷入局部最优。
另外,在量子粒子群算法中,全局最优粒子往往会包含更多引导种群向全局最优收敛的价值信息,对种群的进化方向具有重要的引导作用。最优粒子在当前种群中的自我学习能力受限,会影响算法的全局搜索能力,因此有必要拓展到当前种群以外的搜索空间对全局最优粒子进行深度挖掘。本文考虑引入精英反向学习策略,粒子群每达到一定迭代次数,对全局最优粒子进行一次反向学习,增强解空间的开发,提高算法精度。

(5)
精英反向粒子的引入,有效拓展了搜索空间,在一定程度上打破原小生境,促进种群进化。在本文算法中,利用迭代次数确定精英反向粒子的引入时机,即每迭代N次,算法进行一次精英粒子反向学习,保证在一定概率范围内引导种群向更优位置进化。
3 仿真实验与结果分析
算法性能的优劣主要体现在寻优精度和收敛速度上。为评估算法性能,本文参照文献[7]选取CEC2005 benchmark测试函数,分别对PSO算法、QPSO算法、文献[9]提出的CLQPSO算法及本文的NOL-QPSO算法进行测试。实验操作在 Intel(R) Core(TM) i7-4790 CPU@ 3.60 GHz计算机平台上,利用64位Windows 7操作系统中的MATLAB 2014软件编程实现。
测试函数如表1所示。Sphere函数为单峰曲面函数,其最小值0在零点取得;Rosenbrock函数是一个多峰值函数,其全局最优点在(1,1,…,1)取得,处于一个狭长、平滑的抛物线山谷内;Schaffer函数是复杂的二维函数,在解空间里有无数个极小值点,具有强烈的震荡性;最小值0在(0,0)处取得,对其全局最优值的搜索难度较大;Rastrigrin函数和Griewank函数都是典型的非线性多模态函数,峰形高低起伏呈跳跃性。其中,Griewank函数搜索空间较广,极小值的数目与维数有关,是优化算法常用的测试函数。Ackley函数是由数函数叠加适度放大后的余弦得到的连续性函数,余弦波的调制在相对平坦的曲面形成波峰,优化算法对其寻优时易陷入局部最优。
实验结果如表2所示。由表2可见:PSO算法在运行中常陷入局部极值,其性能在几种算法中是最差的;与PSO相比,QPSO算法的收敛速度明显加快,但仍易陷入局部最优,搜索性较差;CLQPSO算法采用Levy概率分布的飞行策略,扩大了搜索空间,搜索到全局最优解的概率较高,但收敛速度有待改善。NOL-QPSO算法在大多数情况下表现良好,在寻优精度上,除了Schaffer函数、Rosenbrock函数的最差值和Griewank函数的最优值次于CLQPSO算法外,其余各值均优于其他算法。另外,NOL-QPSO算法搜索到全局最优解的概率明显提高,到达门限值的平均迭代次数更少。从算法的平均运行时间来看,本文提出的算法与其他算法差别不大,在允许范围内取得了更好的优化效果。

表1 测试函数
表2 实验数据
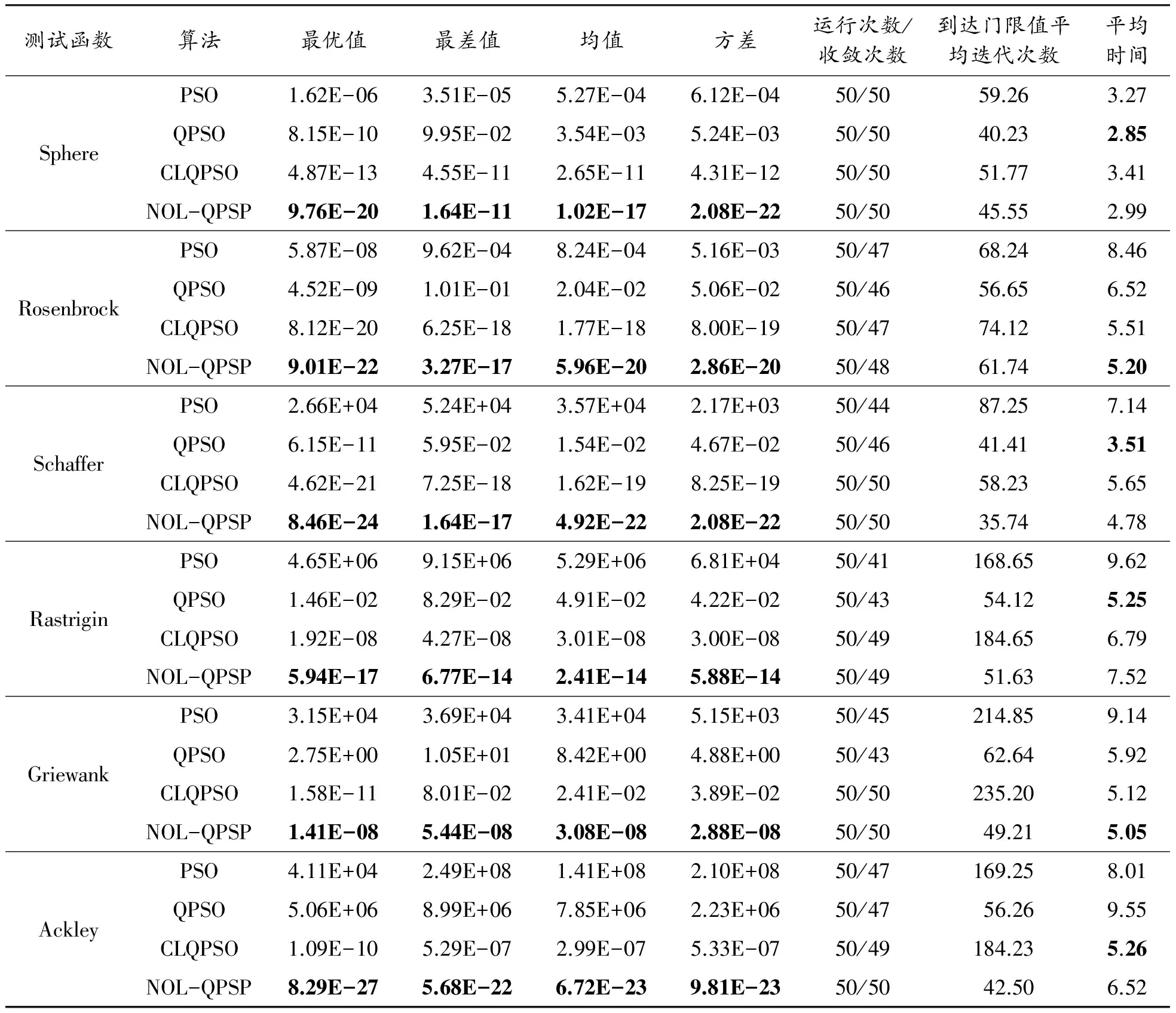
测试函数算法最优值最差值均值方差运行次数/收敛次数到达门限值平均迭代次数平均时间SpherePSO1.62E-063.51E-055.27E-046.12E-0450/5059.263.27QPSO8.15E-109.95E-023.54E-035.24E-0350/5040.232.85CLQPSO4.87E-134.55E-112.65E-114.31E-1250/5051.773.41NOL-QPSP9.76E-201.64E-111.02E-172.08E-2250/5045.552.99RosenbrockPSO5.87E-089.62E-048.24E-045.16E-0350/4768.248.46QPSO4.52E-091.01E-012.04E-025.06E-0250/4656.656.52CLQPSO8.12E-206.25E-181.77E-188.00E-1950/4774.125.51NOL-QPSP9.01E-223.27E-175.96E-202.86E-2050/4861.745.20SchafferPSO2.66E+045.24E+043.57E+042.17E+0350/4487.257.14QPSO6.15E-115.95E-021.54E-024.67E-0250/4641.413.51CLQPSO4.62E-217.25E-181.62E-198.25E-1950/5058.235.65NOL-QPSP8.46E-241.64E-174.92E-222.08E-2250/5035.744.78RastriginPSO4.65E+069.15E+065.29E+066.81E+0450/41168.659.62QPSO1.46E-028.29E-024.91E-024.22E-0250/4354.125.25CLQPSO1.92E-084.27E-083.01E-083.00E-0850/49184.656.79NOL-QPSP5.94E-176.77E-142.41E-145.88E-1450/4951.637.52GriewankPSO3.15E+043.69E+043.41E+045.15E+0350/45214.859.14QPSO2.75E+001.05E+018.42E+004.88E+0050/4362.645.92CLQPSO1.58E-118.01E-022.41E-023.89E-0250/50235.205.12NOL-QPSP1.41E-085.44E-083.08E-082.88E-0850/5049.215.05AckleyPSO4.11E+042.49E+081.41E+082.10E+0850/47169.258.01QPSO5.06E+068.99E+067.85E+062.23E+0650/4756.269.55CLQPSO1.09E-105.29E-072.99E-075.33E-0750/49184.235.26NOL-QPSP8.29E-275.68E-226.72E-239.81E-2350/5042.506.52
4 结束语
本文以可拓理论为基础构造算法模型,结合适应度动态共享和精英反向学习策略,提出一种改进的粒子群算法——NOL-QPSO。
1) 以可拓理论为基础,将小生境策略用于量子粒子群算法,以改善算法的全局性。
2) 加入适应度动态共享环节,通过引入共享函数调整适应度,避免陷入早熟。
3) 通过测试函数实验,验证了本文所提算法的有效性。
本文算法表现出较好的性能,具有较强的适应能力,全局搜索性更加优越。对运行效率的改善,将是后续研究的重点之一。
[1] 任俊亮,邢清华,李强,等.采用自适应概率粒子群算法的反导预警资源调度方法[J].空军工程大学学报(自然科学版),2014,15(6):45-48.
[2] SUN J,FENG B,XU W B.Particle swarm optimization with particle having quantum behavior[C]//Proceedings of Congress on Evolutionary Computation.Portland,USA:IEEE Press,2004:325-331.
[3] SUN J,XU W B,FENG B.Adaptive parameter control for quantum behaved particle Swarm optimization on individual level[C]//Proceedings of IEEE International Conference on Systems,Man And Cybernetics.Piscataway:IEEE Press,2005:3049-3054.
[4] 付强,王刚,王明宇,等.基于小生境遗传算法的制导雷达误差估计[J].空军工程大学学报(自然科学版),2011,11(06):50-53.
[5] 杨春燕,蔡文.可拓学[M].北京:科学出版社,2014.
[6] 张珂,黄永峰,李星.一种基于适应度和节点聚类的P2P拓扑建模方法[J].电子学报,2010,38(7):1634-1640.
[7] 谭熠峰,孙婷婷,徐新民.基于动态因子和共享适应度的改进粒子群算法[J].浙江大学学报(理学版),2016,43(6):696-700.
[8] 邵鹏,吴志健,周炫余,等.基于折射原理反向学习模型的改进粒子群算法[J].电子学报,2015,43(11):2137-2144.
[9] 陈伟,周頔,孙俊,等.一种采用完全学习策略的量子行为粒子群优化算法[J].控制与决策,2012,27(5):719-723.
