采用Melnikov方法的齿轮传动系统的分岔及混沌分析
2018-03-01周杜,乐源
周 杜,乐 源
(西南交通大学 力学与工程学院, 成都 610031)
齿轮机构被广泛应用于机械系统当中,是机器产生振动和噪音的主要来源之一,所以对齿轮系统振动特性的研究具有重要的理论及现实意义。国内外许多学者[1-3]对齿轮系统的非线性特性进行了大量的研究,结果表明:系统表现出了丰富的动力学特性,如分岔和混沌。王建军[4]深入研究了系统参数振动的主要特征。唐进元[5]利用图胞映射方法对单自由度非线性齿轮系统进行了全局特性分析。苏程[6]研究了单对齿轮系统随参数变化时的频响规律。卫一多[7]考虑了摩擦作用下周期双参变激励齿轮系统。王晓笋[8]对含磨损故障的齿轮传动系统进行了非线性动力学特性研究。李应刚[9]利用增量平衡法研究了外部动态激励作用下齿轮系统的动力学响应。A.Farshidianfar[10]利用Melnikov方法对非线性齿轮系统中混沌状态进行了解析预测和控制。
本文考虑了含齿侧间隙、时变啮合刚度和综合啮合误差等因素下的单自由度齿轮传动模型,以分岔与混沌作为非线性现象的分析手段,在文献[10]的基础上利用Melnikov方法对系统同宿轨线出现分岔及马蹄混沌[11]的参数区域进行预测,给出系统随参数变化的最大李雅普诺夫指数图。结合相轨线、庞加莱截面对系统的动力学响应进行分析,并和Melnikov方法预测的系统出现同宿分岔和混沌的参数区域进行对比。
1 含间隙齿轮传动模型

图1 齿轮副动力学模型
如图1所示,单对齿轮间隙非线性动力学模型考虑了时变刚度、齿侧间隙、粘弹性阻尼和外部激励力等因素,不考虑齿轮传动时的横向运动,其运动只有扭转运动。不考虑运动时由支承轴承所产生的摩擦的影响。其中:θi(i=1,2)为主被动齿轮的扭转角位移;Ii(i=1,2)为主被动齿轮的转动惯量;rbi(i=1,2)为主被动齿轮的基圆半径;c为齿轮副的啮合阻尼;e(τ)为齿轮啮合综合误差;k(τ)为齿轮副的啮合综合刚度;Ti(i=1,2)为作用在主被动齿轮上的转矩;mi(i=1,2)为主被动齿轮的质量。
利用牛顿定律可得到系统的运动微分方程:
(1)
引入齿轮啮合线的相对位移坐标x=rb1θ1-rb2θ2-e(τ),将式(1)中的方程组化简得到系统的相对扭转方程:
(2)

(3)
间隙分段线性函数为:
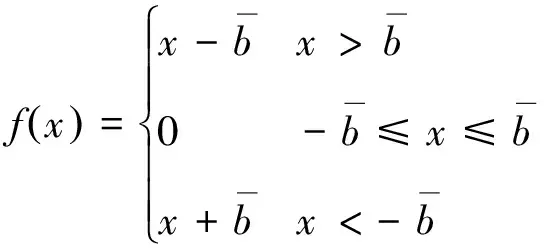
(4)
若刚度和啮合综合误差均取1阶谐波分量,则有:
(5)
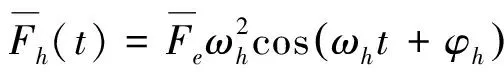
(6)
2 Melnikov分析
Melnikov方法可用来解析地判定拟哈密顿系统出现Smale意义上的混沌。如果一个Hamilton系统存在同宿或异宿轨道,考虑弱的周期性扰动,使其对应的周期轨道的不动点的稳定流形和不稳定流形分裂,可用Melnikov积分来判定两流形之间的距离。如果这个距离有简单的零点,则可判定系统存在Smale马蹄意义上的混沌。本文将通过引入小参数ε构造出拟Hamilton系统,并用Melnikov方法进行求解。
(7)
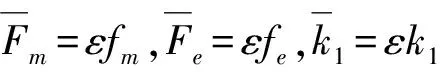
(8)
其中a=c=0.166 7。令ε=0,获得对应的Hamilton系统的同宿轨道为
(9)
(10)

(11)
将式(10)代入式(11)得:

(12)
整理可得:

(13)
如果M±(t0)具有简单零点,则系统的稳定流形和不稳定流形横截相交,即方程(8)存在Smale马蹄意义上的混沌。
3 数值模拟
令M±(t0)=0,取fe为控制参数。依据Melnikov函数理论,系统产生混沌的必要参数条件为:
(14)
(15)
固定参数值ε=0.01,ωh=1,k1=6,fm=10,可将式(14)(15)写为:
fe(1)>2.345ζ1+1.1555
(16)
fe(2)<-2.345ζ1-1.1555
(17)
由式(16)(17)得到两条分界线L1、L2如图2所示。当系统参数取分界线L1上方的区域A2或者分界线L2下方的区域A3时,系统同宿轨线发生横截相交,将出现马蹄混沌;当位于分界线L1、L2所夹的A1区域时,系统为周期运动。

图2 系统同宿轨出现马蹄混沌的参数区域
对于一个系统是否出现混沌,目前一个公认的标准就是系统的李雅普诺夫指数。总体来说,李雅普诺夫指数是系统任意相邻轨线平均发散或收敛程度的一种度量,是目前判断混沌运动最可靠的一种定量的方法。本文将在Jacobi方法[12]的基础上,直接利用李雅普诺夫指数的定义,计算系统的最大李雅普诺夫指数及第二李雅普诺夫指数,并将计算的结果与庞加莱截面进行比较。
为验证上面的分析结果,将式(3)转化为状态方程:
(18)
其中,
(19)
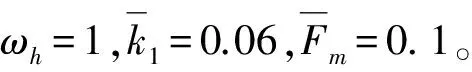

图3 内部误差激励力
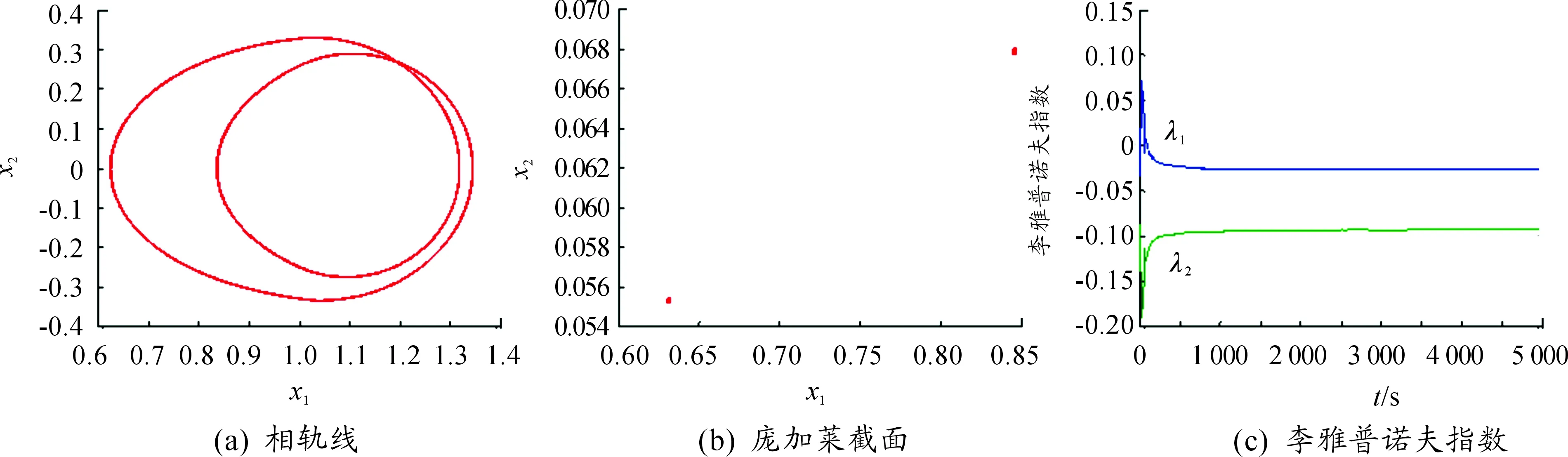
图4 内部误差激励力
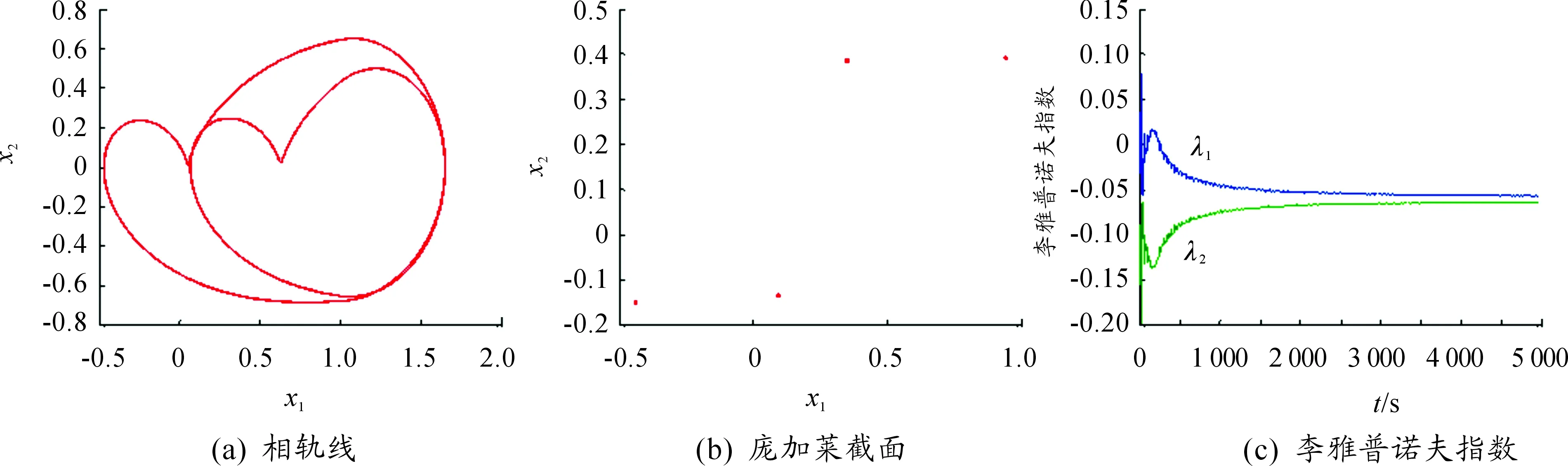
图5 内部误差激励力
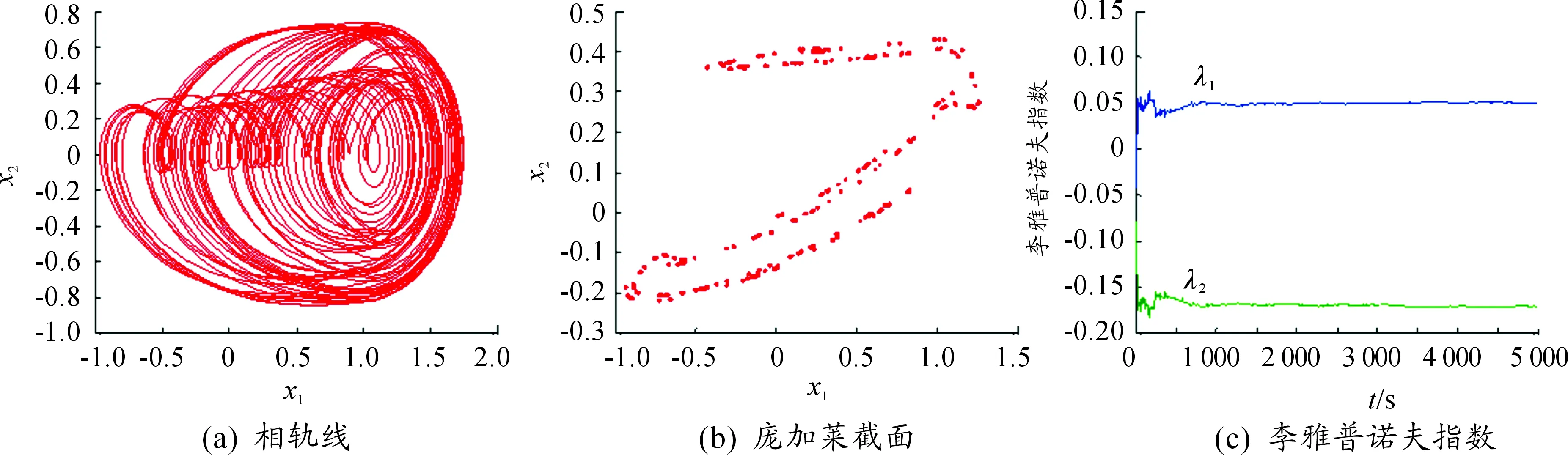
图6 内部误差激励力

图7 内部误差激励力
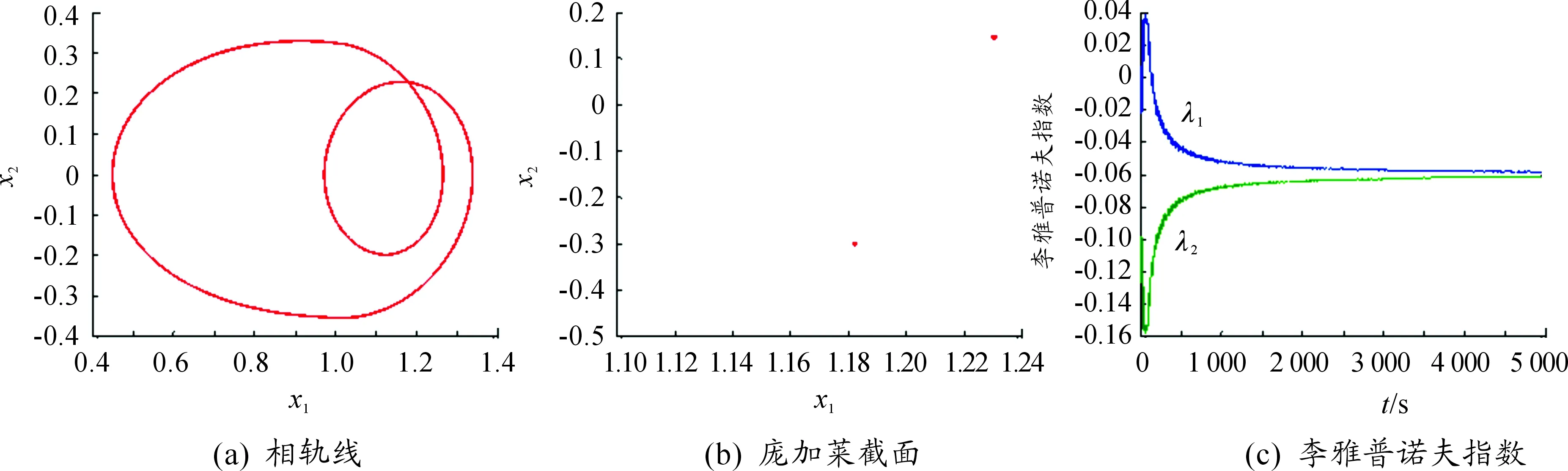
图8 内部误差激励力
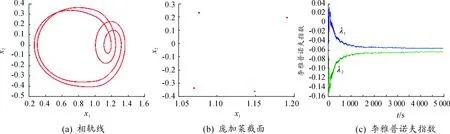
图9 内部误差激励力

图10 内部误差激励力

图11 系统随内部误差激励力变化的分岔图和李雅普诺夫指数图
4 结束语
利用Melnikov方法对单自由度齿轮系统同宿轨线出现分岔及马蹄混沌的参数区域进行了预测。利用变步长Runge-Kutta法对系统进行了数值求解,给出了系统随内部误差激励力变化的分岔图以及最大李雅普诺夫指数图,并结合相轨线、庞加莱截面分析了内部误差激励力变化时系统复杂的动态响应。
Melnikov方法预测的系统出现同宿分岔及马蹄混沌的参数区域和数值模拟的结果基本吻合,表明在一定的参数范围内,随着内部误差激励力的变化,系统通过倍化分岔进入混沌运动。
在工程实际当中,结合系统同宿轨线出现分岔及马蹄混沌的参数区域,选择合适的参数取值范围能有效地控制系统的碰撞行为,使其不会产生混沌激励,确保齿轮系统保持稳定运行状态,减少对齿轮机构的磨损,保障齿轮系统更加安全有效地工作。
[1] KAHRAMAN A,SINGH R.Non-linear dynamics of a spur gear pair[J].Journal of sound and vibration,1990,142(1):49-75.
[2] 李润方,王建军.齿轮系统动力学[M].北京:科学出版社,1997.
[3] 王三民,沈允文,董海军.含摩擦和间隙直齿轮副的混沌与分叉研究[J].机械工程学报,2002,38(9):8-11.
[4] 王建军,韩勤锴,李其汉.参数振动系统频响特性研究[J].振动与冲击,2010,29(3):103-108.
[5] 唐进元,熊兴波,陈思雨.基于图胞映射方法的单自由度非线性齿轮系统全局特性分析[J].机械工程学报,2011,47(5):59-65.
[6] 苏程.单级齿轮传动系统非线性动力学特性分析[J].兰州理工大学学报,2012,38(1):32-36.
[7] 卫一多,刘凯,崔亚辉,等.摩擦作用下周期双参变激励齿轮系统非线性振动响应研究[J].中国机械工程,2012,23(4):289-294,442.
[8] 王晓笋,巫世晶,周旭辉,等.含磨损故障的齿轮传动系统非线性动力学特性[J].振动与冲击,2013,32(16):37-43.
[9] 李应刚,陈天宁,王小鹏,等.外部动态激励作用下齿轮系统非线性动力学特性[J].西安交通大学学报(自然科学版),2014,48(1):101-105.
[10] FARSHIDIANFAR A,SAGHAFI A.Identification and control of chaos in nonlinear gear dynamic systems using Melnikov analysis[J].physics letters A,2014,378(46):3457-3463.
[11] DU Z,ZHANG W.Melnikov method for homoclinic bifurcation in nonlinear impact oscillators[J].Computers & Mathematics with Applications,2005,50(3/4):445-458.
[12] WOLF A,SWIFT J B,SWINNEY H L,et al.Determining Lyapunov exponents from a time series[J].Physica D:Nonlinear Phenomena,1985,16(3):285-317.
