基于对称相关谱和累积量切片的QAM信号识别

王燚婷，高 勇

(四川大学 电子信息学院，四川 成都 610065)

0 引言

随着无线通信技术的快速发展，调制识别被广泛应用在电子对抗、电子侦察和光谱监测等多种军用和民用场合。由于高阶QAM信号具有较高的频谱利用率，在卫星通信以及微波通信技术中得到广泛应用。因此，对M-QAM信号的正确识别就显得极其重要。

基于特征提取的模式识别方法有很多种，主要包括基于瞬时统计量信息特征的调制识别[1-2]、基于高阶累积量的调制识别[3-4]和基于谱线特征的调制识别[5-6]等。目前针对QAM信号的识别方法也有很多种。基于似然函数的识别方法性能最佳，文献[7]提出了基于平均对数似然函数的方法对M-QAM信号进行分类，但基于似然函数的方法需要知道码速率、载波频率以及采样率等先验信息，并且计算复杂度较高不利于工程实践。文献[8]采用高阶累积量对数字调制信号进行识别，抗噪性能较好。基于循环统计量[9]和循环谱[10]的调制识别算法虽然具有良好的抗噪声性能，并且不受载波残余影响，但所需要的码元个数以及采样点数数目较大。文献[11-12]利用聚类算法提取特征，完成对64阶以下M-QAM的识别。基于聚类的识别算法，虽然能区别高阶QAM信号，但是当阶数较高(M>64)时识别效果不佳，并且聚类中心较多使得计算量过大，不利于实时处理。文献[13]基于改进的HY-NCMA盲均衡方法识别多径环境中的高阶QAM信号，信噪比在18 dB以上时识别率达到90%以上。文献[14]通过估计调制信号的载频、带宽以及波特率重构M-QAM信号矢量图，并根据矢量图中最小环带方差完成识别，但是随着QAM阶数的提高，需要较多的码元长度。

基于信号谱分析的调制识别，无需任何的先验信息，提取出的特征参数比较稳定。范海波[15]等基于信号的谱线特征对卫星通信中的常见信号进行了识别，但是在信噪比较低的情况下，有价值的谱线信息往往被噪声淹没而降低识别率。文献[16]利用八阶累积量，对16QAM和64QAM信号进行了识别，能识别的高阶QAM信号数量较少。文献[17]针对M-QAM信号的四次方谱线特征将信号分为{16QAM，64QAM}和{32QAM，128QAM}两类，但当信噪比低于10 dB时识别率较差。为了解决上述问题，本文基于信号四次方的对称相关谱和四阶累积量的切片值[18]特征，提出了一组无需知道先验知识并且对调制参数以及信噪比变化不敏感的特征参数，对经过NI USRP-2930的{16QAM、32QAM、64QAM、128QAM}实测信号进行了识别。识别结果表明，所提出的参数具有较好的稳健性，并且该算法具有较好的识别性能。

1 四次方谱与四次方对称相关谱

正交幅度调制是一类应用广泛的幅相结合调制方式，其一般模型可以表示为：

(1)

式中，g(t)为基带成型脉冲，通常采用升余弦型脉冲；周期为T；an和bn分别为基带信号的I路和Q路数据。对于符号序列等概率且以原点对称分布的QAM信号而言，其二次与四次方形式的统计期望为：

(2)

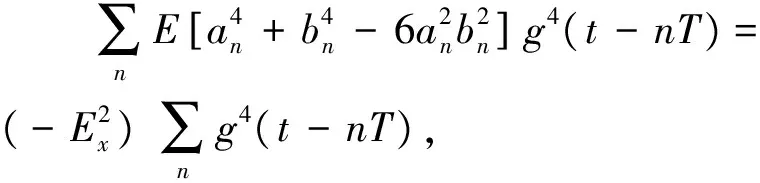
(3)

式中，Ex代表信号x(t)的能量；T为信号x(t)的周期，计算其四次方谱[19]可得：

(4)

式中，

A(f)=F[g4(t)]=G(f)*G(f)*G(f)*G(f)，F[g4(t)],

表示对g4(t)求傅里叶变换，G(f)是g(t)的傅里叶变换结果，*表示线性卷积。由于在高阶QAM信号中，G(f)的非零频域范围为[-(1+α)/2T，(1+α)/2T]，则A(f)的非零频域范围为[-2(1+α)/T，2(1+α)/T]，成型滤波器系数α取值通常为0.3～0.5，这使得n的范围限制在{0，±1，±2}，所以V(f)只有在频率为{0，±1/T，±2/T}处出现谱线，并且A(f)的幅度随频率衰减速度至少为f-4，所以f=±2/T处的谱线强度远远小于频率{0，±1/T}处的谱线强度。

依据上述理论，计算4种信号的四次方谱。星座图呈方形的16QAM和64QAM信号的频谱中具有明显的离散谱线；而对于星座图呈十字形的32QAM和128QAM信号，其频谱中虽然存在离散谱线，但是强度明显降低。4种QAM信号在信噪比为5 dB时的四次方谱谱线图如图1所示。

图1 M-QAM信号的四次方谱

由图1可知，在信噪比较低的情况，16QAM和64QAM的部分离散谱线被淹没，谱线特征难以提取，这将使得对信号的识别效果不佳。因此本文引入了一种噪声抵消方法——对称相关函数法。下面分析对称相关函数抵消的机理。

设x(t)为实信号。对称相关函数的定义[20]为：

(5)

式中，T为信号周期。由式(3)和式(5)得到高阶QAM信号四次方的对称相关，

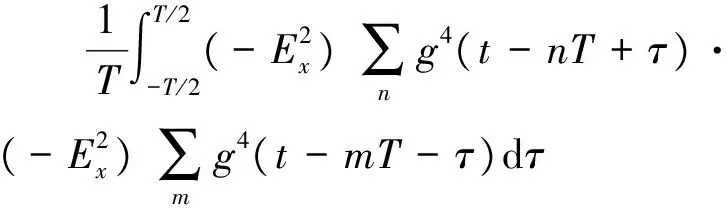
(6)

对式(6)做傅里叶变换得到对称相关谱，

V(f)=F{E[Sx4(t)]}=

(7)

同样地，A(f)非零区间的限制使得n和m的取值得到限制。当τ=nT且τ=-mT，即n=m=0时，f在零频处存在谱线且谱线强度至少为A2(0)。而且V(f)的幅度衰减速度至少为f-8，比A(f)的衰减大很多，因此经过对称相关处理后的谱线相比四次方谱，前者在非零频点处的衰减更大。

假设接收信号为s(t)，则s(t)=x(t)+n(t)，其中n(t)是均值为0、方差为σ2的高斯白噪声，且x(t)和n(t)相互独立，于是s(t)的对称相关函数为:

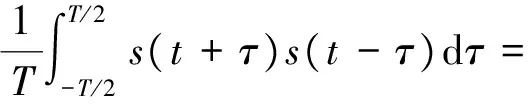
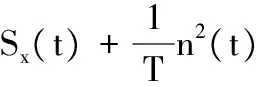
(8)

从式(8)可以看出，T取得越长，Ss(t)受噪声的影响越小。相比原始信号s(t)，进行对称相关运算后抵消了一部分与信号不相关的加性噪声。因此，在对M-QAM信号识别之前，对信号的四次方进行对称相关运算后再提取谱线特征，能更好地抑制噪声。文献[20]还给出了计算离散序列的对称相关函数Ss(j)，

(9)

式中，j=0，1，2，…，J-1；N为数据长度，满足2L+J≤N；L为对称相关窗的长度。对于32QAM和128QAM信号，由于二者的四次方谱线不明显，而对称相关仅是对噪声进行抑制，对信号本身的谱线影响甚微，所以对称相关处理后依然没有明显的谱线，只是幅度有所增强；而16QAM和64QAM四次方谱存在谱线，对称相关处理后谱线在频点f=0处更加突出。16QAM和64QAM在信噪比为5 dB时信号四次方谱和四次方对称相关谱的仿真结果如图2所示。

图2 16QAM和64QAM的四次方谱和对称相关谱对比

2 高阶QAM信号的四阶累积量切片

x(t)为平稳随机过程，其K阶累积量[21]的定义为:

Ckx(τ1，τ2，…，τk)=Cum(x(t)，x(t+τ1)，…，x(t+τk-1))，

(10)

式中，Cum(τ)的含义为对τ求累量，τ1，τ2，…，τk为x(t)任意滞后值。则其四阶累积量的表达式为:

Ckx(τ1，τ2，τ3)=Cum(x(t)，x(t+τ1)，x(t+τ2)，x(t+τ3))。

(11)

假设信号的数据长度为N，对离散信号的四阶累积量一维切片的短时估计方法如下[22]：

① 将N个样本划分为K段，记为Sk(0)，Sk(1)，…,Sk(M-1)，每段包含M个数据。

② 估计每段M个数据的三阶累积量值，

S(k)(n+τ2)S(k)(n+τ3)，

(12)

式中，k=1，…，K，M1=max(0，τ1，τ2，τ3)，M2=min(M-1，M-1-τ1，M-1-τ2，M-1-τ3)。

③ 计算1～K各段的四阶累积量的平均值，作为该接收信号的四阶累积量的估计值。令τ=τ1=τ2=τ3，得到信号四阶累积量的一维切片值：

(13)

由于零均值的高斯随机信号或过程的四阶累积量值为零，因此该一维切片值具有很强的高斯噪声抵消能力。4种QAM信号经过归一化后的四阶累积量的一维切片值如图3所示。

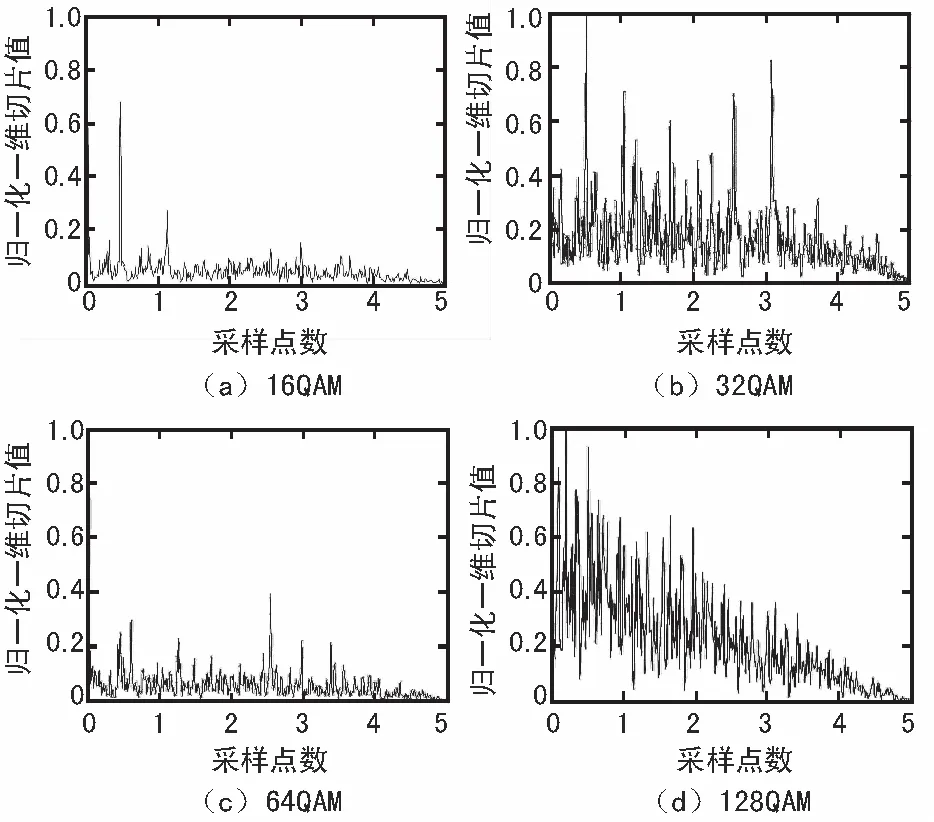
图3 M-QAM信号四阶累积量的一维切片

3 特征参数的选取

特征参数的提取与计算是调制识别的关键，在选取特征参数的时候应该考虑该参数的鲁棒性，这样才能在较低信噪比的环境下具有较好的识别效果。本文提出了3个对信噪比和调制参数顽健性好的特征参数。

由于16QAM和64QAM的对称相关谱的最大谱线强度明显大于与之相邻的最大谱线强度，而32QAM和128QAM的对称相关的最大谱线突出程度不明显，根据这一特点可以定义参数Fn，表示信号对称相关谱的最大值与其相邻左右最大谱线和次大谱线之和的比值。若调制信号的四次方对称相关谱用Sx表示，并且定义

P0=max(|Sx|)，

P1=max(|Sx(1∶ind-1)|)(ind为P0的横坐标)，

P2=max(|Sx(ind+1∶end)|)(ind为P0的横坐标)，

P3=max(|Sx(1∶ind1-1)|)(ind1为P1的横坐标)，

P4=max(|Sx(ind2+1∶end)|)(ind2为P2的横坐标)，则特征参数Fn表达式为：

(14)

该参数用于描述最大谱线的突出程度，理论上能将信号分为{16QAM，64QAM}和{32QAM，128QAM}两类。

由图3中16QAM和64QAM的四阶累积量一维切片值，可以看出16QAM具有较大的峰值，根据这一特征构造参数C4max，

C4max=max(Y{Ck(τ)})，

(15)

式中，Y{Ck(τ)}表示归一化后的信号四阶累积量一维切片峰值。该参数能够较好地区别16QAM和64QAM。然后观察32QAM和128QAM的切片值，可以看出128QAM的谱峰近似呈线性递减的趋势，因此可以考虑构造一个线性递减函数，并计算该函数与切片值的欧氏距离。基于此特点提出特征参数C4s，其计算如下：

① 先对信号归一化四阶累积量一维切片值进行中值滤波

S(n)=Med{Ck(n-v)，......Ck(n-1)，

Ck(n)，Ck(n+1)，......Ck(n+v)}，

(16)

式中，n∈N，N是待识别信号的长度；Med{}表示对内部元素排序并求中值，每次抽取元素个数m=5，则v=(m-1)/2。

② 构造线性单调递减序列

(17)

式中，R表示对S(n)求最大值；N为待识别信号的长度。

③ 为了衡量S(n)与线性递减函数的相似度，此处利用2-范数计算S(n)与T(n)的欧式距离：

C4s{S(n)，T(n)}= ‖S(n)-T(n)‖2=

(18)

特征参数C4s能够表征S(n)和T(n)的相似度，计算结果越小，说明二者相似度越高。对于128QAM信号，由于S(n)与T(n)的相似度更高，理论上其C4s应小于做相同处理后32QAM的C4s。

4 算法验证

本文采用半实物仿真验证，利用NI USRP-2930产生并接收{16QAM，32QAM，64QAM，128QAM}四种信号，并利用LabVIEW对接收的数字调制信号进行下变频处理以获得所接收调制信号的基带信号。设定发送端载波频率为915 MHz，码元速率为100 kbps，采样率为400 kHz，滚降系数为0.35。

4.1 实验1：特征参数随信噪比变换情况的研究

待识别的信号集包括{16QAM，32QAM，64QAM，128QAM}四种信号，加入的噪声为仿真高斯白噪声，信噪比范围为0～30 dB，每个识别样本取10 000个样本点。特征参数Fn，C4max以及C4s随信噪比变化的曲线如图4、图5和图6所示。

不同信噪比情况下参数Fn的值，显示了噪声对特征参数Fn的影响，如图4所示。由图4可以看出，参数Fn的值较为稳定。由于16QAM和64QAM的谱线比较突出，所以其特征参数在信噪比大于5 dB时明显大于32QAM和128QAM的特征参数值，证明利用特征参数Fn可以将信号分为{16QAM，64QAM}和{32QAM，128QAM}两类。

图4 Fn随SNR分布曲线

不同信噪比情况下参数C4max的值如图5所示，显示了噪声对特征参数C4max的影响。由图5可知，16QAM和64QAM的特征值都比较稳定，二者随信噪比变化波动不大。其中16QAM的特征C4max的值稳定在0.6和0.7之间，而64QAM的特征C4max的值稳定在0.35和0.4之间。所以该参数能有效区分16QAM和64QAM，由此证明了特征参数C4max的合理性。

图5 C4max随SNR变化曲线

不同信噪比情况下参数C4s的值如图6所示。

图6 C4s随SNR变化曲线

由图6可知，128QAM信号C4s明显小于32QAM信号的C4s值，同时128QAM的特征C4s的值在0.4和0.6之间波动。而32QAM的特征C4s在信噪比较低时波动较大，在大于15 dB时该值稳定在1.2左右。所以利用C4s可以对32QAM和128QAM两种信号进行有效的区分，证明了参数C4s的可行性。

4.2 实验2：识别性能的研究

在上述实验的基础上，在相同信噪比环境下对每个信号独立进行100次蒙特卡洛实验，得到不同信噪比下(1 dB为步长)4种调制信号的识别率。信噪比在0～30 dB时4种信号的识别率曲线如图7所示。由识别率统计结果可知，当信噪比为0 dB时，能较好地识别32QAM和128QAM信号，而无法识别出16QAM和64QAM信号。4种信号的识别率随SNR的增加而增加，均可达到100%。

图7 识别率统计结果

另外，由于信号的特征参数会受码速率的影响而造成一定的波动。在采样率和采样点数相同的条件下，码速率不同，信号的识别率将有所不同。为了验证本文特征参数的鲁棒性，下面将研究4种信号在不同码速率的情况下的识别率。固定信噪比为7 dB，各个信号在不同码速率下的识别率如表1所示。

表1 信噪比为7 dB时信号在不同码速率下的识别率(%)

码速率/(bit/s)调制类型16QAM32QAM64QAM128QAM100k10010098100500k10010099100800k100100981001M100100971002M9910098100

结果表明，不同码速率的情况，对4种信号的识别率影响不大，并且4种信号的识别率均达到了97%以上。进一步说明本文提出的特征参数具有较好的稳定性，利用这些特征参数进行识别性能比较突出。

5 结束语

本文在高阶QAM四次方谱线特征的基础上提出了信号四次方的对称相关谱，但是仅根据该谱线特征对调制信号进行识别是远远不够的，因此引入了高阶累积量，利用四阶累积量的切片特征与对称相关谱特征相结合的混合识别算法实现对高阶QAM信号的识别。文中待识别信号采用实测信号，算法复杂度低，具有较好的工程使用价值。实验结果表明，在信噪比大于7 dB时识别率达到97%以上，验证了本文的算法具有实用性和有效性。

[1] 王志力，王玉文，蒋瑜，等.基于决策理论的信号调制识别改进算法[J].无线电工程，2014，44(5)：30-33.

[2] 曾旭，慕晓冬，易昭湘，等.基于改进的瞬时信息量数字调制识别算法[J].无线电工程，2016，46(12)：21-25.

[3] 吕新正，魏平，肖先赐.利用高阶累积量实现数字调制信号的自动识别[J].电子信息对抗技术，2004，19(6)：3-6.

[4] 韩钢，张文红，李建东，等.基于高阶累积量和支撑矢量机的调制识别研究[J].系统工程与电子技术，2003，25(8)：1007-1011.

[5] 杨琳，许小东，路友荣，等.基于谱线特征的恒包络数字调制方式识别方法[J].中国科学技术大学学报，2009，39(9)：936-943.

[6] 吕平，高勇.一种CPM信号与PSK类信号的调制识别算法[J].无线电通信技术，2015，41(4)：64-67.

[7] LONG C S，CHUGG K M，POLYDOROS A.Further Results in Likelihood Classification of QAM Signals[C]∥ Military Communications Conference，Milcom’94 Conference Record，IEEE，1994：57-61.

[8] 包锡锐，吴瑛，周欣.基于高阶累积量的数字调制信号识别算法[J].数据采集与处理，2010，25(5)：463-467.

[9] 赵春晖，杨伟超，马爽.基于广义二阶循环统计量的通信信号调制识别研究[J].通信学报，2011，32(1)：144-150.

[10] 赵雄文，郭春霞，李景春.基于高阶累积量和循环谱的信号调制方式混合识别算法[J].电子与信息学报，2016，38(3)：674-680.

[11] LI Y L，LI B B，YIN C Y.Modulation Classification of MQAM Signals Using Particle Swarm Optimization and Subtractive Clustering[C]∥ IEEE International Conference on Signal Processing，2010：1537-1540.

[12] YANG F，LI Z，LI H，et al.Method of Neural Network Modulation Recognition Based on Clustering and Polak-Ribiere Algorithm[J].Journal of Systems Engineering and Electronics，2014，25(5)：742-747.

[13] 王彬，葛临东.基于盲均衡的高阶QAM信号调制识别算法[J].电子与信息学报，2007，29(8)：1882-1886.

[14] 张路平，王建新.MQAM信号调制方式盲识别[J].电子与信息学报，2011，33(2)：332-336.

[15] 范海波，杨志俊，曹志刚.卫星通信常用调制方式的自动识别[J].通信学报，2004，25(1)：140-149.

[16] LIU L，XU J.A Novel Modulation Classification Method Based on High Order Cumulants[C]∥ International Conference on Wireless Communications，NETWORKING and Mobile Computing，2006：1-5.

[17] 徐江民，高勇.高阶QAM信号调制识别算法[J].无线电工程，2014，44(1)：32-35.

[18] 柯宏发，陈永光，张哲峰.基于四阶累积量对角切片的短波自适应通信信号检测[J].电子学报，2006，34(3)：419-423.

[19] 杨琳，许小东，路友荣，等.常见数字通信信号的谱线特征分析[J].电子与信息学报，2009，31(5)：1067-1071.

[20] 樊养余，陶宝祺，熊克，等.基于对称相关函数法的谐波信号重构[J].信号处理，2001，17(5)：400-405.

[21] WANG X，GUO Q，LI Q，et al.High-order Cumulant-based Adaptive Filter Using Particle Swarm Optimization [C]∥ IEEE，Control and Decision Conference，Ccdc，2008：4567-4570.

[22] SATTAR F，SALOMONSSON G.On Detection Using Filter Banks and Higher Order Statistics[J].IEEE Transactions on Aerospace & Electronic Systems，2000，36(4)：1179-1189.