自由运动曲率公式修整——《自由运动论》在实际中的应用(30)

咸立德

(曲阜市书画社，山东 曲阜 273100)

本文以人造卫星发射为例，对万有引力公式加以修正，以及对自由运动论所描述的规律加以综合性修整，整理后，使《自由运动论》具有一个较为完美的自由运动规律的描述以及较为完整的自由运动曲率公式。公式可适用于宏观和微观领域的自然规律的相关预测。

一、关于万有引力公式的修正

卫星圆周运动的向心力由引力提供的公式推导中可以看出，公式体现的是卫星发射到进入轨道正常运行时的预测轨道半径。

卫星在脱离地球表面到预定轨道绕地球做圆周运动时，地球质量应该是地球原始质量M减去卫星质量m，而公式确还是用的地球发射卫星之前的原始质量，从理论的严格来考虑，万有引力公式在实际应用推导中，地球质量必须修正为M-m。

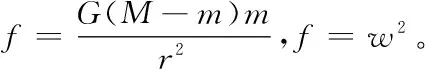
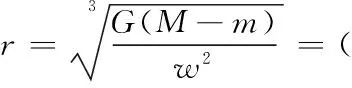
由原来的引力公式中可知，卫星轨道半径与卫星质量无关。而由修正后的(1)式可以看出，卫星质量和卫星轨道存在关联性，而且有：卫星质量越大，卫星轨道半径越小的规律，这样既符合万有引力定律的描述，也和《自由运动论》所描述的物体运动曲率和质量成正比的理论是一致的。

二、自由运动曲率公式修整

在《自由运动论》中只是分章节分别描述了物体运动曲率和几个物理量的关系。如果综合起来考虑的话，可以总结为：物体的运动曲率(K)和物体质量(K)成正比，和物体密度(ρ)成正比，和物体自转速度(W)的平方成正比，和运动速度(V)的平方成反比。

三、圆周运动和自由运动曲率公式的关系

实际上，自由运动曲率公式也无非就是从多个物理量对运动的影响的角度上描述了物体做圆周运动的规律。其中部分规律是可以等效于现有的圆周运动规律的。就是在不考虑物体自转速度、密度对曲率的影响，只考虑运动速度时，曲率运动公式中的运动速度对运动的影响，也可以等效于圆周运动的速度对运动的影响。由圆周运动规律可知：

则：v=wr。

把v=wr带入(2)式。

公式表明，只有当物体的自转速度和公转角速度相等时，同时不考虑质量及其密度对运动的影响时，曲率公式才完全等效于传统的圆周运动公式。

把(1)式带入(3)式。

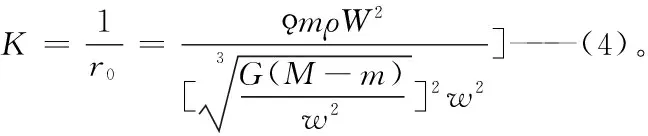
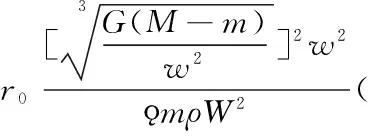
(3)、(4)式是经过部分物理量和圆周运动等效，即只考虑轨道速度(运动速度)的作用下圆周运动的等效性，同时考虑了物体质量、密度、自转速度对运动曲率的影响时的自由运动的较为严谨的自由运动曲率公式表达。

公式(4)表明，当卫星的自转速度和公转角速度相等时，其自转速度不影响轨道半径，只有卫星质量及其密度会影响到卫星轨道半径，也就是卫星质量和密度与轨道半径成反比。和(1)式相比，(5)更为严格地存在质量和轨道半径成反比的关系。就是说，万有引力定律及其公式，只粗略的符合物体的自转速度和公转角速度相等时的特殊情况。可在自然规律中，这种天体的自转速度和公转角速度相等的现象极其罕见。导致引力定律的适用范围很小的根本原因，是定律及其公式中没考虑物体的自转速度及其密度等对运动的影响的结果。

四、万有引力公式修正和自由运动曲率公式修整的意义

(一)在发射卫星问题上的指导意义

以上理论表明，按《自由运动论》的理论，由于卫星轨道半径和卫星质量成反比，所以卫星放入轨道后，较大质量的卫星会因为轨道半径较小向着较小轨道上漫漫演化，甚至出现重新掉落到地面上的情况。所以，即便仍然按现有的引力公式来发射卫星，如果发射质量较大的卫星，实际卫星高度要比预测的高度要高，这样在经过演化后，轨道半径变小也不至于出现重新掉落到地面上的情况。

(二)对地球表面自由落体的同时性问题的纠正

在《关于自由落体的探讨》一文中，只从《自由运动论》的理论作为基础，分析了同等高度的质量大的物体先落地的原理。

事实上，地球表面附近的物体在做自由落体时，除了高度很小以外，其性质也无异于卫星释放到预定轨道后的性质，同样可以遵守引力作用下的圆周运动性质，就是在自由落体仍然可以依据修正后的公式(1)来判定物体的落体轨道半径等物理量。同样可以表明，质量较大的物体的落体(运动)轨道半径较小，落体轨道曲率较大，相对于地面观察者的加速度就较大。所以相对于地面观察者，同等高度的物体在自由落体时，质量大的先落地才是符合客观规律的。也是和《关于自由落体的探讨》的理论相符合的。也就是说，引力公式的不严谨性，不仅仅误导了卫星轨道与质量的关系，也误导了地球表面附近的同等高度的自由落体现象中的落地加速度与质量的关系。

(三)曲率公式修正对微观领域的实用性

本文对引力公式进行修正，以及建立了一个较为完整的自由运动曲率公式后，公式(4)和(5)也是可以应用到微观领域的。就是结合《论光的可变性》及《红移现象的形成原理》，公式可以预测光粒子在大尺度上的公转轨道半径，就是相当于，即便是像发射卫星一样发射一个质量极小的光粒子，公式也可以成立。同样也可以预测光粒子在碰撞中产生巨大自转速度，运动曲率急剧增大而形成复粒子后的极小的轨道曲率及曲率半径。

五、曲率公式在不同维度上的应用

(一)原始质量和星系的虚空中心的关系

以地球系为例，公式可以分别推算地球和月球在地球系里的公转轨道。结合《<自由运动论>的宇宙学原理》第四节的论述，一个较小的天体绕着一个较大的天体公转是相对的，事实上都是绕着一个虚空的中心在公转而已。这个虚空的中心就是原始质量天体的存在时的位置。就是月球无异于在原始天体上人工发射了一个巨大的人造卫星。如图所示：

设原始天体质量为M0。膨胀分裂出一个月球后的地球质量为M，月球质量为m(M0=M+m)。

设：地球的运动曲率为K，月球运动曲率为k。

公式(6)(7)分别表达了地球和月球再地球系中的运动性质，地球和月球的距离是r-R。

(二)曲率公式在不同维度上的应用

公式(6)、(7)只是描述了地球和月球在地球系中的运动性质，根据《《N维空间论》续》的理论，要考虑在更高维度上的太阳系里的运动性质。就要考虑整个地球系的运动性质。比如地球系的自转速度是由地球和月球在地球系里的公转角速度来决定。运动速度要考虑地球系绕太阳的公转速度，质量也是要考虑地球和月球的总质量等。如果把地球在地球系的运动视为一维运动，那么，地球在太阳系中就是二维运动。单独考虑地球(或者月球)在太阳系里的二维运动性质会较为复杂，比如地球的二维上的自转速度应该是地球在地球系里的公转角速度等。

本节继续以数学原理，利用自由运动曲率公式表达了星系都具有一个虚空的中心的客观事实。也就是说，通过对《自由运动论》理论中的自由运动曲率公式的修整，公式基本可以描述宏观和微观的运动规律。

六、结论

[1]咸立德.略论《自由运动论》的哲学性[C].2016首届全国智慧城市建设应用高峰论坛论文集，2016.

[2]咸立德.自由运动论[C].2016首届全国智慧城市建设应用高峰论坛论文集，2016.