基于改进FMEA法的深基坑施工风险评价
2018-03-01王倩露林慧龙王洪强
程 敏, 王倩露, 林慧龙, 王洪强
(上海大学 管理学院, 上海 200444)
随着高层建筑和地下工程的发展,深基坑在工程中应用越来越广泛。由于深基坑工程施工环境复杂、技术难度大、不可预见因素多,使得深基坑施工事故常发,不仅造成工期延误、人员伤亡,也产生了巨大经济损失和不良社会影响。因此,开展深基坑施工风险分析和评估,把握关键风险点,对保障深基坑工程顺利进行至关重要。深基坑施工风险已引起了学者们的关注,例如:刘俊伟等[1]采用模糊综合评判法建立深基坑施工风险评价模型;夏元友等[2,3]基于现场检测对深基坑施工风险进行动态评估;杜修力等[4,5]构建基于证据理论的风险评价模型;魏道江等[6]建立基于投影寻踪及信息扩散的深基坑施工风险动态评价方法。这些研究有助于管理者把握深基坑施工风险程度,但多侧重于深基坑工程的整体水平评价,所采用的方法在对各风险事件的重要性分析方面还存在一定的局限。深基坑施工风险管理有必要识别出诸多风险因素中的关键风险,以便于重点关注和采取有针对性的措施进行防控,提高工程的安全性。
失效模式和影响分析(Failure Modes and Effect Analysis,FMEA)是一种用于分析潜在失效模式及影响的方法,近年来也被一些学者用于风险分析[7~9]。FMEA法将风险发生的频度O、严重度S、难检度D三项相乘得到风险顺序数RPN,根据RPN大小来判断风险因素的重要性。但是,传统FMEA在实际运用中存在一定局限性。一方面,运用FMEA法评价风险时,需依赖专家的知识和经验进行数值化打分。然而,不同专家进行评价时使用的评估术语可能不同,也可能会用不同刻度标准的数字和语义描述评价结果,这种多粒度问题会导致评估信息存在一定的不确定性和不完整性,不利于准确判断各风险因素的主次关系。另一方面,传统的FMEA法通过对O,S,D三个属性值简单相乘得到RPN,忽略了三者的相对重要性,并且O,S,D的不同组合可能产生完全相同值的RPN,但它们所代表的风险影响却可能是完全不同的[10,11]。因此,有必要对传统FMEA方法进行改进。
关于FMEA法中语言评价信息的处理问题,主要有两种改进方法:基于扩展原理的分析方法和基于符号转移的方法[12]。基于扩展原理的分析方法是先将评价语言信息转化为模糊数,再进行模糊数运算和去模糊化,如Liu等[9,13~14]均使用模糊理论来处理专家的语言评价信息。基于扩展原理的方法需要决策者确定评价语言集的隶属度函数,在分析中可能会产生信息的丢失和扭曲。而基于符号转移的方法则是直接对语言评价信息进行运算或处理,往往只能得到近似的结果,可能与最初的评价信息不一致[15]。为了克服这两类方法的不足,西班牙学者Herrera等[16]基于符号转移的概念提出了二元语义表达模型,先将决策者的评价信息转化为二元语义符号,再进一步进行处理,从而避免语言评价信息集结和运算中的信息失真,提升计算精度和可靠性。
关于传统FMEA法中通过O,S,D三个属性值简单相乘确定风险排序这一方式的不足,国内外学者提出了多种方法来加以改进:一类是数学规划的方法,如数据包络分析(Data Envelopment Analysis,DEA)[17],线性规划法[18];另一类是多准则决策方法,如决策试验与试验评估法(Decision Making Trial and Evaluation Laboratory,DEMATEL)[9]、逼近理想解排序法(Technique for Order Preference by Similarity to an Ideal Solution,TOPSIS)[19]等。本文则拟采用灰色关联分析进行风险排序,该方法计算简便,不需对原始数据进行归一化处理,且无需大量样本,也无需数据满足相应的分布规律,具有普遍适用性。它常被用于决策问题中,通过计算各方案的评价向量与理想最优方案的评价向量间关联度的大小来确定方案优劣排序[20]。
综上,本文将建立基于二元语义和灰色关联分析的改进FMEA法,在运用二元语义将专家团队对各风险事件做出的语言评价信息转化为数学语言的基础上,应用灰色关联分析法确定各风险的优先度排序,从而合理地评估深基坑施工风险。
1 二元语义及相关定义
二元语义指通过一个二元组(s,α)来表达决策者的语言评价信息,其中s是预定义语言术语集S的一个语言术语,α为符号转移值。一个二元语义可以表示为(si,αi),si∈S,其中si表示第i个语言术语的中心值,αi为评价结果与第i个语言术语中心值的偏差。下面定义二元语义及相关运算符号。
定义1:设S={s0,s1,...,sg}为一个语言术语集,S中的元素数目g+1称为语言术语集的粒度。β∈[0,1]表示语言术语集通过集成得到的实数。β可由转化函数Δ转化为二元语义符号[21],即:
(1)

(2)
式中:round为四舍五入取整算子。
定义2:设(si,α)是一个二元语义,则存在一个反函数Δ-1,能将其转换成相应的数值,即:
(3)
(4)
一般地,一个二元语义是由一个语言术语增加一个0值作为符号转化而来的,即:
si∈S⟹(si,0)
(5)
在二元语义的运算中,函数Δ和函数Δ-1的共同运用可以确保二元语义在转化过程中没有信息丢失。对于任意两个二元语义符号(si,α1)和(sj,α2),它们的比较有如下规则:(1)当i


(6)
2 基于二元语义和灰色关联分析的改进FMEA方法

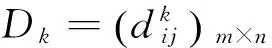
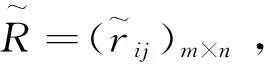
(7)
(8)
一般将通过式(7)得到的二元语义综合判断矩阵作为比较序列。
步骤3:确定参考序列,并建立距离矩阵。在FMEA方法中,结果越小意味风险越小。因此,参考序列中语言术语所表示的各项风险因素都应为最低值,其二元语义形式为(s0,0),即参考序列为:
r0=(r0j)1×n=[(s0,0),(s0,0),…,(s0,0)]
(9)

步骤4:计算风险因子的权重。对各风险因子的聚合权重(wj,αwj)进行归一化,即:
(11)

(12)
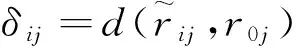
根据灰色关联系数,并考虑各风险指标的权重,可进一步计算各风险事件的灰色关联度φi:
(13)
步骤6:确定风险事件的排序。灰色关联度φi越小,风险事件的危害就越大。因此,可根据φi的大小对影响深基坑施工的风险事件进行排序。
3 深基坑施工风险评估的应用实例
3.1 项目概况

3.2 深基坑施工风险评价指标体系
该项目深基坑施工主要包括桩基、支撑、开挖、降水4大分项工程,因此本文从这4方面识别项目深基坑施工风险。依据JGJ 311-2013《建筑深基坑工程施工安全技术规范》等相关规范,并结合项目特点,采用德尔菲法建立该项目深基坑施工风险清单,如表1所示。
3.3 风险评估
本文邀请了5位深基坑施工领域的专家组成FMEA评估小组,基于上述改进FMEA法,对该项目深基坑施工过程中的风险事件进行评估。为保证专家评价结果的合理性,本文邀请的5位专家均具有10年以上深基坑工程经历,有丰富的深基坑施工经验,熟悉深基坑施工技术,并且具有高级职称;同时5位专家均具有本科以上学历,以保证能够较好地理解本文采用语言术语集的形式来表达自己判断的方法。根据不同专家的经验和知识差异,5名专家在此次评价中的相对权重分别设为:0.2,0.25,0.3,0.15,0.1。
(1)定义语言术语集和语言判断矩阵。5位专家采用不同的粒度构建各风险事件O,S,D的语言术语集,分别为:
T1={a0=非常低(VL),a1=低(L),a2=中等(M),a3=高(H),a4=非常高(VH)};
T2={b0=非常低(VL),b1=低(L),b2=略低(ML),b3=中等(M),b4=略高(MH),b5=高(H),b6=非常高(VH)};

表1 A项目深基坑施工风险清单
T3={c0=极其低(EL),c1=非常低(VL),c2=低(L),c3=略低(ML),c4=中等(M),c5=略高(MH),c6=高(H),c7=非常高(VH),c8=极其高(EH)};
T4={d0=非常低(VL),d1=低(L),d2=中等(M),d3=略高(MH),d4=高(H),d5=非常高(VH)};
T5={e0=非常低(VL),e1=低(L),e2=略低(ML),e3=中等(M),e4=略高(MH),e5=高(H),e6=非常高(VH)};
专家对于O,S,D的相对重要程度的评价则采用如下语言术语集:
F={f0=非常不重要(VU),f1=不重要(U),f2=中等(M),f3=重要(I),f4=非常重要(VI)}。
FMEA专家依据以上语言术语集对所有风险事件的各风险因子及其相对权重进行语言评价,并将其转化为二元语义,分别如表2,3所示。

表2 FMEA专家团队二元语义评价矩阵

表3 风险因子二元语义权重
(2)聚合各专家的评价信息,构建一个群的综合判断矩阵。采用式(7)聚合专家对各风险因子的二元语义权重判断,结果如表4所示。
(3)确定参考序列,计算距离矩阵。在FMEA中,较小的值意味着越少的风险。因此,参考序列被设定为r0=(rO,rS,rD)=[Δ(0),Δ(0),Δ(0)]。用式(10)计算比较序列和参照序列间的距离,结果如表4所示。

表4 群的综合判断矩阵和风险因子权重聚合
(4)采用公式(11)对表4中风险因子的聚合权重进行归一化处理,并采用公式(12)计算各风险事件各风险因子的灰色关联系数,结果如表5所示。

表5 灰色关联系数和标准化后的风险因子权重
(5)采用式(13)计算各风险事件的灰色关联度,根据灰色关联度确定各风险事件的重要性排序结果,如表6所示。从表6的风险排序可以看出,该深基坑施工的关键性风险事件主要是支护施工时未按设计要求进行R10、支撑变形过大R9、桩位测量不准R3、电焊机等机械设备漏电R8等,这些事件大多属于支撑施工。施工管理者应对这些关键风险进行分析并制定相应的风险防控措施。

表6 风险事件的灰色关联度和风险优先度
4 结 论
本文建立了一种结合二元语义和灰色关联分析的改进FMEA法评估深基坑施工风险,从而发现诸多风险事件中的关键风险。所提出的改进FMEA方法具有以下优点:
(1)采用二元语义及其集结算子集结处理语言评价信息,可以有效避免传统语言信息处理方法中所出现的信息失真问题,提高评价结果的准确性。
(2)考虑了风险因子的相对权重,且风险因子和它们的相对重要性通过语言方式来评价,而不是精确的数值进行评估。这使专家们可以更真实地表达自己的判断,增加了FMEA的适用性。
(3)该方法考虑了专家不同的决策特征,允许不同专家使用不同粒度的语言术语集来表达他们的判断。
(4)采用灰色关联分析进行风险排序,使结果更为合理,相对传统FMEA方法而言,避免了不同风险因子组合产生相同RPN值的问题。
运用该方法对深基坑施工风险开展分析,有助于管理者识别各类风险的重要性程度,从而有针对性地采取相应措施,减小风险。该方法直观、可操作性强,为多属性决策问题提供了新的思路,对于其他领域的风险评价也有一定的应用价值。
[1] 刘俊伟, 尚文昌, 于秀霞, 等. 基于模糊评判理论的深基坑施工风险评价[J]. 地下空间与工程学报, 2016, 12(3): 825-830.
[2] 夏元友, 陈春舒, 陈金培, 等. 基于现场监测的深基坑施工动态风险评估[J]. 地下空间与工程学报, 2016, 12(5): 1378-1384.
[3] 王 飞, 宋学文, 赵会艳. 基于现场监测数据分析的深基坑安全风险评价体系[J]. 公路, 2016, (11): 11-16
[4] 杜修力, 张雪峰, 张明聚, 等. 基于证据理论的深基坑工程施工风险综合评价[J]. 岩土工程学报, 2014, 36(1): 155-161.
[5] 程鸿群, 佘佳雪, 袁 宁, 等. 深基坑工程施工过程风险综合评价[J]. 同济大学学报(自然科学版), 2016, 44(3): 491-498.
[6] 魏道江, 李慧民. 运用投影寻踪及信息扩散理论评价深基坑施工风险[J]. 中国安全科学学报, 2015, 25(2): 147-152.
[7] 王晓暾, 熊 伟. 基于DLOWG算子的FMEA风险评估方法[J]. 浙江大学学报(工学版), 2012, 46(1): 182-188.
[8] Chang K H, Cheng C H. A risk assessment methodology using intuitionistic fuzzy set in FMEA[J]. International Journal of Systems Science, 2010, 41(12): 1457-1471.
[9] Liu H C, You J X, Lin Q L, et al. Risk assessment in system FMEA combining fuzzy weighted average with fuzzy decision-making trial and evaluation laboratory[J]. International Journal of Computer Integrated Manufacturing, 2015, 28(7): 701-714.
[10]Zhang Z, Chu X. Risk prioritization in failure mode and effects analysis under uncertainty[J]. Expert Systems with Applications, 2011, 38(1): 206-214.
[11]Gargama H, Chaturvedi S K. Criticality assessment models for failure mode effects and criticality analysis using fuzzy logic[J]. IEEE Transactions on Reliability, 2011, 60(1): 102-110.
[12]鲍广宇, 连向磊, 何 明, 等. 基于新型语言评估标度的二元语意标度的二元语意改进模型[J]. 控制与决策, 2010, 25(5): 780-784.
[13]Chanamool N, Naenna T. Fuzzy FMEA application to improve decision-making process in an emergency department[J]. Applied Soft Computing, 2016, 43: 441-453.
[14]Silva M M, de Gusmão A P H, Poleto T, et al. A multidimensional approach to information security risk management using FMEA and fuzzy theory[J]. International Journal of Information Management, 2014, 34(6): 733-740.
[15]张 震, 郭崇慧. 一种基于二元语义信息处理的多属性群决策方法[J]. 控制与决策, 2011, 26(12): 1881-1885.
[16]Herrera F, Martinez L. A 2-tuple fuzzy linguistic representation model for computing with words[J]. IEEE Transactions on Fuzzy Systems, 2000, 8(6): 746-752.
[17]Netto T A, Honorato H J, Qassim R Y. Prioritization of failure risk in subsea flexible pipes via data envelopment analysis[J]. Marine Structures, 2013, 34: 105-116.
[18]Wang Y M, Chin K S, Poon G K K, et al. Risk evaluation in failure mode and effects analysis using fuzzy weighted geometric mean[J]. Expert Systems with Applications, 2009, 36(2): 1195-1207.
[19]Song W, Ming X, Wu Z, et al. Failure modes and effects analysis using integrated weight-based fuzzy TOPSIS[J]. International Journal of Computer Ntegrated Manufacturing, 2013, 26(12): 1172-1186.
[20]刘思峰, 杨英杰, 吴利丰. 灰色系统理论及其运用(第7版)[ M]. 北京: 科学技术出版社, 2014.
[21]Tai W S, Chen C T. A new evaluation model for intellectual capital based on computing with linguistic variable[J]. Expert Systems with Applications, 2009, 36(2): 3483-3488.
[22]Liu H C, Li P, You J X, et al. A Novel Approach for FMEA: Combination of Interval 2-Tuple Linguistic Variables and Gray Relational Analysis[J]. Quality and Reliability Engineering International, 2014, 31(5): 761-772.
