基于安全的轻武器射击场防弹构件优化改造探析
2018-03-01赵梓翔
赵梓翔,王 征,荀 平
(解放军后勤工程学院, 重庆 401331)
随着部队军事训练日益频繁,射击场周边的安全问题,越来越被人们重视。据报道,2016年9月12日,南京某小区一位女士在散步时被流弹击伤,这颗流弹来自附近一处轻武器射击场。而这样的流弹袭击并非第一次发生,附近小区的一些业主及其车辆此前多次被流弹击中,流弹伤人事件引发了社会广泛关注。如何确保射击场周边的安全已成为部队轻武器射击场建设改建中亟待解决的问题。
1 射击场安全概况
大部分轻武器射击场在建造前都经过合理地规划选址,远离市区,有些巧借地形或者构建高大的挡弹墙来防止子弹飞出射击场。但是这些安全防护措施都具有局限性:规划选址可以避开高压线、交通要道和居民区,但是无法避开人们无处不在的活动,而且远离营区的射击场也给训练造成不便;利用山势或者构建挡弹墙可以阻挡子弹,但是这种措施受地形地貌的限制,而且防护效果有限。例如高度为15 m挡弹墙,只能阻挡从射击位射出发射角在9°以内的子弹,但是发射角大于9°的子弹仍然对周围造成威胁。总之,规划选址和构筑挡弹墙等措施无法满足部队对安全的要求。
相比部队射击场远离营区、市区,北京射击馆(见图2)、伦敦射击馆(见图3)等国际射击比赛场馆却建在城市内部。因为它们通常在射击区构筑靶挡、围墙和挡弹板等防弹构件来确保安全。这种措施安全可靠,同时还具有造价便宜、方便操作、便于修建、靠近城市的优点。部队对现有的射击场进行安全防护功改造,可以借鉴这种形式。

图1 传统射击场的安全隐患

图2 北京射击馆

图3 伦敦射击馆
2 射击场安全防护设计思路
与国际射击比赛场馆相比,部队射击场要相对简单,比如观众席、运动更衣室、办公附属用房部分的设计可以不考虑。根据部队射击训练习惯,训练人员进入射击待命区领取弹药,而后来到射击位装填子弹,听到指挥口令后完成射击动作(见图4)。射击位是指射手进行射击活动的规定位置[1]。因此要避免子弹飞出射击场伤人,就应该围绕射击位设置防弹构件。防弹构件是射击地线与目标之间上空和目标之后设置的阻挡子弹飞出的设施[2],它包括3部分:① 在射击位上方构建防弹顶棚;② 在射击区中间构建多段挡弹梁;③ 在射击场两边、后边构建挡弹墙。顶棚、挡弹梁和挡弹墙的组合,可以阻挡从射击位向前射出的子弹,确保子弹无法飞出射击场。
防弹构件的设计,主要考虑顶棚、挡弹梁和挡弹墙之间的数量、位置关系。通过弹道射线的分析计算,在适当的位置布置防弹构件确保射击场的绝对安全;并且通过控制所有防弹构件的防弹面积减少建筑材料的使用,从而降低成本。
Matlab是一个功能强大的常用数学软件,它可以解决计算问题,并且能够方便地绘制出各种函数图形[3]。
射击场防弹构件改造的内容就是研究子弹在场地内外的伤害范围,以及通过设置防弹构件阻挡子弹伤害[4-9]。因此,运用Matlab计算射击场弹道射线中数学问题,将防弹构件中数据进行量化分析,优化射击场安全防护改造方案。

图4 射击场训练流程

图5 射击场安全防弹构件示意图
3 射击场安全防护的改造方案研究
3.1 实例研究
以某部队营区内射击场改造为例(图6),该射击场较为简单,四面由围墙围合,后面挡弹墙高度较高。

图6 某部队需要改建的射击场
为方便分析计算,首先将改造方案的模型进行简化(图7):

图7 射击场简化模型剖立面图
1) 通过弹道射线分析,可知卧姿射击最不利于防弹构件的设置,假设射击点距地面高度近似为0;
2) 射击区的防弹构件由顶棚、n段挡弹梁、末端挡弹墙以及两侧挡弹墙组成;
3) 在不影响使用功能的前提下,顶棚高度越小,对防弹构件设置越有利,所以顶棚及挡弹梁净高高度取最小值 2.2 m[4];
4) 为方便施工或模块化配装,假设所有挡弹梁高度一致,其上部梁高度为h;
5) A点为射击位枪口位置,B点为末端挡弹墙位置,为方便计算,设AB间的距离为100 m;
6) 通过弹道射线分析,保证从A点射出的子弹被防弹构件阻挡,则A、顶棚末端与第1道挡弹梁顶部在一条直线上,A、第1道挡弹梁底部与第2道挡弹梁顶部在一条直线上,…… 以及A、最后1道挡弹梁底部与挡墙顶部在一条直线上;
7) 射击场两侧挡弹墙原有高度为2.2 m;
8) 射击场设有12个射击位,总宽度为25 m。
3.2 数学模型
根据以上模型,将H、h设为两个自变量,当n一定时,利用相似三角形的几何关系,求出各参数与H、h关系。具体计算公式为:
dn=(H-2.2)×100/H
(1)
(2)
(3)
(4)
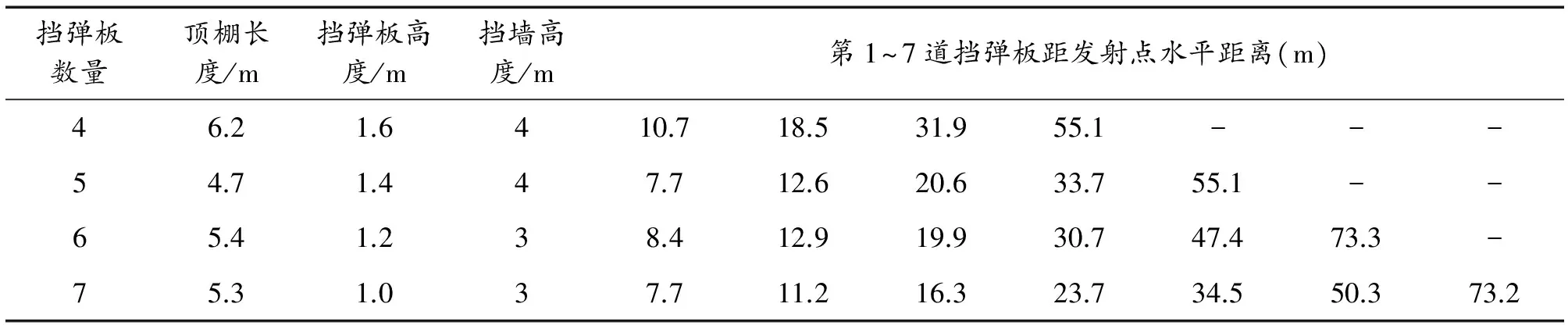
式中:h为挡弹梁的高度;n为射道区挡弹梁数量;di为第i+1道挡弹梁与第i道挡弹梁水平距离(i 基于模型分析,射击场改造内容主要包括新建顶棚、挡弹梁部分和增建挡弹墙部分。射击场的最优化改造就是让这两部分的所需的建筑材料尽可能少,所以通过控制改造防弹面积来达到目的。S为安全防护改造的防弹面积的总和,则有: (5) 挡弹梁段数n取整数,为方便计算分析,将自变量末端挡弹墙高度H取3~10 m范围内整数。将上述5个公式代入到Matlab进行计算(见图8),运行后可以得到n取不同值时S随H、h变化的曲面变化图(见图9),分析S对应的最小值。并且将H取不同值时S对应的最小值进行汇总(见表1)。通过分析比较表1数据,找出射击场改造最优化方案。 图8 n=5时Matlab运行计算截图 3m4m5m6m7m8m9m10m1957.6810.3760.7760.0787.4832.4889.1954.22680.1611.4608.2638.2687.0747.8816.9891.23556.7522.8540.2583.2642.0709.4783.9862.74489.0473.6502.9552.7616.6688.2765.1846.65446.5443.6478.4533.7601.4674.4753.3836.56417.4423.1462.3520.3590.2666.0745.3828.87397.4406.8452.5511.2581.0658.4740.8825.88382.5396.3441.1504.2577.9654.5735.1819.6 图9 n取不同值时,S与H、h之间关系 3m4m5m6m7m8m9m10m14.44.24.03.83.63.43.23.023.02.82.62.42.42.22.02.032.22.02.01.81.81.61.61.441.81.61.61.41.41.21.21.251.41.41.21.21.01.01.01.061.21.21.01.01.00.80.80.871.01.01.00.80.80.80.80.681.00.80.80.80.80.60.60.6 从图9可知,当n≤5时,S存在最小值;当n>5时,S随H、h的增加而增加。 表1可知,其中粗体数字为n取不同值时S的最优解,最优解S随n的增大而减少,所以挡弹梁越多,挡弹面积越小。,n取1时S的最优解是n取8时的近两倍,所以对S的最优值的分析研究可以起到节省材料的作用。当挡弹梁n为1道或2道时,其高度h大于2 m,挡弹梁相对不够稳定,而且其最小面积S相对较大,所以1、2道挡弹梁并不实用;当n=3时,其顶棚长度接近8 m,这将会造成光线不足,所以3道挡弹梁也不实用;n=8时,通过计算可得,y=1.7,d1=2.4,d3=3.5,这3个数据分别为第1道梁距顶棚边缘距离第1、2道梁之间距离和第2、3道梁之间距离,梁顶端距地面3.2 m,宽度25 m但是梁之间小于3.5 m,过于密集,所以挡弹梁段数超过8组也不实用。通过分析,得出n取4~7时4种方案。 将4种方案H、h值代入公式,计算挡弹梁位置,得表3。可以发现n为4、5时,最后一道挡弹墙距射击位距离接近50 m。如果这段距离为50 m,可以起到对50 m靶区遮挡风雨功能,所以对这两种方案进一步优化(见表4)。 优化后的4种方案有各自的优点:4、5段挡弹梁的方案,内部空间较简洁,50 m靶区上方有提供遮挡风雨的建筑构件;6、7段挡弹梁的方案,改建后建筑高度整体较低,两边挡弹墙的改建比较节省材料。 表3 4种方案中各参数值 表4 4种方案优化后各参数值 本文通过弹道射线分析,建立安全防护改造模型,并运用Matlab计算分析,在确保安全性和实用性的前提下,得出射击场安全防护改造的4种优化方案。这4种方案确保射击场的安全,实弹射击训练不会对周围造成威胁,达到节省建筑材料的目的。部队进行射击场改建时,可以参考这4种方案中的数据,达到使用最少建筑材料构建安全的射击场。 [1] DB11/T 1230—2015,射击场设置与安全要求[S]. [2] GB 19079.8—2013,体育场所开放条件与技术要求 第8部分:设计场所[S]. [3] 马莉.MATLAB数学实验与建模[M].北京:清华大学出版社,2010. [4] 洪铁城.领导干部体育设施知识读本 [M].北京:中国建筑工业出版社,2002:153-156. [5] JOHN R H,JR FAIA.Architetural graphic standards[M].大连:大连理工大学出版社,2003:794. [6] 郑涛.基于GIS的营区室外射击场安全设计方法探析[J].自动化与仪器仪表,2016(5):60-63. [7] 李小蓉,缪剑峰,紫怡.驻城市部队营区训练场规划探析[J].后勤工程学院学报,2015(1):24-27,33. [8] HENDRIK B.伦敦奥运会射击馆[J].城市建筑,2012(11):62-67. [9] 庄惟敏,祁斌.2008 奥运会北京射击馆建筑设计[J].建筑学报,2007(10):38-45.
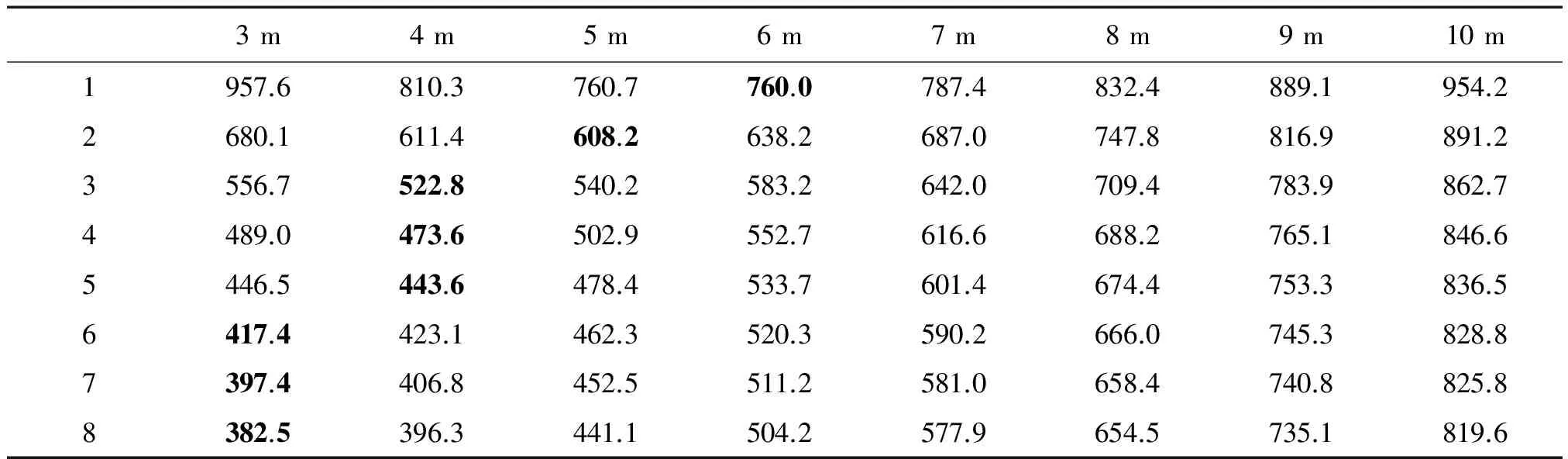


3.3 结果分析

4 结论
