用穷举法解爱因斯坦问题
2018-02-28李振夏
李振夏
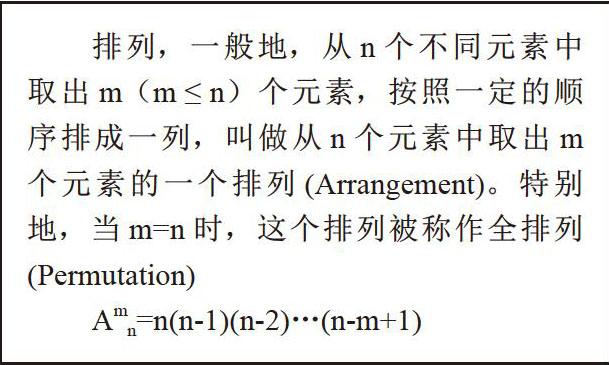

摘要 上个世纪,大科学家爱因斯坦提出了一道非常经典的逻辑题“谁在养鱼”?这是一道很非常经典的智力题,据爱因斯坦说,全世界只有大约2%的聪明人,能够推得出这个问题的答案。在没有计算机的年代,相信普通人看到这个问题无从下手,聪明者基本都是以表格的方式来推导。计算机出现后很多依靠人脑无法完成的事情可以变得顺利成章了。本文要介绍的方法就是这样:以穷举法来破解这道题。
【关键词】爱因斯坦 穷举法 Java编程 排列组合 长郡中学
1 问题描述
上个世纪,大科学家爱因斯坦提出了一道非常经典的逻辑题,题目的内容是这样的:在一条街上有五个不同颜色的房间排成一排,每个房间里分别住着一个不同国籍的人,每个人都喝一种特定品牌的饮料,抽一种特定品牌的烟,养一种宠物,没有任意两个人抽相同品牌的香烟,或喝相同品牌的饮料,或养相同的宠物,又知:
(1)英国人住在红房子里。
(2)瑞典人养狗。
(3)丹麦人喝茶。
(4)绿房子紧挨着白房子,在白房子的左边。
(5)绿房子的主人喝咖啡。
(6)抽PALL MALL牌香烟的人养鸟。
(7)黄房子里的人抽DUNHILL牌的烟。
(8)住中间房子的人喝牛奶。
(9)挪威人住在第一个房子里(最左边)。
(10)抽BLENDS香煙的人和养猫的人相邻。
(11)养马的人和抽DUNHILL牌香烟的人相邻。
(12)抽BLUEMASTER牌香烟的人喝啤酒。
(13)德国人抽PRINCE牌香烟。
(14)挪威人和住蓝房子的人相邻。
(15)抽BLENDS牌香烟和喝矿泉水的人相邻。
问题:谁在养鱼?
2 解题思路
就这道题来说,穷举法是最直接也是容易让人理解的方法。所谓穷举法的基本思想是根据题目的部分条件确定答案的大致范围,并在此范围内对所有可能的情况逐一验证,直到全部情况验证完毕。若某个情况验证符合题目的全部条件,则为本问题的一个解;若全部情况验证后都不符合题目的全部条件,则本题无解。就本道题而言肯定就只有一个答案。
在正式计算之前,需要先来讨论一下答案的形式和范围。就这套题而言,有五个房子(在面向对象的程序中称为实体),每个房子从左到右依次排列,每个房子有个序号分别从O到4(在这里就按照程序的思维来进行,从O开始进行编号),每个房子分别有五个属性:房屋的颜色(以下简称颜色)、居住者的国籍(以下简称国籍)、居住者的喜爱的饮料(以下简称饮料)、居住者喜欢的香烟(以下简称香烟)、居住者养的宠物(以下简称宠物)。这五个属性每种属性有5个值,那么一共有多少个可能的解呢?为了弄清这个问题,让我们先从一个属性来分析,假设单单就颜色来说,总共5中颜色,分给5套房子,有多少中可能性呢?在学了数学的排列定理后,我们知道这里其实就是一个排列组合问题:
就颜色的来说,实际上就是5的全排列。可能的组合数为:5*4*3*2*1=120种排列方式。知道了就一种属性来说有120种可能性,那么就5个属性来说,他们的可能组合数为120*120*120*120*120= 24883200000个可能的解(这么庞大的数字,如果不做优化就人来说几乎就是不可能完成的)。
了解了解题思路后,接下来要做的就是分别对颜色、国籍、饮料、香烟和宠物计算出每个属性的所有可能的排列组合并将这些组合放到5个数组里面,然后再用多层循环的方式,从每个数组中取出一个组合进行校验:其实简单,具体如何校验呢?题中的15调线索,每条就是一个校验规则。
3 解题算法
3.1 数据初始化
声明5各列表,每个列表中依次放入相关的选项
private static List nationalities;
private static List houseColors;
private static List drinks;
private sratic List smokings;
private sratic List pets;
static{
//初始化数据
nationalities= Arrays.asList(“英国”,“瑞典”,“丹麦”,“挪威”,“德国”);
houseColors= Arrays.asList(“红”,“绿”,“白”,“黄”,“蓝”);
drinks= Arrays.asList(“茶”,“咖啡”,“牛奶”,“啤酒”,“矿泉水”);
smokings= Arrays.asList("PALLMALL", "DUNHILL", "BLENDS",”BLUEMASTER", "PRINCE");
pets= Arrays.asList(“狗”,“鸟”,“马”,“猫”,“鱼”);
)
3.2 排列组合的计算
就本题而言,一个最为核心和重要的就是如何算出一组数据的排列组合。设a、b、c、d、e五个数为一组,如何算出这5个组的所有排列组合的形式。根据假设对一个有n位的数组来说,第一位有n种选择,第2位有n.1种选择,第一位和第二位的组合有n*(n-l)各,他们与3位的组合有n*(n-1)*(n-2)个。依次进行递归前面n-l位与最后一位的组合只剩下一种形式,依次得出算法如下:
/{{
*求list中元素的所有排列组合
* @param list列表中的元素
* @return
*/
public static List list){
List
List line=newArrayList();
permutarion(line, lisr, result);
return result,
)
/**
*计算所有的排列组合
* @param line前面元素的组合
* @param remains剩余还没有组合的元素
* @param result保存最终的计算结果,里面的每个list是一种组合形式
*/
private static void permutation(Listline, List remains, List
line= cloneList(line);
remains= cloneList(remains);
int size= remains.size(),
if (size==1){∥如果只有一个元素,那么就只有直接用前面的组合跟这个元素进行拼合
line.add(remains.get(0》;
result.add(line);
return,
)
for (inti=0;i
String one= remains.get(i);//取出某一個元素
Lisr remains2=without(remains, one);//剔除该元素的列表
permutation(one, cloneList(line),remains2, result);
)
)
*计算出某一个元素与前面组合的拼合结果
* @param one某个元素(下一个加入的元素)
* @param line需要加入的队列(某个组合)
* @param remains2剩余的元素
* @param result存储最终的结果
*/,
private static void permutation(Stringone, List Iine, List remains2,List
line= cloneList(line);
line.add(one);
permutation(line, remains2, result);
)
3.3 规则检验
有了上一小节的排列算法,我们可以每次先对房屋(或房屋主人的)国籍、颜色、饮料、香烟、宠物算出所有的排列组合,然后循环这些组合,每次针对这五个属性各拿出一个组合进行校验。题中的15条线索就是15个校验规则,我们需要针对每个规则完成一个检查方法,某一组合符合所有的规则,那么就是正解。以第一个规则为例方法如下:
*检查条件:英国人住在红房子里。
* @param nationList国籍列表
* @param colorList房屋颜色
* @retum检查通过返回true,否则返回false
private static boolean checkEnglishInRedHouse(List nationList, ListcolorList){
int index= nationList.indexOf(“英国”);∥获得英国人做在的房屋序号
String color= colorList.get(index);//获得同一序号的房屋颜色
retum红”equals(color);
)
3.4 穷举算法
在以上的算法的基础,最终的穷举算法如下:
public static void main(String[] args){
List
List
List
List
List
index=O:
long beginTime=System.currentTimeMillis();
int size= nationPermutations.size();//
//以下针对每个属性循环,检验每个解
for (intn=O;n
List nationList=nationPermutations.get(n);
for (int c=O;c
List colorLisr=colorPermutations.get(c);
for (int d=O;d
List drinkList=drinkPermutations.get(d);
for (inr s=O;s
List smokeList=smokePermutations.get(s);
for (intp=0;p
Lisr petList=petPermutations.get(p);
index++;
if (checkPass(narionLisr,colorList, drinkList, smokeList, petList》{
//检验通过
System.out.println("计算用时:”+ (System.currentTimeMillis() -beginTime)+“毫秒”);
printResult(nationList,colorList, drinkList, smokeList, petList);
retum,
) else{
//System.outprintln("error at”+index);
)
}
}
)
)
)
System.out.println(”程序运行结束!”);
)
3.5 算法优化
在上一小节中,依次用了5层循环来对检验每个解,前面说过这样的解一共有24883200000个。这样的数量对于计算机来说运算次数也还是非常大的。为了最大幅度的减少运算次数,可以在外层循环中就逐步加入一些校验规则,筛选掉一些无用的解。大致如下:
for (intn=0;n
List nationLisr=nationPermutations.get(n);
if(! checkFirstHouseIsNorwegian(nationList》{//检查第一间房是否是挪威人,这个只跟nationList有关系
continue,
}
for (int c=0;c
Lisr colorList=colorPermutations.get(c);
if (!checkGreenLeftOfWhite(colorList》{∥检查绿色房子是否在白色房子的左边
contmue,
}
if( !checkEnglishInRedHouse(nationList, colorList》{//检查英国人是否住红色房子
contmue,
}
if(! checkNearbyNorwegianWirhBlueHouse(nationList, colorList》{∥挪威人和住藍房子的人相邻
contmue,
)
for (int d = 0;d
)
)
)
提前加入校验的原则就是,在某一层循环加入的校验算法只与前面几层的属性相关,这样校验方法才能正常执行。
3.6 计算结果
4 总结
采用穷举法来解题的最直接的优点就是直观、便于理解。从缺点方面来说,穷举法最大的缺点就是通常计算量都很大,但本处解题由于对程序进行了优化,提早加入校验方法,已经让计算量大幅的降低,运算效率大大提高。(程序查看和下载地址:https://giteecom/lizhenxia/einstein).
参考文献
[1]张传鹏.高考数学进阶特训[M]。浙江:浙江大学出版社,2016.
[2]白喜琇(韩).狄利克雷教你学选择和排列[M].安徽:黄山书社出版,2016.
[3]明日科技.Java从入门到精通(第4版)[M].北京:清华大学出版社,2016.
[4]宋娟.Java常用算法手册(第3版)[M].北京:中国铁道出版社,2016.
[5] Robert Sedgewick(美),KevlnWayne(美)著;谢路云译,算法第4版Algorithms Fourth Edition[M].北京:人民邮电出版社,2012.
