整数最优规划在收入模型中的应用

□卫奕冰 张 喆

（延边大学理学院数学系 吉林 延吉 133000）

A、B、C、D 4 人需要完成甲、乙、丙、丁 4 种软件的开发，这4个项目的收入费用分别为1 000元、2 000元、3 000元、4 000元，分别安排 A、B、C、D 4人完成每个软件不同阶段的项目任务。完成甲项目，A需要用3 d，B需要用4 d，C需要用 2 d，D需要用3 d；完成乙项目，A需要用5 d，B需要用6 d，C需要用4 d，D需要用2 d；完成丙项目，A需要用5 d，B需要用6 d，C需要用7 d，D需要用4 d；完成丁项目，A需要用6 d，B需要用7 d，C需要用10 d，D需要用8 d。现在要对这4名软件开发人员和4个项目进行安排，使该公司实现1 a(365 d）内的收入最大化。要完成以上任务，需要考虑两方面因素。一方面，需要考虑完成一个项目总的时间和，以便将时间控制在规定的范围内。另一方面，这是一个收入最大化的问题，需要基于最优规划，建立合理的计算模型[1]。

1 多元最优规划模型的建立

基于项目数量，建立收入的目标函数，即W=1 000x1+2 000x2+3 000x3+4 000x4

在上述公式中，W代表一年的收入，决策变量x1、x2、x3、x4分别代表 1 a内所完成的甲、乙、丙、丁 4 个项目的工作量[2]。由于完成项目的天数有所限制，所以得到线性回归方程组：

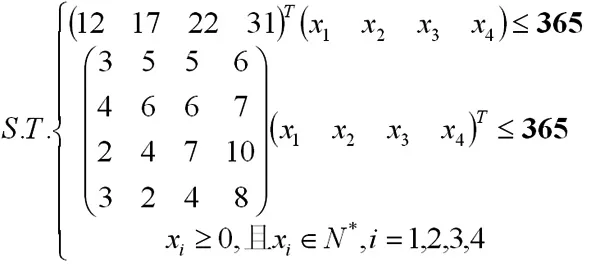
2 多元最优规划模型求解

在处理多元线性回归方程组的过程中，由于最优规划模型与概率模型具有一定的联系，所以可以采取随机模拟的方法——蒙特卡罗法进行求解[3]。通过生成一定量的随机数，利用MATLAB进行统计模拟与抽样，从而获得问题的最优近似解。MATLAB蒙特卡罗法算法步骤如下[4]。

（1） 生成的 x1、x2、x3、x4分别位于 [0，30]、[0，20]、[0，16]、[0，11]的随机数[5]。

（2）对生成的随机数进行取整。

（3）利用枚举法的思想，对产生的随机数进行约束条件的迭代限制。

（4）不断循环运算，最终得到最优解[6]。

经过多次运算后，得到了最优解，即①x1=18，x2=20，x3=16，x4=11。②x1=16，x2=21，x3=16，x4=11。

3 结果分析

通过利用蒙特卡罗法进行多次随机模拟之后，得到最终结果：W=150 000

此时，出现了两种工作安排方案。①甲、乙、丙、丁项目分别为 18、20、16、11。②甲、乙、丙、丁项目分别为16、21、16、11。利用Lingo对该最优规划问题进行进一步的检验计算，得到与蒙特卡罗方法相同的结果，由此可以判断，蒙特卡罗方法具有可靠性。

4 结束语

通过分析，可以通过建立合理的目标函数与约束条件，利用蒙特卡罗方法求得整数解，实现收入最大化的目标，为企业创造更多的利润。