人工气候环境下考虑荷载应力影响的混凝土温度响应研究

蒋建华，胡飞飞，秦亚俊

(河海大学 土木与交通学院，江苏 南京 210098)

0引 言

温度是影响混凝土结构耐久性的重要因素之一，而混凝土结构由于自重等原因是带荷载工作的，荷载的存在会在混凝土内部产生应力。为了贴合实际，研究混凝土温度响应时应考虑荷载应力的影响。因此，研究荷载应力对混凝土内部温度响应的影响有一定的工程和理论价值。

目前很多学者作了关于混凝土内部温度响应的研究。蒋建华等[1-2]通过对混凝土内部温度响应规律的研究，发现混凝土内部温度与环境温度有一定的滞后性，并建立了混凝土内部温度响应预测模型。刘鹏等[3-4]研究了混凝土内部微环境温度响应，建立并验证了温度作用谱模型。鲁彩凤等[5]研究了粉煤灰掺量对混凝土内部温度响应的影响。Min等[6]研究了不同损伤水平混凝土的温度响应。混凝土的导热系数是混凝土温度响应过程中的重要参数。肖建庄等[7]研究了水灰比、温度、干湿状态等因素对混凝土导热系数的影响。Zhang等[8]研究了混凝土损坏程度对导热系数的影响。陈春等[9]建立了基于最小热阻理论的混凝土导热系数计算模型。从以上研究可以看出，目前关于混凝土内部温度响应的研究主要集中在内外环境的相互影响方面，而对荷载作用下混凝土温度响应方面的研究较少。

本文通过人工气候环境下混凝土温度响应试验，研究了不同应力水平对混凝土内部温度响应的影响，并且比较了拉/压应力条件下混凝土内部温度响应规律，基于理论分析和试验结果，建立了考虑荷载应力影响的混凝土导热系数计算模型。本文的研究成果可以为实际混凝土结构的内部温度响应预测奠定一定的理论基础。

1试验方案

1.1试件设计

试验采用3种强度混凝土试件，配合比如表1所示，试验中水泥采用P.O42.5普通硅酸盐水泥，细骨料采用河砂(中砂)，粗骨料采用粒径5～15 mm的碎石，拌合水采用普通自来水。

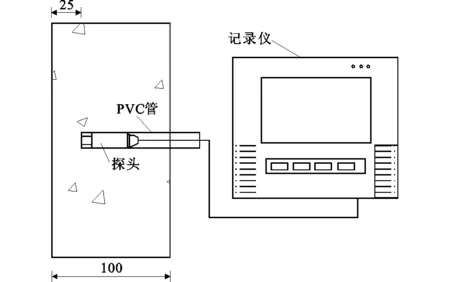
试件尺寸为100 mm×100 mm×200 mm，采用预埋PVC管的方式为温湿度探头预留测量空间，PVC管预埋在混凝土试件的中心位置，如图1所示。

本文分别研究了拉/压应力水平为0%(无应力水平)，20%，40%的混凝土内部温度响应情况，每种应力水平浇筑5个试件，其中2个用于温度响应试验，3个用于强度试验。定义应力水平为φ，其值为加载应力与混凝土试件抗压强度或抗拉强度的比值。

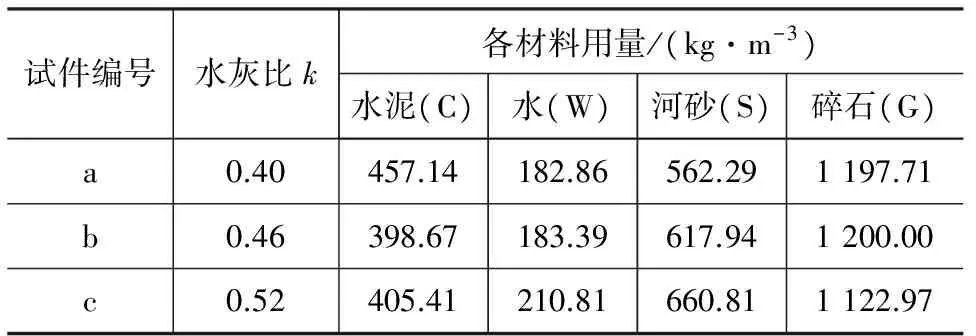
表1混凝土配合比Tab.1Mix Proportion of Concrete

1.2试验装置

为了保证试验环境的稳定性，在人工气候试验箱中进行试验，通过温湿度传感器记录混凝土试件内部温度，实现温度数据的自动采集、存储，如图1所示。

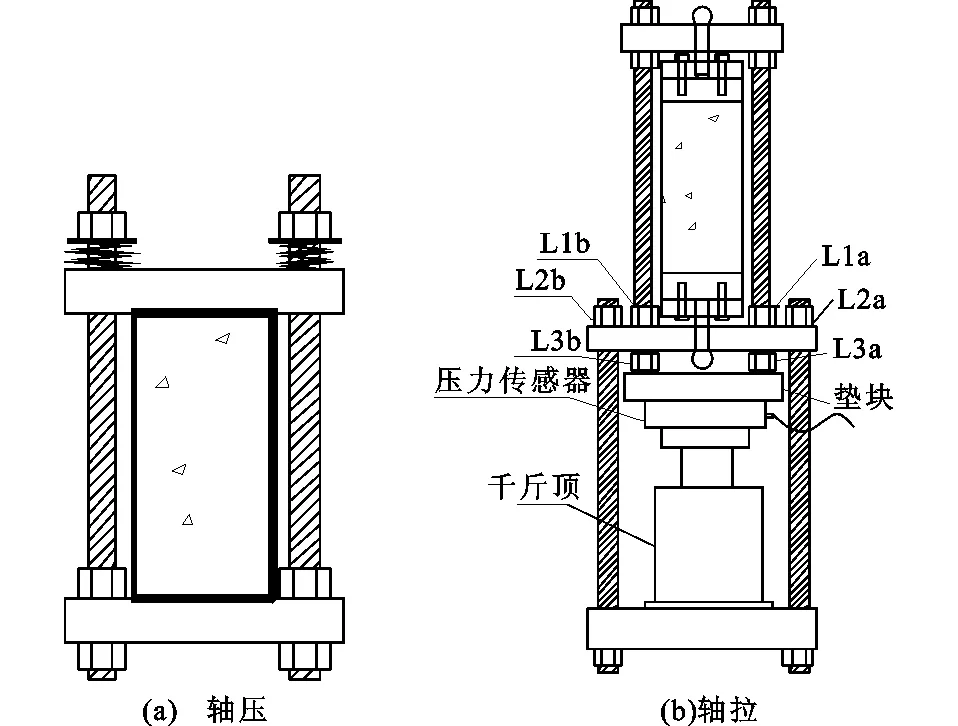
为了实现持续荷载应力对混凝土试件的作用，采用自制持续加载装置对混凝土试件施加应力，装置的设计如图2所示。为了尽可能消除应力分布不均匀的影响，本文采用轴压和轴拉的加载方式分别来模拟压应力和拉应力的作用。

1.3试验过程及方法

1.3.1混凝土试件拉、压强度的确定

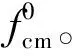
1.3.2压应力的施加

为减小混凝土内部湿度差异对其温度响应的影响，将养护好的混凝土试件放入烘箱使其内部湿度达到60%±2%，在混凝土侧面粘贴混凝土应变片，压力传感器和应变片都与应变仪相连，通过千斤顶施加压力，通过应变仪的应变来控制应力损失。

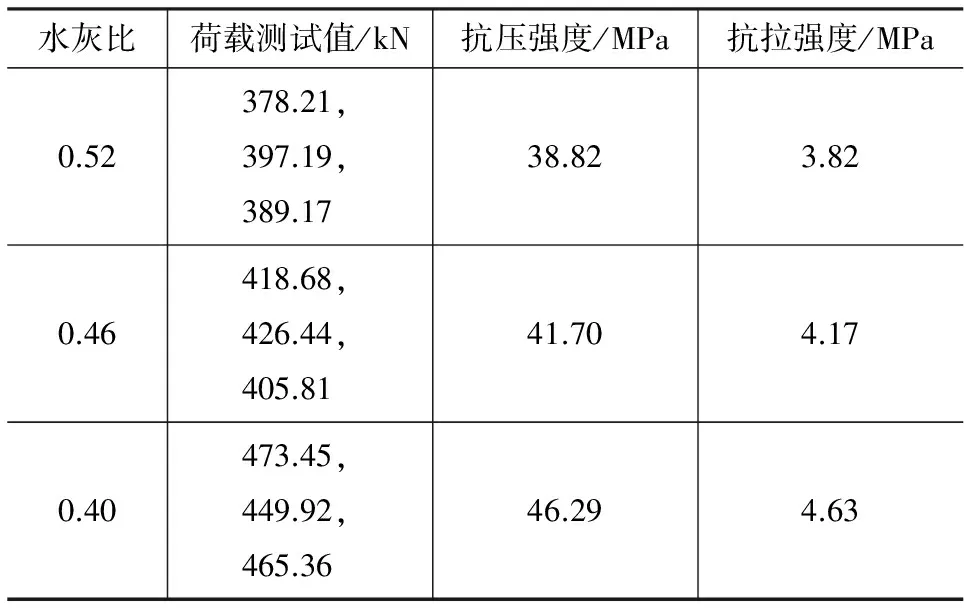
表2混凝土抗压、抗拉强度Tab.2Compression and Tensile Strengths of Concrete

1.3.3拉应力的施加

取出达到初始湿度要求的试件，用砂轮磨平试件端面，利用黏钢胶将制作的钢板粘贴于试件两端。为了保证黏钢胶的有效厚度，在其中放置1圈扎丝。拉应力的施加与压应力大致相同，区别在于拉应力施加装置的下半部分为临时加载装置。

2试验结果与分析

试验箱温度设为35 ℃,湿度为60%±2%，时间间隔10 min采集温度数据。由于相同水灰比的混凝土在应力作用下温度响应曲线十分接近，为获得“放大”效果,温度数据只取了前150 min。

2.1压应力条件下混凝土温度响应规律

混凝土在压应力作用下的温度响应过程如图3所示，不同水灰比混凝土在不同压应力下的温度响应过程相似，均属于非线性的热力学瞬态过程。混凝土内部温度响应前期较快，然后逐渐趋于平缓。

由图3可知，相同水灰比的混凝土，压应力越大，其温度响应速率越快，这是由于压应力的存在使混凝土产生压缩形变，压缩内部孔隙，从整体上强化了由固态物质为主导的热量传递通道，压应力水平越高，这种强化作用越明显。以水灰比为0.40的混凝土试件温度响应为例，从计算试验开始到温度上升5 ℃所需的时间可以发现，无应力水平、20%压应力水平与40%压应力水平作用下所需的时间分别为38.3，31.8，27.5 min。

2.2拉应力条件下混凝土温度响应规律

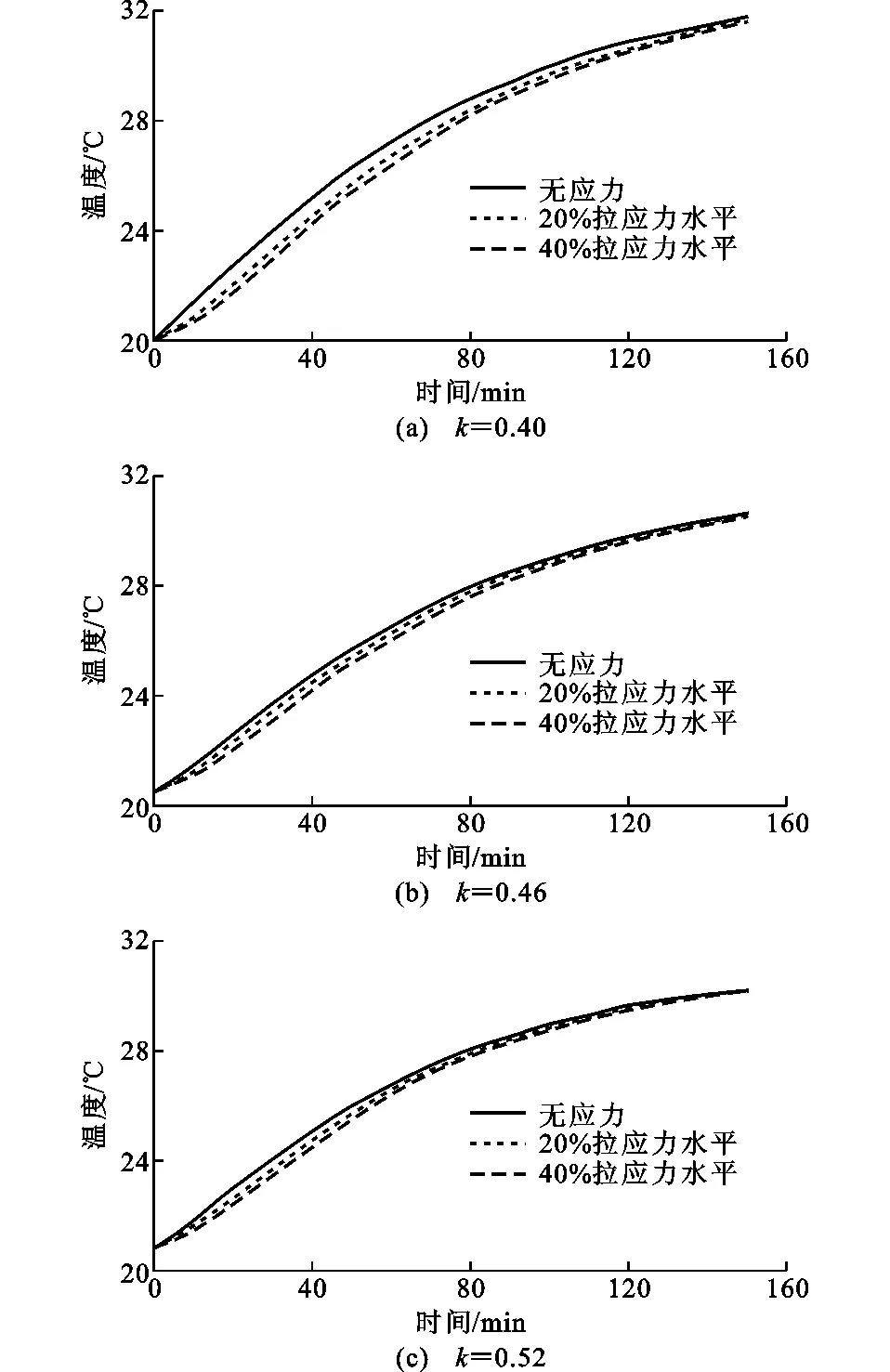
拉应力作用下的混凝土温度响应过程如图4所示。相同水灰比的混凝土，拉应力越大，其温度响应速率越慢，拉应力的存在使混凝土产生拉伸形变，从整体上削弱了由固态物质为主导的热量传递通道，拉应力水平越高，这种弱化作用越明显。以水灰比为0.40的混凝土试件在拉应力作用下的温度响应过程为例，计算混凝土从试验开始到温度上升5 ℃所需的时间，计算结果表明，无应力状态、20%拉应力水平、40%拉应力水平作用下所需的时间分别为38.3，44.2，46.7 min。

2.3拉应力与压应力下温度响应结果的比较

从前文给出的不同水灰比混凝土在不同应力(拉/压应力)条件下的温度响应结果可以发现：在水灰比相同时，压应力条件下混凝土内部温度响应比无应力时快；拉应力条件下混凝土内部温度响应比无应力时慢。为更直观地比较拉、压应力对混凝土内部温度响应造成的差异，取不同水灰比混凝土在不同应力条件下的响应结果，如图5所示。

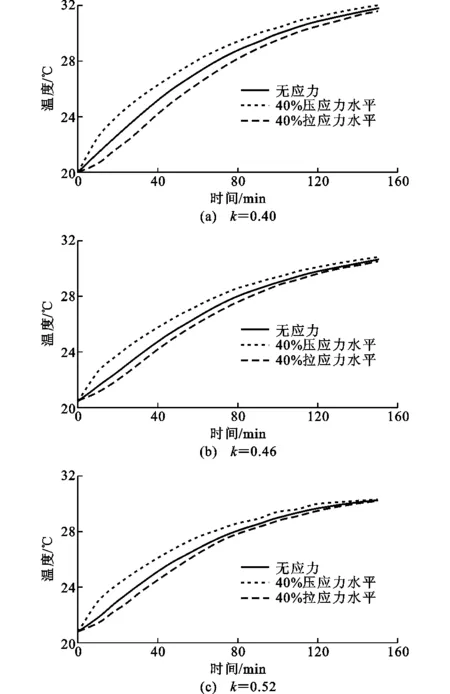
由图5可见，同一水灰比时，压应力条件下的温度响应速率比拉应力条件下快。以水灰比为0.40的混凝土试件温度响应过程为例，40%拉应力、无应力、40%压应力条件下试验从开始到温度上升5 ℃所需的时间分别为46.7，38.3，27.5 min。

另外，各组试验结果中，以相同时间点的无应力条件下混凝土内部温度响应结果为参照，40%压应力条件下的温度响应结果与参考结果之间的差值比40%拉应力条件下的差值要大。这表明相同水平的压应力比拉应力对混凝土温度响应的影响更明显，这是由于混凝土的极限压应变大于其极限拉应变，对于同样的应力水平，压应力会使混凝土产生更大的应变，从而会压缩更多混凝土内的孔隙通道，使固态物质占的比例更大。

3考虑荷载应力影响的混凝土导热系数计算模型

3.1导热系数计算理论

试验过程中，同一组试验中的外部环境是一致的，因此可以将热源视为一致的。由传热学基本原理可知，半无限大均质物体在常热流密度作用下，非稳态导热过程的微分方程为[8]

(1)

定解条件为

式中：t为温度响应时间；q为热流密度；qw为表面热流密度；a为材料的导温系数(热扩散率)；x为混凝土试件内深度。

利用定解条件对公式(1)求解

(2)

根据傅里叶定律，式(2)可进一步改写为

(3)

其中：θ为过余温度，θ=T(x,t)-T0，T0为半无限大均质物体的初始温度，T(x,t)为距离混凝土表面距离为x的位置在t时刻的温度；λ为材料的导热系数。

分离变量并对式(3)积分，同时有x→+∞时，θ=0，即

(4)

于是，常热流密度条件下半无限大均质物体内部温度分布的表达式为

(5)

式中：ierfc(·)为高斯误差补函数的一次积分。

公式(5)给出了测定混凝土热扩散率的恒定作用热源法的理论依据。若已知混凝土试件t=0时刻的初始温度为T0，试件表面在恒定平面热源qw作用下，经过t时刻，同时测定试件表面温度T|x=0和距离表面δ处的试件内部温度T|x=δ。将上述参数代入公式(5)可得

(6)

又已知ierfc(0)=0.564 2，由公式(6)得

(7)

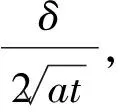
3.2计算结果

以水灰比为0.40的试件在无应力作用下的温度响应曲线为例，试件开始时刻的温度为20 ℃，记为T0，当过程进行到t=60 min时，混凝土内δ=25 mm深度处的温度上升为T|x=δ=27.2 ℃，此时设混凝土试件的外表面已经达到试验设定的目标温度，也即T|x=0=33.5 ℃，将T0，T|x=δ与Tx=0代入式(7)得

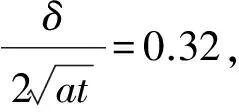
表3混凝土在应力条件下的导温系数Tab.3Temperature Diffusivity of Concrete Under Stress

导温系数a=λ/(ρc)，为了简化，忽略应力对混凝土试件密度ρ和比热容c的影响。因此，混凝土导温系数之间的关系可以等效为导热系数λ的关系，若将各组试验中无应力状态下的混凝土导热系数设为1，则可以确定混凝土有应力与无应力状态下导热系数的数量关系(图6)。

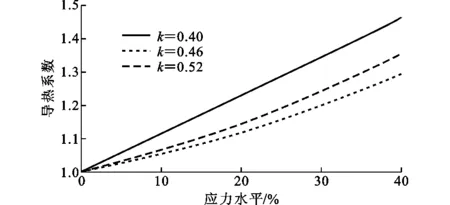
由图6可以看出，不同水灰比的混凝土试件其导热系数随着压应力的增大而不断增加。不同水灰比的混凝土试件随着压应力水平的增加其导热系数的增长幅度不同，这是因为不同水灰比的混凝土在受相同水平的压应力作用时，其内部密实度变化幅度不同。因此，在进行分析时，应该考虑水灰比这一变量。

将混凝土试件在不同压应力条件下的导热系数λc与无应力状态下的导热系数λ0的比值定义为压应力影响系数Kλ，通过对表3的数据进行回归分析，得到不同压应力条件下Kλ的预计公式

0%≤φc≤40%

(8)

式中：φc为压应力水平，是混凝土受到的压力与混凝土抗压强度的比值。

同样地，也可由表3得到混凝土在不同拉应力水平下导热系数的变化趋势，具体见图7。

由图7可见，不同水灰比的混凝土试件随着拉应力的增大其导热系数减小，并且导热系数相对于无应力状态下的导热系数减小幅度不同。这是由于混凝土受同样的拉应力作用时，其内部密实度变化幅度不同。因此，在进行分析时也应该考虑水灰比这一变量。

将混凝土试件在不同拉应力条件下的导热系数λt与无应力状态下的导热系数λ0的比值定义为拉应力影响系数Kλ，通过对表3的数据进行回归分析，得到不同拉应力条件下Kλ的预计公式

0%≤φt≤40%

(9)

式中：φt为拉应力水平，是混凝土受到的拉应力与混凝土抗拉强度的比值。

文献[11]中提出的不同水灰比混凝土在不同含湿状态下的导热系数预计模型为

λ=1.893-1.223k+0.766 3S

(10)

式中：S为混凝土孔隙水饱和度。

结合式(8),(9)与式(10)，便可以得到不同水灰比混凝土在压应力和拉应力水平下的导热系数预计模型，如公式(11)所示

(11)

4结语

(1)在水灰比相同的情况下，混凝土压应力水平越高，其温度响应速率越快，而拉应力水平越高，其温度响应速率越慢。

(2)对于同样的应力水平，压应力对混凝土温度响应的影响效果更显著。

(3)混凝土的导热系数随着压应力水平的增加而增加，拉应力水平下与其相反；提出了一种计算混凝土导热系数的方法，并建立了不同应力水平下混凝土导热系数预计模型。

(4)为了完善应力对混凝土温度响应的影响研究，关于应力对混凝土密度和比热容的影响有待进一步探究。

[1] 蒋建华,袁迎曙,张习美.自然气候环境的温度作用谱和混凝土内温度响应预计[J].中南大学学报:自然科学版,2010,41(5):1923-1930.

JIANG Jian-hua,YUAN Ying-shu,ZHANG Xi-mei.Action Spectrum of Temperature in Natural Climate Environment and Prediction of Temperature Response in Concrete[J].Journal of Central South University:Science and Technology,2010,41(5):1923-1930.

[2] 蒋建华,袁迎曙,孙红萍,等.人工气候下混凝土温度响应规律与预计模型[J].中国矿业大学学报,2009,38(6):800-805.

JIANG Jian-hua,YUAN Ying-shu,SUN Hong-ping,et al.Response Laws and Prediction Model of Temperature Change in Concrete in a Controlled Climate[J].Journal of China University of Mining and Technology,2009,38(6):800-805.

[3] 刘 鹏,余志武,宋 力,等.自然环境中混凝土内微环境温度响应[J].湖南大学学报:自然科学版,2014,41(9):60-65,71.

LIU Peng,YU Zhi-wu,SONG Li,et al.Response of Micro Environmental Temperature in Concrete Under the Natural Environment[J].Journal of Hunan University:Natural Science,2014,41(9):60-65,71.

[4] 刘 鹏,余志武,宋 力.自然环境温度作用谱和混凝土温度响应谱[J].建筑材料学报,2014,17(3):532-537,547.

LIU Peng,YU Zhi-wu,SONG Li.Spectra of Temperature Action and Response of Concrete in Natural Environment[J].Journal of Building Materials,2014,17(3):532-537,547.

[5] 鲁彩凤,袁迎曙.人工气候环境下粉煤灰混凝土微环境温度响应预计[J].中国矿业大学学报,2012,41(4):571-577,612.

LU Cai-feng,YUAN Ying-shu.Microenvironment Temperature Response Prediction for Fly Ash Concrete in Artificial Climate Environment[J].Journal of China University of Mining and Technology,2012,41(4):571-577,612.

[6] MIN H G,ZHANG W P,GU X L.Experimental Study on Temperature Response in Damaged Concrete Under Atmospheric Environment[J].Key Engineering Materials,2016,711:404-411.

[7] 肖建庄,宋志文,张 枫.混凝土导热系数试验与分析[J].建筑材料学报,2010,13(1):17-21.

XIAO Jian-zhuang,SONG Zhi-wen,ZHANG Feng.An Experimental Study on Thermal Conductivity of Concrete[J].Journal of Building Materials,2010,13(1):17-21.

[8] ZHANG W P,MIN H G,GU X L.Temperature Response and Moisture Transport in Damaged Concrete Under an Atmospheric Environment[J].Construction and Building Materials,2016,123:290-299.

[9] 陈 春,钱春香,许燕波.基于最小热阻理论的混凝土导热系数计算模型[J].东南大学学报:自然科学版,2012,42(2):383-387.

CHEN Chun,QIAN Chun-xiang,XU Yan-bo.Calculation Model for Thermal Conductivity of Concrete Based on Minimum Thermal Resistance Theory[J].Journal of Southeast University:Natural Science Edition,2012,42(2):383-387.

[10] 章熙民,任泽霈,梅飞鸣.传热学[M].5版.北京:中国建筑工业出版社,2007.

ZHANG Xi-min,REN Ze-pei,MEI Fei-ming.Heat Transfer[M].5th ed.Beijing:China Architecture & Building Press,2007.

[11] 蒋建华.气候环境作用定量模式及其在混凝土结构寿命预计中应用[D].徐州:中国矿业大学,2011.

JIANG Jian-hua.Quantitative Model of Climate Load and Its Applications in Life Prediction Concrete Structures[D].Xuzhou:China University of Mining and Technology,2011.