大跨径钢桁梁悬索桥疲劳特性研究
2018-02-28王盼,王莹
王 盼,王 莹
(湖北省城建设计院股份有限公司,湖北 武汉 430051)
0 引言
随着计算机技术的显著进步和桥梁施工工艺的大幅提高,桥梁工程界近年来建立了很多跨越江河的特大型桥梁,桥梁建设事业得到了飞速的发展,尤其是自重很轻的钢桥在很多大型工程中得到了应用。在钢桥中板件连接方式较多[1],其中焊接方式在现代钢桥中应用最广泛,然而,焊接钢桥也带来了严重的疲劳破坏问题。由于现代桥梁结构复杂程度日趋增加,钢结构桥梁中会产生一些规范中未涉及到的构造细节,设计人员无法用传统的方法进行设计和评估钢构件构造细节的疲劳寿命。国内外钢桥由于疲劳破坏而产生事故的案例已数不胜数,早在1967年,美国的Point Pleasant桥[2]在眼杆钉孔的地方有两条疲劳裂纹突然断裂,导致整座桥瞬间垮塌,造成了巨大的经济损失,由此引起了人们对钢桥疲劳问题的关注。同年,国内京包线248#桥[3]上梁体突然崩掉一块长约1.75m、高约0.22m的钢梁,该桥上部结构采用轧制工字钢,疲劳裂纹起始于梁体下部气焊补孔位置,由于气焊孔裂纹的扩展导致了事故的发生。该事故表明补焊会在钢梁上造成新的焊接缺陷,引起周围材质变脆,最终导致桥梁疲劳破坏。目前全焊钢桁梁的加劲梁在斜拉桥上已得到广泛运用,主梁以受压力为主,已取得了成功,但在悬索桥上还没有运用的实例。悬索桥加劲梁主桁杆件既有受拉工况也有受压工况,应力变化幅度大,对钢构件的焊接设计和施工工艺要求都很高。因此,对全焊钢桁梁焊缝交叉部位过焊孔新型关键构造细节进行疲劳分析,在保证桥梁的安全运营上具有重要的理论意义与工程实用价值。
钢结构疲劳的计算理论发展在20世纪40年代以后[4-7]。目前钢结构的疲劳研究中主要取得了一些成果:(1)采用不同的理论算法分析钢结构疲劳特性,得出特定结构构件疲劳计算公式;(2)通过试验获得了钢结构不同构造细节的疲劳特性,并以此制定了上述构造细节规范;(3)在试验的基础上开发出众多数值模拟软件,用于钢结构的疲劳寿命预测。
国内外钢结构疲劳研究理论比较成熟,但是公路钢桥的疲劳评估仍处于起步阶段,尤其是对于跨度、柔度特别大的全焊公路悬索桥,相关的研究还没有涉及[8]。大型钢桁梁悬索桥的主桁杆件采用全焊形式,出现了钢桁梁焊缝交叉部位过焊孔新型关键构造细节,并且各国规范中均未涉及到此种构造细节的疲劳计算方法。目前,获得新型构造细节疲劳设计曲线最可靠的方法是足尺试验,但是由于需要耗费大量的资金,试验次数受到限制,试验结果离散性较大,单次的试验结果代表性不强。因此本研究以某大跨径钢桁梁悬索桥为研究对象,基于名义应力法,运用ANSYS Workbench建立不同构造细节的疲劳分析实体模型,对比分析两种过焊孔构造的细节疲劳性能,确定出适用于大跨径公路悬索桥钢桁梁的构造细节,并验算构造细节的疲劳性能,在此基础上提出相应的疲劳补强措施,确定补强方式,获得补强后构造细节的疲劳性能。
1 工程背景与疲劳分析理论
1.1 工程背景
本研究中某大跨径悬索桥为双层公路钢桁梁悬索桥,主跨跨径为1 700m,两侧边跨的跨径为465m,大桥立面布置如图1所示。主桁由钢材q345qD焊接而成,双层共高10m,单个钢桁梁焊接节段的长度为9m。主桁的上弦杆、下弦杆横截面采用矩形加劲肋截面,弦杆的横向距离为28m,内设置加劲肋,上下弦杆之间的竖向竖杆采用I形截面,斜向腹杆采用矩形加劲肋截面,见图2。

图1 悬索桥立面布置图(m)

图2 主桁杆件结构图(mm)
因为全焊结构可以将各杆件预先在工厂焊接完毕,现场安装时可以大大节省工期,因此本研究中的悬索桥的主桁杆件采用全焊结构。由于主跨跨度大,需分节段焊接,在主桁杆件的焊接过程中,大部分位置会存在盖板对接焊缝与竖板对接焊缝的交叉,相应的部位会出现过焊孔,导致截面削减而引起钢桁梁疲劳问题。
1.2 疲劳分析理论
名义应力法为钢结构疲劳分析中的经典方法。名义应力是不考虑结构自身局部面积削弱的情况下结构有效面积的平均应力[9-10]。如一根实心钢管原面积为A,受到拉力F作用其被拉长后中间部分横截面面积减小为A′,则结构的名义应力仍为F/A。该方法是以名义应力为基准,针对不同构造细节通过试验方法获得不同名义应力水平下的疲劳特性和疲劳寿命,由此得到的应力水平与疲劳寿命的关系曲线即为S-N曲线。获得S-N曲线后,根据桥梁实测荷载谱,按照疲劳损伤理论分析构件的疲劳特性,获得相应的疲劳寿命。在采用有限元模型计算时要考虑结构的大开孔及大缺口等宏观形状,受弯构件的名义应力的计算公式为:

式中:F——截面所受轴向力;
M——截面上的弯矩;
A——横截面积;
I——截面惯性矩;
y——结构中性轴到研究部位的距离。
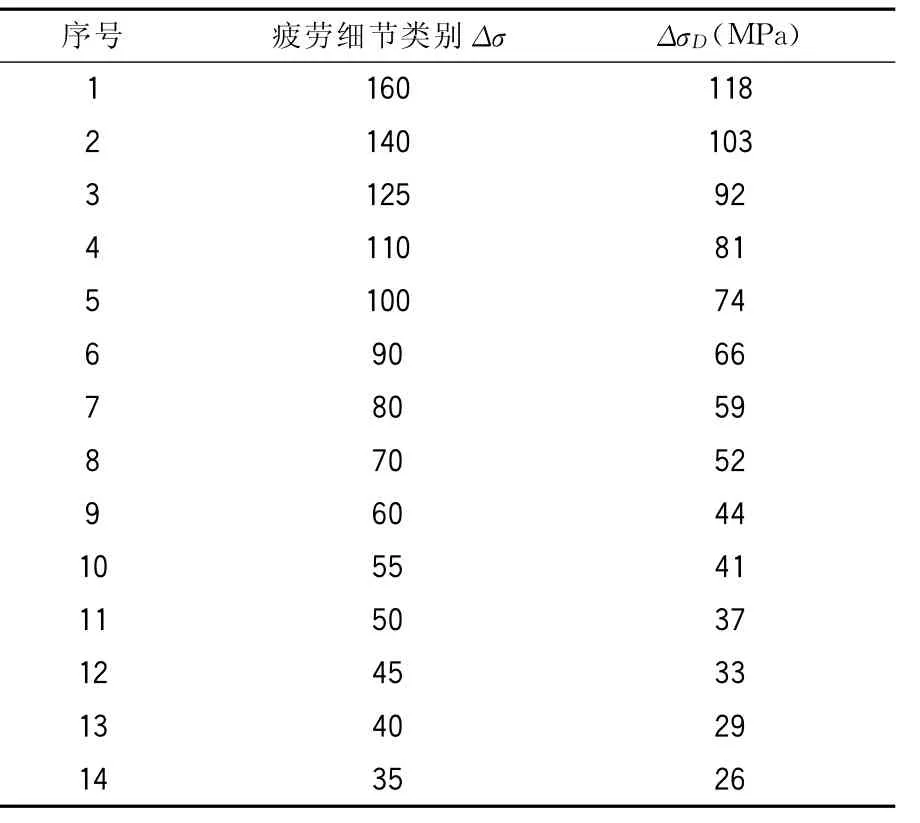
表1 我国规范构造细节分类表
采用该方法分析钢桥疲劳状况时,首先要确定构件的构造细节,然后再结合规范中所规定的该构造细节的S-N曲线计算分析。由于S-N曲线要通过试验获得,而疲劳试验十分昂贵,因此只有常用的构造细节才用做疲劳试验,而随着桥梁结构形式的多样化发展趋势,目前正在设计的一些大跨度钢桥中的构造细节在各国的规范中均未有明确规定,所以相关构造细节的力学及疲劳性能亟需被探明。
我国规范将钢桥疲劳构造细节分为14类,以200万次循环时的疲劳强度作为每个疲劳构造细节的分类,疲劳强度在36~140 MPa之间,如表1所示。但规范中对疲劳部分的条文说明较为粗糙,得出的疲劳设计曲线却没有给出各个寿命区段的表达式,在疲劳寿命为1×107~1×108之间的应力幅计算公式没有给出,两个重要参数即常幅疲劳极限ΔσD和疲劳截止极限ΔσL的计算也未有说明,设计者在使用此曲线时只能参考欧洲规范中ΔσD和ΔσL的计算方法。因此我国规范虽然给出了疲劳设计曲线,但是相应的条文说明还有所欠缺。
2 悬索桥疲劳构造细节分析
本研究中的大跨径悬索桥主桁杆件采用全焊钢桁架结构,导致盖板对接焊缝与竖板对接焊缝相交,出现了各国规范均未涉及的构造细节,因此,本研究针对全焊钢桁梁焊缝交叉部位过焊孔新型关键构造细节进行疲劳分析。研究提出两种过焊孔构造细节形式,即圆弧过渡和直角过渡,如图3所示。
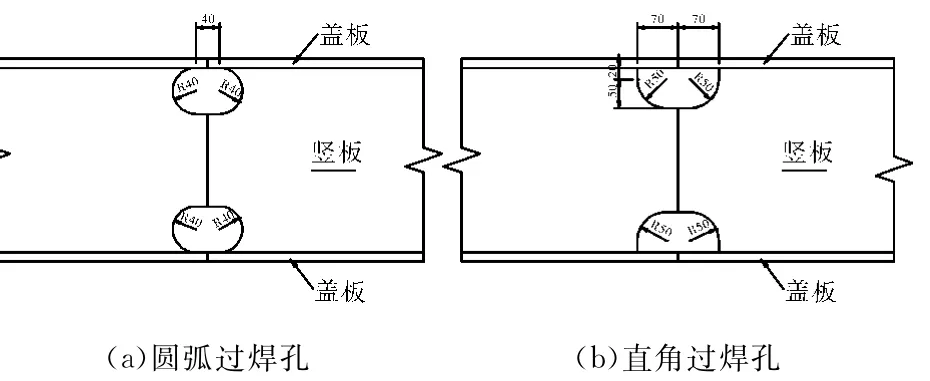
图3 主桁杆件过焊孔构造细节形式示意图
2.1 主桁杆件不同构造细节疲劳性能分析
根据ANSYS Workbench中的疲劳分析模块建立悬索桥钢桁梁圆弧过渡和直角过渡过焊孔构造细节模型。构造细节中的桁架杆由Solid186建模,用四边形进行网格划分,在关键构造细节处对网格加密,圆弧过渡过焊孔模型共划分180 498个节点,37 502个单元;直角过渡过焊孔模型共划分1 146 683个节点,27 947个单元。有限元模型中一端约束所有自由度,对称端加载2 500kN拉力,圆弧和直角构造细节的有限元模型见下页图4。

图4 圆弧和直角过渡过焊孔构造有限元实体模型图
计算结果如图5所示,圆弧过渡构造和直角过渡构造应力峰值均出现在过焊孔处。圆弧过渡构造在盖板上过焊孔起弧处峰值应力高达307.9 MPa,对应的名义应力达到144.7 MPa,应力集中系数超过了2,达到2.13,此构造细节应力集中情况明显,过焊孔的存在削弱了截面有效面积,由此导致局部应力集中发生。直角过渡构造在盖板上过焊孔起弧处峰值应力高达241.7 MPa,对应的名义应力达到144.7 MPa,应力集中系数未超过2,达到1.67,盖板应力集中现象弱于圆弧过渡构造。圆弧过渡构造在竖板上过焊孔边缘峰值应力高达251.6 MPa,对应的名义应力达到169.4 MPa,应力集中系数未超过2,仅达到1.49。直角过渡构造在竖板上过焊孔边缘峰值应力高达241.5 MPa,对应的名义应力达到169.4 MPa,此时的应力集中系数未超过2,仅达到1.43。随着远离过焊孔边缘,两种构造细节在竖板上的应力均不断减小,圆弧过渡构造在离过焊孔边缘60mm处,竖板的应力降低到165.6 MPa;直角过渡构造在离过焊孔边缘60mm处,竖板的应力降低到168.5 MPa,两种构造细节此时的应力值与各自的名义应力十分接近。
计算结果表明,当外荷载相同,边界条件相同时,钢梁直角过渡过焊孔处应力集中系数、相同位置的应力峰值小于圆弧过渡,故对于主桁杆件的抗疲劳性能来说,直角过渡构造更为安全,因此对于大跨径钢桁梁悬索桥,桁架杆过焊孔构造宜设计为直角过渡构造形式。
2.2 直角过渡构造细节疲劳寿命分析
前节确定了主桁过焊孔构造宜采用直角过渡构造形式。本节采用Workbench计算此构造细节的疲劳性能,数值模拟该构造细节理论S-N曲线,得出该构造细节的疲劳寿命,相关几何模型见图6。
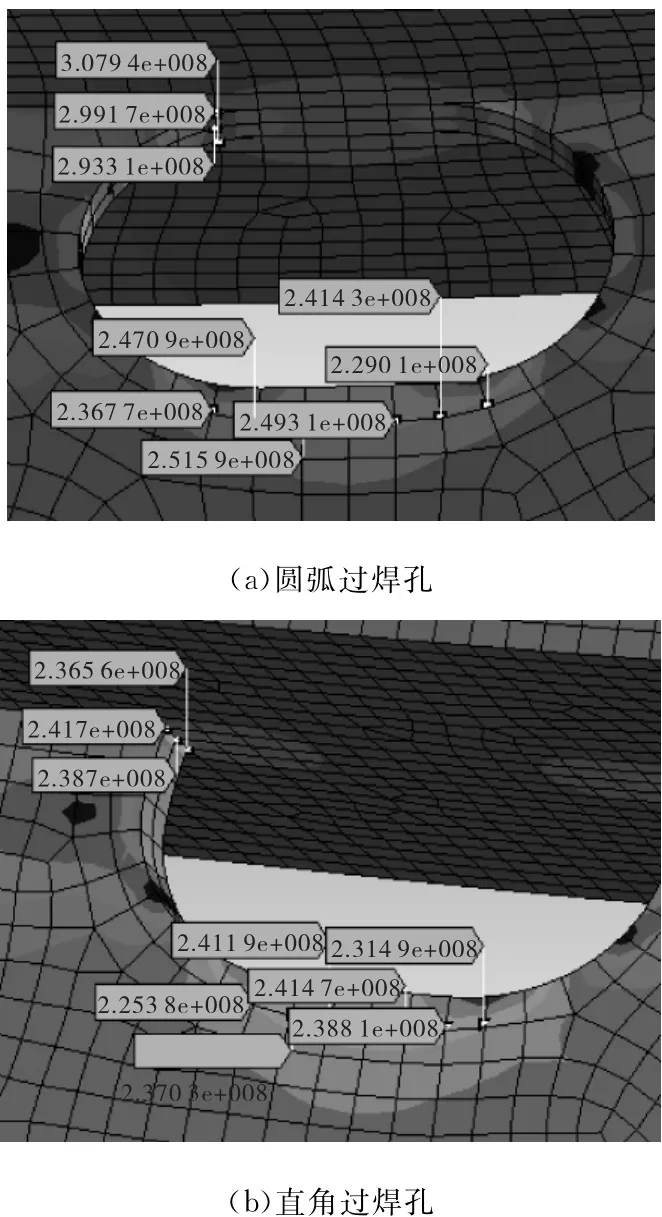
图5 圆弧与直角过渡过焊孔有限元计算结果示意图(Pa)

图6 未补强直角过渡构造细节几何模型图
未补强直角过渡构造细节由Solid186实体单元建模,用四边形网格单元划分为340 952个节点,75 264个单元。有限元模型中一端约束平动和转动所有自由度,对称端施加表2中的拉力荷载。有限元模型中,构件实际受到的拉力与构件屈服时的荷载之比为加载系数。依据加载系数的不同,模型中荷载共分为6个等级,即加载系数从0.2到0.7六级,每级按0.1递增。荷载循环方式为正弦波荷载,计算未补强直角过渡构造细节在各级荷载加载下的疲劳寿命。
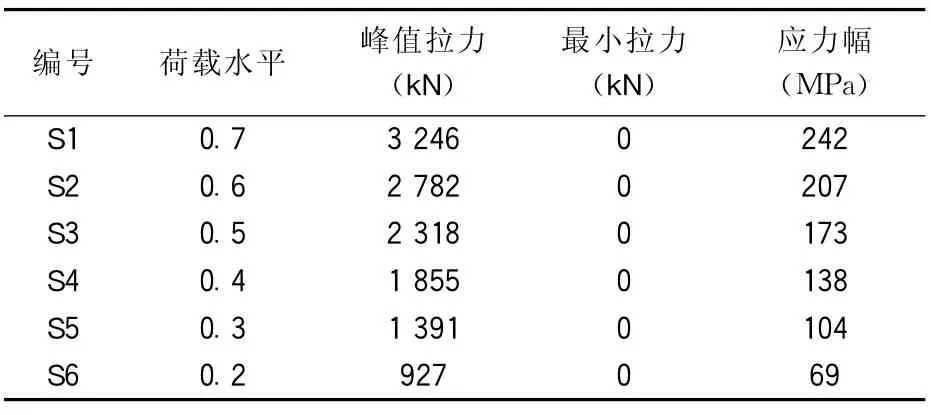
表2 未补强直角过渡构造细节加载荷载水平数值表
由表2可获得未补强直角过渡构造细节六个荷载水平下的等效应力云图和疲劳寿命云图,由于篇幅限制,仅给出加载系数为0.7时的构件等效应力云图及疲劳寿命云图,见图7和图8,疲劳裂纹起源于过焊孔周围。
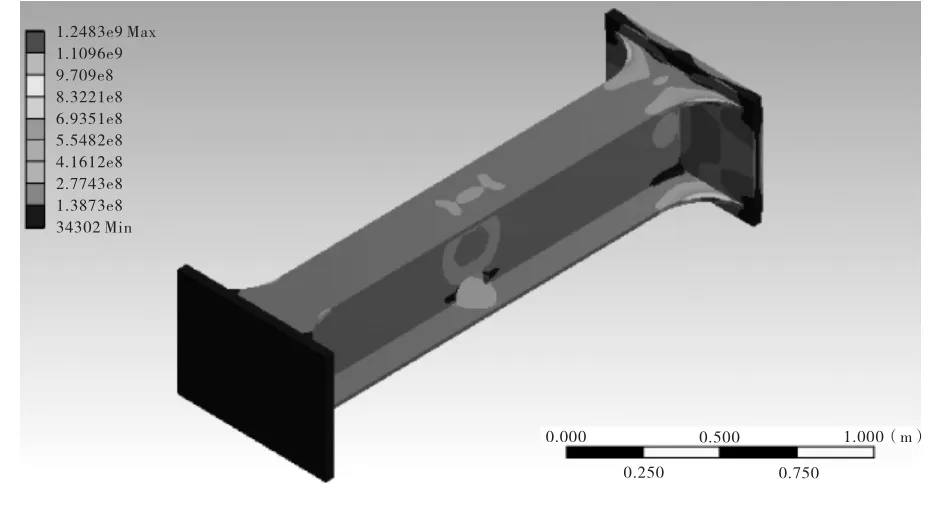
图7 S1加载水平下等效应力云图
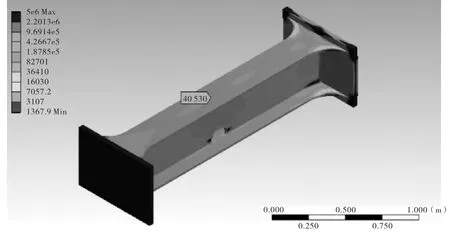
图8 S1加载水平下疲劳寿命云图
将S1~S6六个加载水平下未补强直角过渡构造细节过焊孔处的六组疲劳寿命数值进行汇总,将应力幅和构件过焊孔处最低疲劳寿命在对数坐标系下进行数据拟合,获得未补强直角过渡构造细节过焊孔疲劳寿命,见图9。
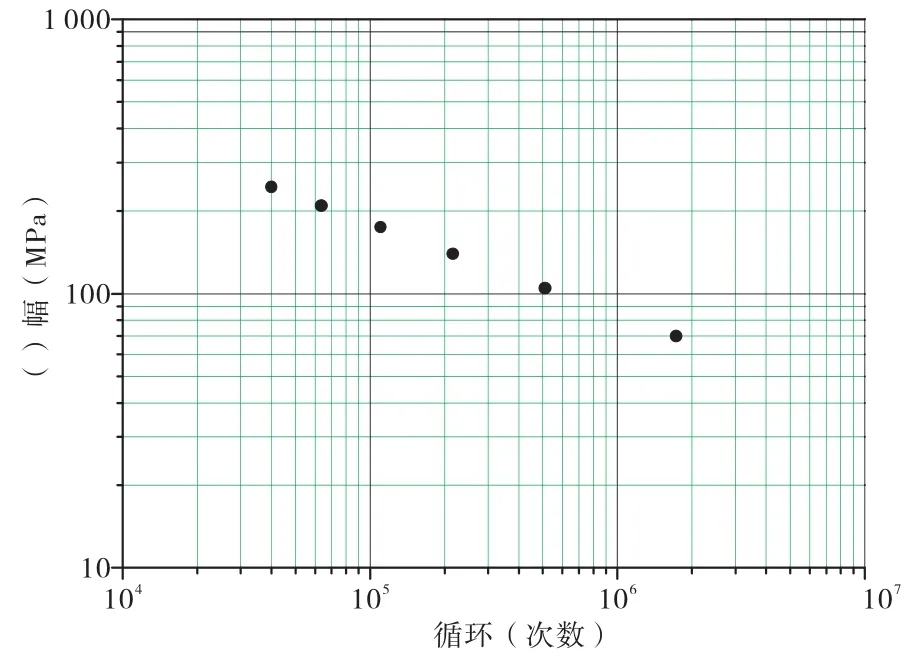
图9 未补强直角过渡构造细节疲劳寿命曲线图
由图9得到未补强直角过渡构造细节疲劳寿命的回归方程如式(2):

求得σ0(2×106)=66.47(MPa)
由式(2)可知,未补强直角过渡构造细节荷载循环200万次应力幅为66.47 MPa,对应的疲劳强度较低,若将此构造细节用于车流量大,荷载等级高的桥梁上,车辆往复荷载加载下必将产生疲劳损伤破坏,需采取相应的补强措施对该构造进行细节疲劳补强。
对于钢结构疲劳构件的补强,较为有效的方法分为两种:(1)封堵过焊孔法:此种方法封堵过焊孔的原理为增加截面的面积,进而降低截面处由过焊孔出现所引起的应力集中。但是此种方法对施工的操作工艺要求较高,在施工时如果操作不当,将会引起过焊孔周围出现很大的残余应力,导致新的疲劳问题出现。(2)疲劳补强板法:此种方法就是在构件的过焊孔两端增加补焊疲劳补强板,由于增加补焊的疲劳补强板与结构焊接处离过焊孔的距离较远,且增大了过焊孔处的面积,从而减小了相应的疲劳应力,并且对施工操作要求一般。综合上述特点,本研究采用疲劳补强板法对前节计算所得构造细节进行疲劳补强,计算直角过渡构造细节在各级荷载水平下的疲劳寿命。
疲劳补强后的直角过渡构造细节由Solid186单元建模,采用四边形网格单元共划分为356 737个节点,79 311个单元。有限元模型中一端约束平动和转动所有自由度,对称端施加下页表3中六个水平的拉力荷载。荷载循环方式为正弦波荷载,计算疲劳补强后的直角过渡构造细节在各级加载下的疲劳寿命。

表3 疲劳补强后直角过渡构造细节加载水平数值表
由表3可获得补强后直角过渡构造细节六个加载水平下的等效应力云图及疲劳寿命云图,由于篇幅限制,仅给出加载系数为0.7时构件等效应力云图及疲劳寿命云图,如图10~11所示。计算结果表明,增加疲劳补强板后直角过渡构造过焊孔处的应力集中现象消失,相应的应力值降低,应力最大的位置在盖板圆弧倒角处。

图10 T1加载水平下等效应力云图
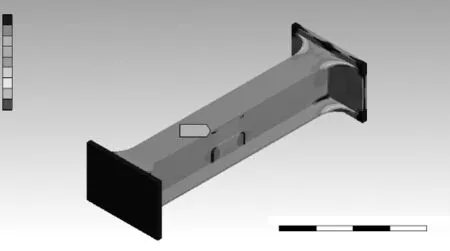
图11 T1加载水平下疲劳寿命云图
将T1~T6六个加载水平下补强后的直角过渡构造细节过焊孔处疲劳寿命的数值进行汇总,T1~T6六个荷载水平下补强后的直角过渡构造细节过焊孔的应力幅和循环次数见表4。

表4 补强后的直角过渡构造细节计算结果表
将应力幅和构件过焊孔处最低疲劳寿命在对数坐标系下进行数据拟合,获得补强后直角过渡构造细节过焊孔疲劳寿命,见图12。

图12 补强后直角过渡构造细节疲劳寿命曲线图
由图12可得到补强后的直角过渡构造细节疲劳寿命的回归方程式(3):

求得σ0(2×106)=89.66(MPa)
计算结果表明,疲劳补强后的直角过渡构造细节荷载200万次应力幅为89.66 MPa,比未补强直角过渡构造细节提高了34.9%,疲劳强度显著提高。
3 结语
(1)针对大跨径悬索桥钢桁梁盖板对接焊缝与竖板对接焊缝交叉部位过焊孔新型形式,研究提出了两种过焊孔构造细节:一种是圆弧过渡;另一种是直角过渡。通过有限元分析两种构造的受力性能和两种构造细节的疲劳特性,获得两种构造细节过焊孔处的应力集中程度:圆弧过渡构造的应力集中系数为2.13;直角过渡构造的应力集中系数为1.64。以此确定直角过渡构造细节适用于大跨径悬索桥钢桁梁主桁结构设计。
(2)未补强直角过渡构造细节荷载循环加载200万次的应力幅为66.47 MPa,安全系数较低。针对该构造细节提出疲劳补强措施,确定在过焊孔两端增加补焊疲劳补强板的方式进行疲劳补强。采用补强板补强后的直角过渡构造细节荷载200万次应力幅为89.66 MPa,比未补强直角过渡构造细节提高了34.9%,疲劳强度显著提高,因此对于大跨径钢桁梁悬索桥,推荐采用增加疲劳补强板的方法对钢桁梁主桁杆件盖板对接焊缝与竖板对接焊缝相交处过焊孔进行补强。
