基于带有ARCH效应时间序列分析的网络流量预测

杨 阳 朱浩然 任鹏飞

1(中国银联电子支付研究院 上海 201201)2(电子商务与电子支付国家工程实验室 上海 201201)3(恒安嘉新(北京)科技股份公司 北京 100089)

随着互联网技术的成熟和应用业务的飞速发展，网络用户数目逐渐增多，网络结构日趋复杂，业务场景的不断变化，给网络管理和异常检测都带来了很大的难度.如，我们发现在生产网络中有一些异常流量突发的状况，经分析，引起网络流量异常的原因主要有2类：分别是恶意攻击和瞬时的大量访问.其中恶意攻击即包括DDoS攻击和端口扫描等，还包括爬虫等业务程序对服务器的访问；瞬时的大量访问主要是业务活动时间节点、法定节假日等时间节点，突增的正常用户访问.恶意攻击行为会导致网络拥挤和过载，破坏网络正常访问.这些恶意攻击行为有很大一部分是模拟真实访问生成的，根据传统的异常特征检测难以发现.为了更好地检测流量中的恶意攻击行为，我们需要对网络流量数据进行分析和预测.

流量异常检测的基本思想是首先对正常数据源进行描述和分析，并构建流量预测模型，同时针对流量异常状况制定流量基线，然后根据实际流量偏离正常基线的情况作出预警.因此对于网络流量异常检测而言流量的准确预测非常重要，直接决定了网络异常检测的可靠性.常用的流量预测模型方法主要有时间序列分析、小波分析、神经网络等手段.

网络流量数据是一类随时间变化的数据，我们可以考虑用时间序列分析的方法对网络流量数据进行分析建模，并对网络流量异常进行监测和预警，具体模型包括AR模型、ARMA模型、GARCH模型等.

小波分析是一种时频分析方法，具有多维分辨率分析的优势，在时域和频域都有很好的表征信号局部特性的能力.小波分析在低频部分存在较低的时间分辨率和较高的频率分辨率，在高频部分存在较高的时间分辨率和较低的频率分辨率，对正常信号中含有瞬时反常态现象可以进行很好的拟合.通过小波变换的异常流量监测技术就是根据小波变换的多尺度特性，将流量分解到多个不同的频域下并进行重构，通过频谱能量的不同发现网络流量的异常，从而更好地发现网络流量中的异常行为.

基于神经网络的网络流量异常监测技术，根据神经网络自适应学习的能力来提取网络流量中异常行为的特征，将训练数据分为正常数据和异常数据，通过神经网络方法对数据集进行训练，得到网络流量正常和异常的行为模式，通过训练好的神经网络就可以对网络流量数据进行分类识别为正常和异常.

1 相关工作

网络异常检测是根据正常行为和入侵行为的不同来进行判断，而无论以何种方式进行入侵，都会伴随着网络端口流量的异常变化.通过与正常流量的相异度即可判断某流量是否为异常流量，进而可以判断是否为入侵行为.

针对异常流量检测，目前研究人员已经提出了诸多的检测方法，大致包括：1)基于阈值的异常检测.基于阈值的检测方法在网络管理中被广泛使用.该方法的主要思想是针对某一流量参数，给定一个最大阈值和一个最小阈值，如果观测到的参数值超出了阈值范围，则判定为异常流量.根据阈值的设定方法又分为恒定阈值检测和自适应阈值检测.恒定阈值检测是由Maxion等人[1]提出，针对网络流量的一些参数，如网络利用率和数据包大小等给出正常流量参数阈值，然后进行检测.这种方法的优点是简单易用；但是需要丰富的技术经验.李中魁等人[2]针对静态阈值方法存在的问题，提出一种多点检测异常统计量为基础的自适应阈值算法，该方法按照一定时间间隔对网络流量进行采样，动态地调整参数判定的阈值.这种方法可以利用现有成熟的统计理论，且可使用的流量种类多；但是这种方法阈值的边界难以确定，同时对流量发生的次序以及内在的联系不敏感，容易遭到破解[2].2)基于数据挖掘的异常检测.基于数据挖掘的检测方法则借助数据挖掘在特征提取上的优势，对网络流量进行处理，进而得到流量模型以用于异常流量检测.目前常用的算法包括分类、关联规则挖掘以及时间序列分析等.3)基于统计模型的异常检测.基于统计模型的检测方法是从正常的流量数据中分析各种参数，并假设其满足某种概率分布，然后进行异常流量检测.Ward等人[3]提出，若时间足够长，流量序列中各参数过程服从正态分布，再调整观测值界限之后即可对未知流量进行检测.这类模型能够自适应地对用户行为进行建模，并获得较高的准确率；然而如果需要精确刻画用户现实中复杂的情况，则模型会非常复杂.4)基于自相似特征的异常检测.自相似性是指特征周期性地表现出相似性.Leland等人[4]首次提出互联网流量在统计上是自相似的.在此基础上，Cheng等人[5]结合小波分析与HHT的方法，设计了一种自相似参数估计算法.

2 背景原理与模型设计

2.1 时间序列分析原理

自回归滑动平均模型(ARMA)是研究时间序列的主要方法，是由自回归模型(AR)和滑动平均模型(MA)混合而成.但自回归滑动平均模型假设残差服从同方差的假设，对于像网络流量这类波动性随时间变动的数据使用ARMA模型难以捕获方差变动的信息.而在对波动性建模中，广义自回归条件异方差模型(GARCH)对时间序列中出现的波动性变动与爆发的特性具有较好的拟合能力，得到极大发展.ARMA(p,q)模型的一般形式为

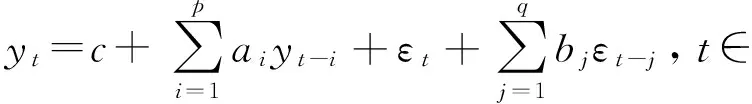
(1)

其中，εt为时刻t的残差，且εt～N(0,σ2)，c为常数，p,q为ARMA模型的阶数，ai,bj为待估计的自回归参数和滑动平均参数[6].ARMA模型是最常用的时间序列模型之一，在逼近许多平稳过程时表现出很强的适用性，同时对于数据的时间趋势和周期特征可以对数据进行差分，使其转化为平稳的时间序列数据.ARMA模型适合波动性小的非平稳时间序列，很难捕获外生变量对数据的影响.

某一时刻残差服从正态分布，此正态分布的均值为0，方差是一个随时间变化的量时称为条件异方差.并且这个随时间变化的方差是该时间点过去有限项噪声值平方的线性组合时，称为自回归条件异方差模型(ARCH)，Bollerslev对ARCH模型的改进而引进了广义自回归条件异方差模型(GARCH)，GARCH(p,q)模型的结构如下：

(2)

2.2 小波分析原理

小波分析是一种信号与信息处理的工具，是除傅里叶分析之外又一种时频分析方法.小波分析具有多分辨特性和时域局部化特征，因此既可以对时域分析又可以对频域分析，对处理非平稳信号有很强的适用性.设函数Ψ为一平方可积函数，Ψ∈L2(R)，如果傅里叶变换满足条件：

(3)

则称Ψ是一个基小波.设f∈L2(R)，称

(4)

(5)

式(5)中,dj,k=〈f(t),φj,k(t)〉称为小波展开系数，CJ,k=〈f(t),φJ,k(t)〉称为尺度展开系数[8].

2.3 模型构建

网络流量数据可以看作是一个时间序列数据，可以根据时间序列分析的方法对流量数据进行检测分析.

首先对网络流量数据进行时间序列的平稳性检验，并根据结果决定是否进行差分.由于虚假回归问题，在我们进行动态回归模型的拟合时，必须先对序列的平稳性进行检验，只有当序列通过平稳性检验时才能使用时间序列分析模型.检验的方法主要有DF检验、ADF检验、PP检验、协整检验等[9].对银联网络流量数据主要采用ADF检验的方法，ADF检验(augmented Dickey-Fuller)常用于对序列的自回归过程进行平稳性检验，对一个自回归过程：

xt=φ1xt -1+…+φpxt -p+εt,

(6)

其特征方程为

λp-φ1λp-1-…-φp=0.

(7)

若特征方程的根都在单位圆内，即

|λi|<1,i=1,2,…,p，

(8)

则说明序列平稳.若有单位根存在则序列非平稳，且可以推得自回归系数之和为1，因此通过自回归系数之后是否为1可以判断序列的平稳性.因此我们得到：

xt-xt -1=φ1xt -1+…+φpxt -p-xt -1+εt=

(φ2+…+φp)xt -1+φ1xt -1-xt -1-

(φ2+…+φp)xt -1+φ2xt -2+

(φ3+…+φp)xt -2-(φ3+…+φp)xt -2+

φ3xt -3+(φ4+…+φp)xt -3+…-

φpxt -p+1+φpxt -p+εt.

(9)

整理得：

(10)

其中：

ρ=φ1+φ2+…+φp-1,

(11)

βj=-φj+1-φj+2-…-φp,j=1,2,…,p-1.

(12)

如果序列平稳，则ρ<0，若不平稳，则ρ=0.则单位根检验的假设条件为

H0:ρ=0(序列非平稳)↔H1:ρ<0(序列平稳).

构造统计量：

(13)

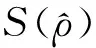
其次根据网络流量波动性大的特征，我们采用小波变换分解与重构的方法将网络流量分为低频项和高频项，并对各个子序列建立ARMA模型，确定模型的参数.

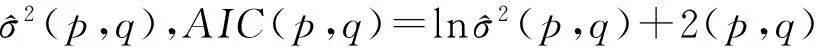
之后针对低频项和高频项进行ARCH效应检验，根据检验结果考虑是否建立ARMA-GARCH模型，具体为若不存在ARCH效应，则保留已建立的ARMA模型，若存在ARCH效应，则建立ARMA-GARCH模型.

对ARCH效应进行检验是一种特殊的条件异方差检验，其在要求序列具有异方差性的同时，需要异方差性是由某种自相关关系造成的，这种自相关关系可以由残差序列的自回归模型拟合得到.常用的ARCH效应检验的方法有PortmanteauQ检验、LM检验等[11].PortmanteauQ检验的假设为

H0：残差平方序列完全随机(方差齐性)↔H1：残差平方序列自相关(方差非齐).

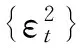
H0:ρ1=ρ2=…=ρq=0↔H1:ρ1,ρ2,…,ρq不全为0.

对PortmanteauQ检验统计量的构造为

(14)

其中,n为序列长度，ρi为残差序列延迟i阶自相关系数:

(15)

最后考虑特定的业务情况.针对网络流量业务上合理的激增时间点，加入激增项.最终将各个序列建立的模型进行线性叠加得到网络流量预测模型，对未来的流量数据进行预测，并根据制定的检测基线对网络流量异常进行检测并予以预警.

3 实证分析

选取2016-7—2017-10的银联网络流量数据作为数据源，以2016-7—2017-6数据作为模型构建，以2017-7—2017-10数据作为测试验证.

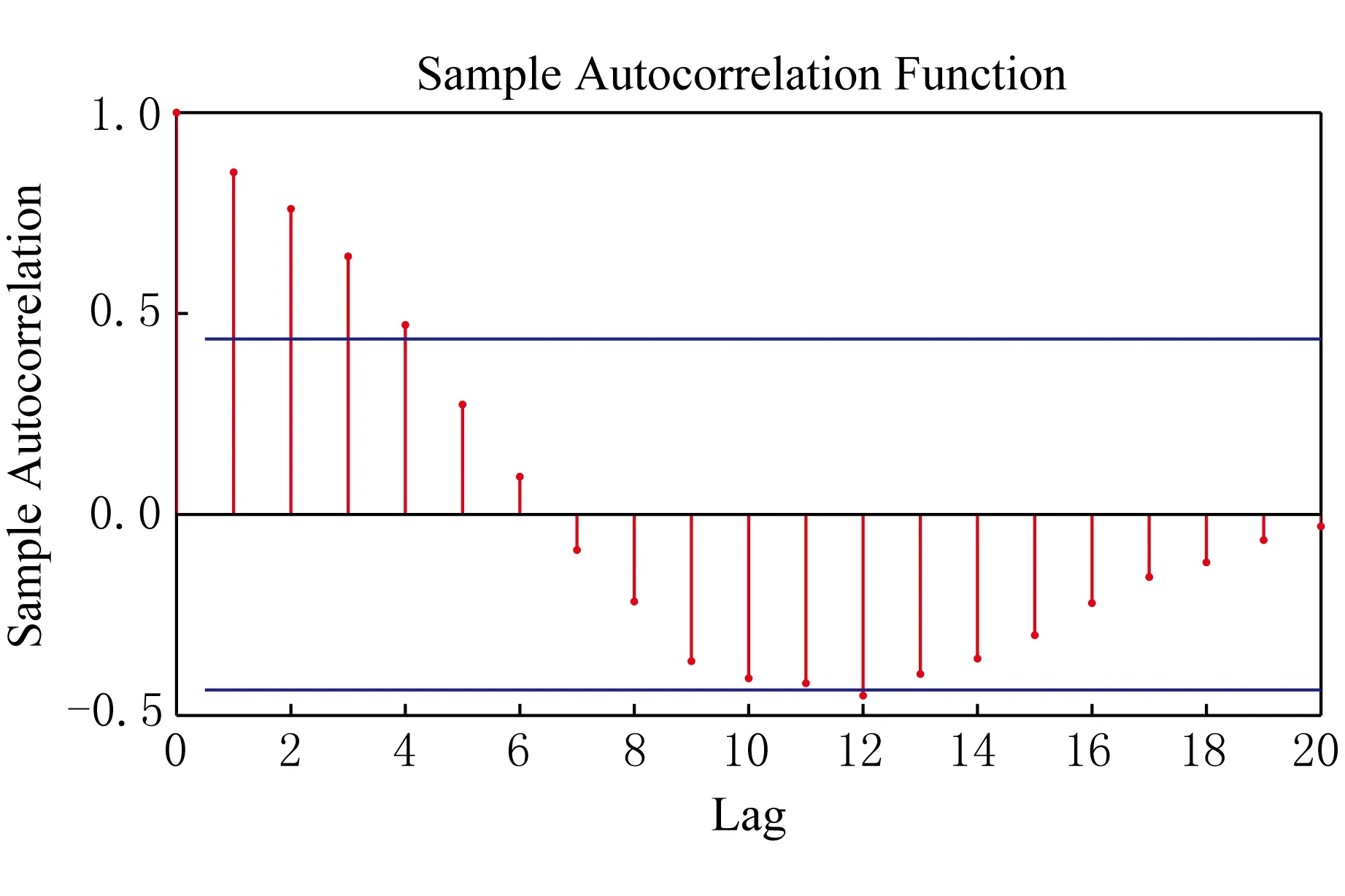
图1 自相关图

1) 首先对数据进行ADF单位根检验，检验数据的平稳性，检验结果接受原假设，需要对数据进行差分，二阶差分后时间序列数据平稳.

2) 对网络流量时间序列数据通过小波分析进行分解与重构，得到低频序列和高频序列[13].在对最优小波基和分解尺度的选择上，采用时频紧支集和高正则性的Daubechies小波基函数[14]，确定尺度为3的分解并对单支进行重构，得到3个序列，包括1个低频序列和2个高频序列，低频序列定义为L1，表示网络流量的趋势项，高频序列定义为H1,H2，表示网络流量的周期性和随机性.

3) 确定自相关和偏相关系数.以高频序列H1为例，由于自相关系数和偏相关系数具有拖尾效应，考虑使用自回归移动平均过程ARMA模型.如图1及图2，回归系数逐渐减小至0附近，为拖尾.根据ARMA(p,q)中参数的显著性、极大似然估计、AIC准则、SC准则、残差的白噪声情况确定参数p=4，q=1.如图1及图2，自相关图为4阶拖尾，偏自相关图为1阶拖尾.

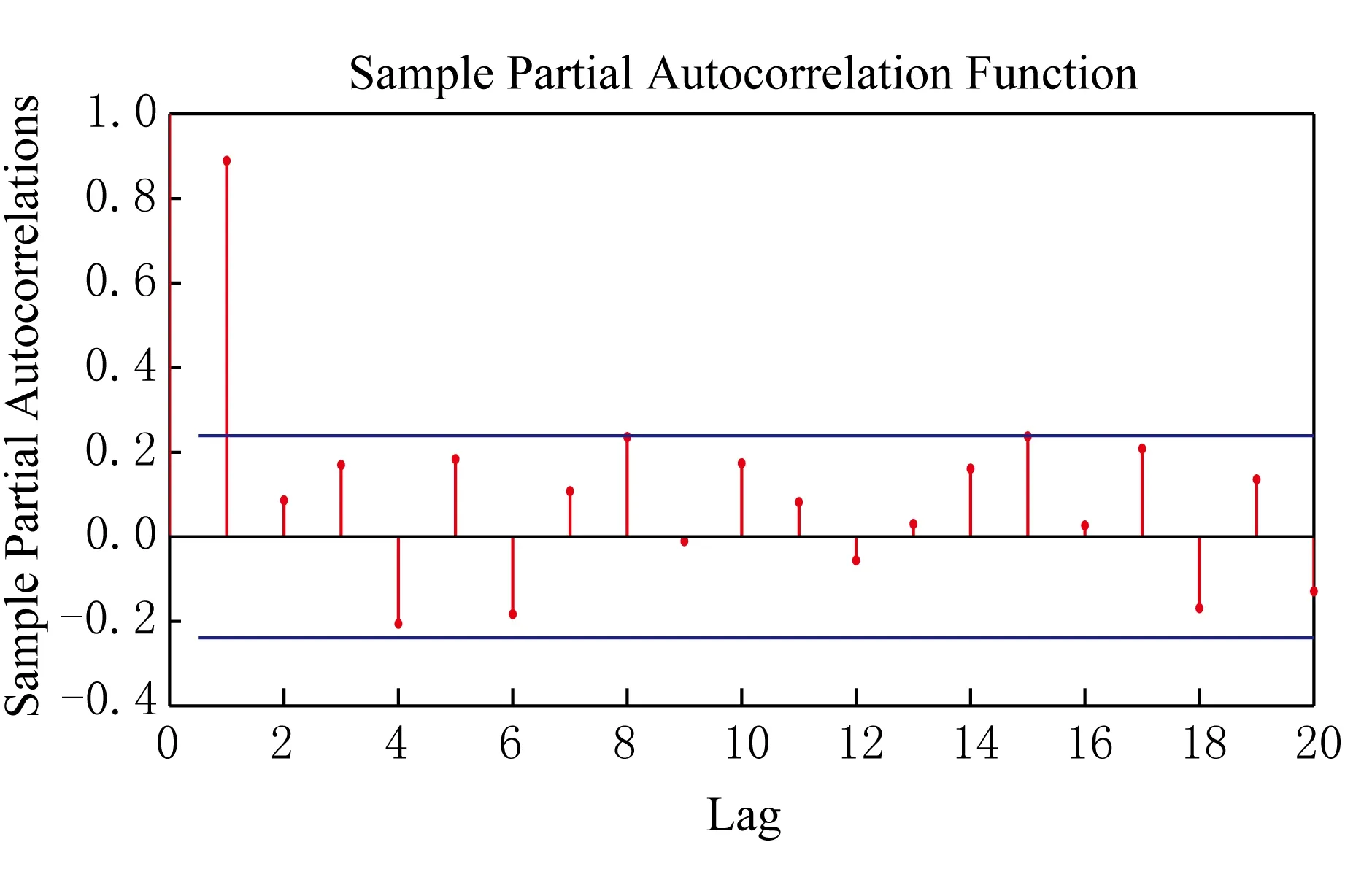
图2 偏相关图

yt=3.128yt -1-2.949yt -2-0.0193yt -3+

1.365yt -4+εt-2.479εt -1，

(16)

其中εt为残差序列.之后对模型的显著性和适应性进行检验，得到AIC为-0.3921，SC为-0.3102，表明数据是适应的.

4) ARCH效应检验.对序列ARCH效应检验的方法是拉格朗日乘子法检验.如果序列存在低阶ARCH效应，则考虑构建ARCH模型，如果序列存在高阶ARCH效应，则考虑构建GARCH模型.对序列的残差进行ARCH-LM检验，检验结果如表1所示.ARMA(4,1)的残差LM值为43.7973，相伴概率为0，小于显著性水平，拒绝原假设ARCH效应是显著的.对H1序列进行ARMA(4,1)-GARCH(1,1)建模.

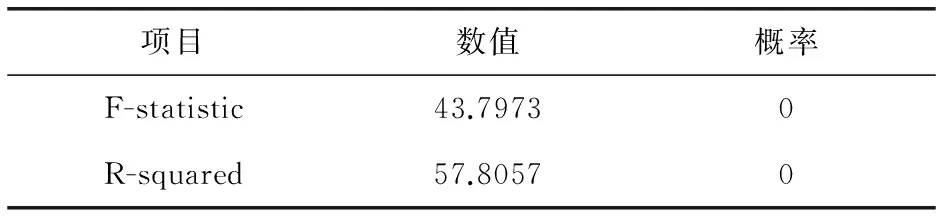
表1 残差的ARCH-LM检验结果

5) 引入激增项B(t).根据银联网络流量过往1年的历史数据，发现在“活动日”的流量有明显的激增现象，比如银联“62活动日”、“重阳活动日”以及“十一”黄金周和春节等.这类由于特定业务引起的流量激增现象无法通过时间序列模型拟合获取，但可以通过对过往历史数据的分析和业务场景的需要进行拟合，为了最终预测模型的准确性，我们通过在模型中引入激增项对该类突发的正常流量进行捕获.

6) 模型的建立.由于残差序列存在ARCH效应，采用GARCH进行建模，对模型参数进行拟合得到的结果如表2所示:

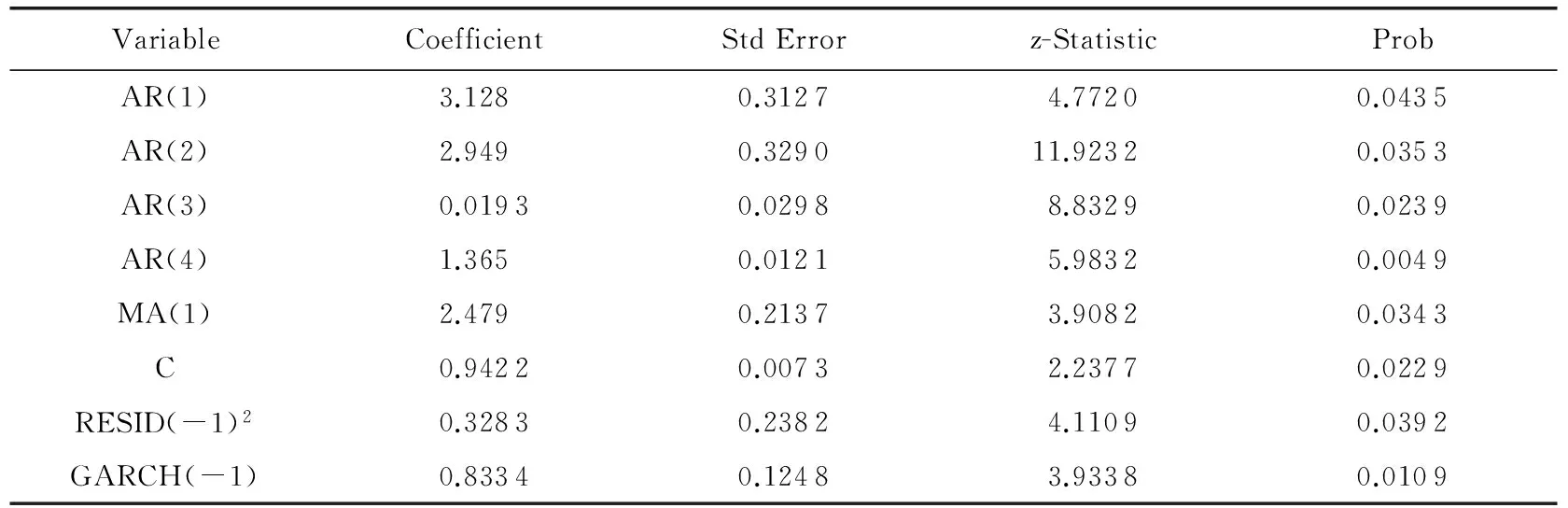
表2 ARMA-ARCH模型参数拟合结果[15]

由表2可知，所有参数的概率均小于0.05，说明GARCH模型的参数拟合是显著的.最终得到H1序列的ARMA(4,1)-GARCH(1,1)模型为

(17)

其中，εt为残差，et是独立同分布的标准正态分布随机变量，ht为残差的条件方差.

同理可以得到L1和H2序列的ARMA-GARCH模型.

对L1序列建立ARMA(2,3)-GARCH(1,1)模型，得到结果如下：

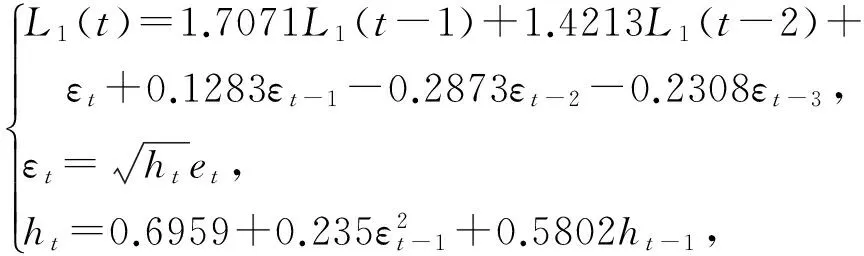
(18)

对H2序列建立ARMA(4,3)-ARCH(1)模型，得到结果如下：

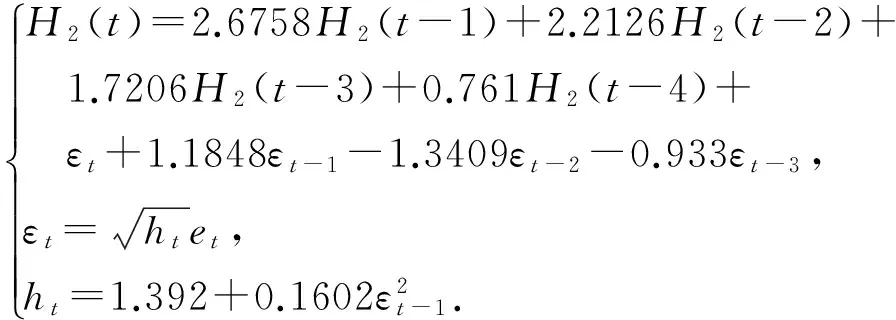
(19)

因此，网络流量模型为所有子序列模型的线性组合，具体公式如下：

Y(t)=L1(t)+H1(t)+H2(t)+B(t).

(20)

根据网络流量模型预测的网络流量和实际的流量序列图如图3、图4所示：

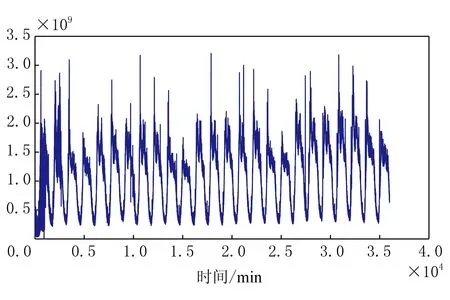
图3 实际流量时间序列

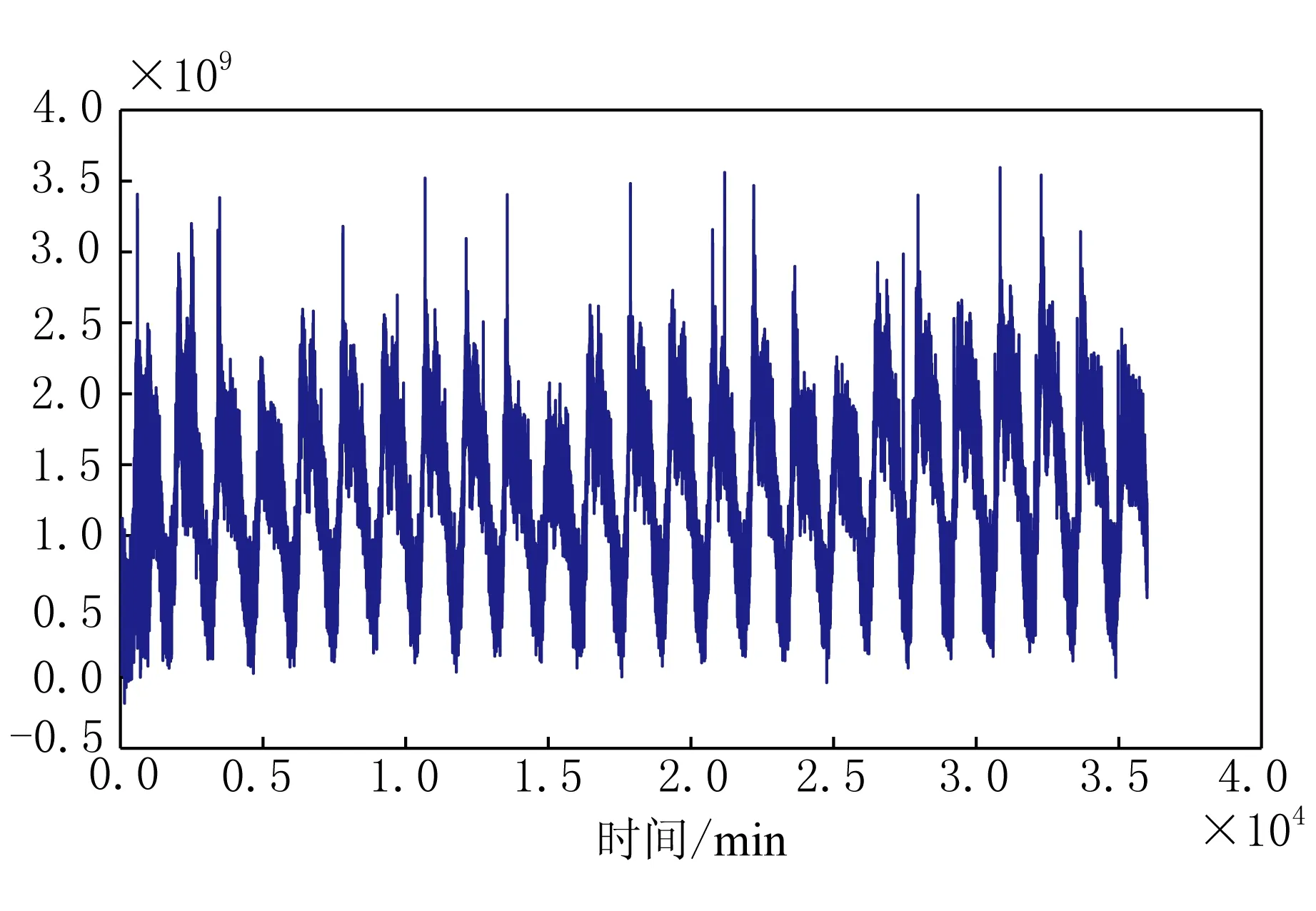
图4 流量模型预测序列

为了更好地说明通过小波的分解与重构提高了GARCH模型的准确性，我们选取了网络流量预测研究成果中比较新并且结果较好的方法来进行对比，再此额外构建了不含有ARCH效应的时间序列模型、没有通过小波分析分解与重构的ARMA-GARCH时间序列模型、结合小波分析与HHT的自相似特征预测模型.这几种模型的对比结果如表3所示：

表3 不同预测模型结果比较 %

从结果可以看出，本文构建的网络流量模型对数据的预测更优，估计的误差值更小，更能反映原始数据的波动情况，在此基础上对网络异常流量制定的基线阈值也更加准确.

4 结束语

本文采用小波分析和时间序列分析对2016-7—2017-10的银联部分网络流量数据进行分析与预测.首先对原始数据进行分解与重构，得到低频项和高频项，之后根据具体业务场景引入激增项，再将所有低频项和高频项依据各自特征用带有ARCH效应的时间序列模型进行建模，最终将各项进行组合，得到网络流量预测模型.通过与传统模型和实际数据进行对比，发现模型是有效并且准确的，为根据预测模型建立流量基线阈值提供了良好基础.

[1]Maxion R A, Feather F E. A case study of ethernet anomalies in a distributed computing environment. Reliability[J]. IEEE Trans on Reliability, 1990, 39(4), 433-443

[2]李中魁. 基于动态阈值的网络流量异常检测方法研究与实现[D]. 成都: 电子科技大学, 2010

[3]Ward A, Glynn P, Richardson K. Internet service performance failure detection[J]. Performance Evaluation Review, 1998, 26(3): 38-44

[4]Leland W E, Taqqu M S, Willinger W, et al. On the self-similar nature of Ethernet traffic[C] //Proc of ACM SIGCOMM Computer Communication Review. New York: ACM, 1993: 183-193

[5]Cheng X, Xie K, Wang D. Network traffic anomaly detection based on self-similarity using HHT and wavelet transform[C] //Proc of the 5th IEEE Int Conf on Information Assurance and Security (IAS’09). Piscataway, NJ: IEEE, 2009: 710-713

[6]王沁. 时间序列分析及其应用[M]. 成都: 西南交通大学出版社, 2008

[7]崔锦泰, 程正兴. 小波分析导论[M]. 西安: 西安交通大学出版社, 1995

[8]向杰, 程昌明, 张轶. 小波分析在时间序列中的分析应用[J]. 节水灌溉, 2013 (12): 15-17

[9]王振龙, 胡永宏. 应用时间序列分析[M]. 北京: 科学出版社, 2007

[10]潘贵豪, 胡乃联, 刘焕中, 等. 基于ARMA-GARCH模型的黄金价格实证分析[J]. 黄金, 2010, 31(1): 5-8

[11]肖云湘, 李星野. 基于小波的回归-GARCH模型及其在外汇储备中的应用[J]. 上海理工大学学报, 2015 (1): 18-22

[12]吴淑萍, 樊颖, 杨赞. 利率政策对房价的“非对称性”影响路径——基于小波分析和GARCH模型的研究[J]. 上海金融, 2017 (2): 3-10

[13]余健, 郭平. 基于改进小波神经网络的网络流量预测研究[J]. 计算机应用, 2007, 27(12): 2986-2988

[14]Aurea Gran, Helena Veiga. Wavelet-based detection of outliers in financial timeseries[J]. Computational Statistics and Data Analysis, 2010, 54(11): 2580-2593

[15]张永山. 基于小波多分辨率GARCH模型的汇率去噪预测[J]. 统计与决策, 2017 (12): 161-164