福建省科技创新全要素生产率动态实证分析——基于DEA-Malmquist指数模型和城市面板数据

李晓青

(厦门理工学院 经济与管理学院，福建 厦门 361024)

一、研究背景

随着知识经济时代的到来，科技创新成为推动区域经济发展的首要驱动要素，其发展水平和增长状况直接影响区域经济增长的速度与质量。作为东南沿海省份，福建省是我国实施创新驱动发展战略的重要区域，经济发展正处于从投资拉动到创新驱动的发展转型期。为加快创新型省份建设，十二五时期福建各级政府加大科技创新投入，自主创新和科技支撑转型发展能力显著增强。2015年《全国及各地区科技进步统计监测结果》显示，福建省科技活动投入指数全国排名第10位，科技活动产出指数第19位，综合科技进步水平指数第13位[1]。从这些指标不难看出，福建省科技投入与产出水平存在明显差距。福建省在增强科技创新能力的过程中，不仅要注重科技资源的总量增加，更要注重科技创新质量的提高。特别是在创新资源有限的情况下，科技创新质量就变得更为突出，提高创新效率和增强自主创新能力才是实现经济增长的主要动力和持久源泉。创新驱动战略为福建省经济发展既创造了机遇，也带来了挑战，福建省区域经济增长要实现可持续发展，务必重视科技创新效率的提升。因此，对福建省十二五其间的科技创新生产率开展动态研究并探寻变化的动因，对福建省科技创新管理具有十分重要的理论和现实意义。

科技创新效率是对区域创新体系总体效率的衡量，一般以测量全要素生产率(Total Factor Productivity，TFP)为基础。国外关于TFP的测度研究主要有参数方法和非参数方法。参数方法以素罗余值法、超越对数模型估计和随机前沿分析(SFA)为代表；非参数方法以数据包络分析(DEA)和基于DEA的Malmquist指数分析方法为代表。与参数法相比，非参数法无需设定具体的生产函数形式，无需主观赋权，在测量多投入多产出的决策单元(Decision Making Unit,DMU)相对效率方面具有优势。科技创新活动是一个多投入多产出的复杂生产过程，国内外学者多用非参数法来测算科技创新全要素生产率。相对于DEA只能在截面上进行静态效率评价，在DEA基础上提出的DEA-Malmquist指数分析模型能够利用不同决策单元的跨期面板数据进行动态分析，近些年来受到国内外学者的青睐。国外研究例如Sun等[2]、Hashimoto等[3]、Guan等[4]、Claudio等[5]、Han等[6]等，均利用DEA-Malmquist指数模型对创新效率及全要素生产率变化进行了研究。在科技创新全要素生产率测度方面，国内代表性研究有刘凤朝和潘雄锋[7]、王珍珍和黄茂兴[8]、刘明广[9]、朱鹏颐等[10]、向小东等[11]，DEA-Malmquist指数模型为科技创新全要素生产率测度提供了较好的解决方法。目前，关于福建省区域科技创新效率的实证研究非常少，科技创新全要素生产率研究更为缺乏。袁博使用随机前沿分析(SFA)测度了福建省各地区创新型企业创新效率[12]，朱鹏颐等运用超效率数据包络分析视窗模型和Malmquist指数对福建城市科技创新效率进行了评价研究[10]。鉴于此，为完整全面地分析近年来福建省科技创新效率的动态发展变化，笔者采用DEA-Malmquist指数模型对福建省2011—2016年其间9个地级市的面板数据进行分析，测量福建省科技创新全要素生产率变动情况，为科技决策者找到效率变化的主要动因，同时也给决策单元如何改进、提高科技创新效率指明方向。

二、DEA-Malmquist指数模型

全要素生产率(Total Factor Productivity，TFP)的一般含义是资源投入开发利用的效率，DEA-Malmquist指数模型是一种用于分析多投入多产出决策单元的全要素生产率变化及其原因的有效方法。Malmquist指数最早由瑞典经济学家Malmquist提出[13]，后来Caves、Christensen和Diewert将其用于测量全要素生产率变化[14]，Fare进一步采用DEA方法来测算并分解Malmquist指数[15]，从而形成了DEA-Malmquist生产率指数模型。此后，该模型被广泛用于测算全要素生产率(TFP)的变动。该方法的基本思路是采用投入—产出数据构造成生产前沿面函数，通过DEA的非参数线性规划模型求解距离函数，通过计算每个决策单元(DMU)分别在t期和t+1期与生产前沿的距离来表示两个不同时段的生产率变化，从而得到相对效率的变动。

笔者将福建省9个地级市作为单独的生产决策单元(DMU)，运用DEA-Malmquist指数构建各个时期科技创新生产的最佳前沿面，然后将每期的DMU生产状况与当期最优前沿面进行比较，分析全要素生产率的变化。全要素生产率变动指数(TFP change,tfpch)计算公式如下：

(1)

其中，Xt、Yt分别表示决策单元在t期的投入指标和产出指标，Dt(Xt,Yt)是以t期的技术为参照表示的第t期的距离函数，Dt(Xt+1,Yt+1)是以t+1期的技术为参照表示的第t期的距离函数，Dt+1(Xt,Yt)、Dt+1(Xt+1,Yt+1)以此类推。Tfpch>1说明TFP呈增长趋势，科技创新效率提高；Tfpch<1说明TFP呈下降趋势，科技创新效率下降。

假设规模报酬不变(Constant Returns to Scale,CRS)，通过等价变化，Malmquist指数(tfpch)可以分解为综合技术效率变动指数(efficiency change,effch)和技术进步变动指数(technical change,techch)。(1)可分解表示为：

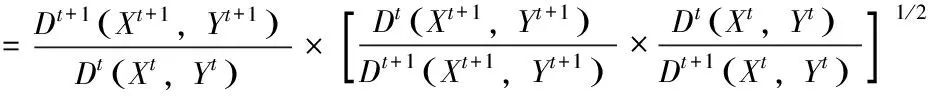
=effch×techch

(2)

在规模报酬可变(Variable Return to Scale,VRS)情况下，综合技术效率变动指数effch可以进一步分解为纯技术效率变动指数(pure technical efficiency change,pech)和规模效率变动指数(scale efficiency change,sech)。(2)可进一步分解为：

(3)

全要素生产率变动指数(tfpch)分解为综合技术效率变动指数(effch)和技术进步变动指数(techch)。effch衡量了决策单元从t时期到t+1时期科技创新要素投入配置效率的变动程度，反映生产决策单元对生产前沿面的追赶程度。当effch>1，表示与上一期相比当期生产更接近前沿面，技术效率改善；当effch<1，表示与上一期相比当期生产更远离前沿面，技术效率恶化。techch衡量决策单元从t时期到t+1时期生产前沿面的抬升变化，反映了技术水平的变化。当techch>1，表示与上一期相比决策单元技术水平有了进步；当techch<1，表示与上一期相比决策单元技术水平退步了。

在规模报酬可变的假设下，综合技术效率变动指数(effch)进一步分解为纯技术效率变动指数(pech)和规模效率变动指数(sech)。前者表示决策单元资源配置、组织变革和经营管理水平对效率变动的影响，反映的是在既定的资源投入和技术水平下要素的利用程度和资源配置效率；后者表示决策单元现有规模向最优生产规模靠拢的变化情况，反映的是在既定技术水平下要素投入规模的合理化程度。

三、实证研究

(一)指标选取及数据来源

测度全要素生产率要选取投入和产出指标，根据DEA分析理论，一般来说，DMU的数量不应少于投入和产出指标数量之和的两倍，否则DEA会失去对DMU效率的区分能力[16]。考虑到模型的区分度，分别选择2个投入指标和2个产出指标。科技创新是原创性科学研究和技术创新的总称，科技创新活动是一个多投入多产出的复杂系统。因此，投入产出指标的选取必须考虑到“研发性”和“创新性”特征。本研究从资金投入和人才投入方面分别选取R&D(研究与试验发展)资本存量(亿元)(x1)和每万名劳动力中R&D人员折合全时当量(人年)(x2)作为投入指标，从科技创新直接成果和科技创新价值贡献两方面分别选取专利申请授权量(件)(y1)和高新技术产业增加值(亿元)(y2)来作为产出指标。

R&D经费内部支出是衡量当期研发创新资金投入的重要指标，但考虑到资金投入对科技创新的影响不仅仅表现在当期，对以后若干时期的科技创新也有重要影响。由于它是一个流量指标，因此本研究在度量科技创新投入时将R&D经费内部支出换算为R&D资本存量，R&D资本存量的测算一般采用永续盘存法(Perpetual Inventory Method,PIM)[17-18]。测算公式是：RDit=(1-δ)RDi(t-1)+Ei(t-1)，其中，RDit表示i地市第t期的R&D资本存量，Ei(t-1)表示i地市第t-1期的R&D经费内部支出，δ表示研发资本折旧率。期初R&D资本存量值为：RDi0=Ei0/(g+δ)，g为研发资本增长率(假定等于E的年均增长率)；参考朱有为等[18]、吴延兵的研究[19]，δ取15%。本研究将基年定为2010年，在测算研发资本存量之前，先采用研发价格指数将R&D经费内部支出平减为以2010年为基期的不变价。研发价格指数计算式为：RDPI=0.75P+0.25W，P为工业生产者出厂价格指数(PPI),W为消费者价格指数(CPI)。此外，高新技术产业增加值也以2010年为基期采用工业生产者出厂价格指数(PPI)进行相应平减。

福建省9个地市2010—2016年各投入产出指标面板数据来源于《福建统计年鉴》、福建省统计局及各地市统计局网站统计信息公开数据、福建省科技厅及各地市科技局网站统计信息公开数据、福建省知识产权局网站专利统计信息以及各地市国民经济与社会发展统计公报。历年价格指数数据来源于《中国统计年鉴》。科技创新投入产出指标的基本情况如表1。可以看出，投入产出指标的标准差比较大，这也说明福建省科技创新发展水平有较大的地区差异。

表1 福建省9地市科技创新投入产出指标的描述统计

(二)不同年度福建科技创新全要素生产率变动及其分解

利用DEAP2.1软件对福建省9地市科技创新生产的面板数据进行Malmquist指数分析，测算得到年度平均的福建省科技创新全要素生产率变动指数及分解(见图1和表2)。总体而言，考察其间福建省科技创新全要素生产率(TFP)整体上比较平稳，年均略微下降0.5%。分解来看，综合技术效率提升，年均增长3.7%，同时技术进步水平下降，年均下降4%。两者变化幅度相当，作用相互抵消，导致全要素生产率无明显变化，略微有所下降。

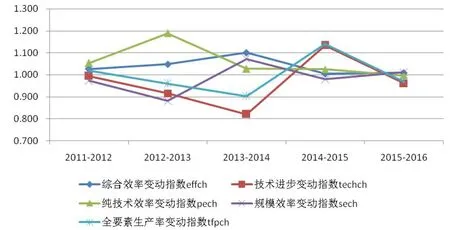
图1 2011—2016年福建省科技创新Malmquist生产率指数及分解指数均值趋势

进一步分析，2011—2016年科技创新全要素生产率呈现波动变化趋势:2011—2012年，生产率增长2%;2012—2014年均连续下降4%和9.7%;2014—2015年增长14%;2015—2016年又下降3.1%。全要素生产率变动指数可分解为综合技术效率变动指数和技术进步变动指数。综合技术效率变动指数均大于1，这说明考察期内各年度综合技术效率均得到提升。综合技术效率变动与技术进步变动趋势存在显著差异，表现为多数时期内当技术效率增长时，技术进步处于下降期，这说明福建省对现有研发创新技术的推广和扩散不太成功。全要素生产率变动指数同技术进步变动指数变化趋势一致(见图1)，可见，技术进步是科技创新全要素生产率变动的主要驱动因素。考察期内技术水平前沿面平均下降了4%，其中，除2014—2015年外，其余时期技术水平均出现退步。这里需要指出的是，这里的技术退步是指狭义的技术退步，DEA-Malmquist指数模型所测算的全要素生产率变动并不包括科技投入部分的技术进步，技术进步变动指数反映的是投入以外部分的技术水平变动，例如管理水平、组织创新、专业化和生产创新等。确切的说，技术水平下降说明出现了不包括投入的技术退步，但包括投入在内的技术进步是可能存在的[20]。随着科技投入的不断增加，在研发创新没有突破性进展的情况下，创新空间逐渐减少，这时需要更多的创新投入才能获得与原来相同的产出，导致生产前沿面的下移[19]，拖累了全要素生产率的增长。这一结论也说明2011—2016年福建省的科技进步为体现型技术进步，主要是依赖于科技投入要素的积累，并非单纯的技术进步力量起作用。但是，2014—2015年间福建科技创新全要素生产率显著增长14%，这种科技进步即为单纯的技术进步力量推动。

表2 2011—2016年科技创新Malmquist生产率指数及其分解指数均值

表2显示，综合技术效率年均增长了3.7%，福建省科技创新资源配置效率得到了改善，主要源自两方面的作用：纯技术效率年均增长了5.6%，规模效率sech年均下降了1.8%，纯技术效率的变动幅度超过了规模效率的变动，这说明纯技术效率的提升是技术效率出现正增长的主要动力。随着创新驱动战略的推行，福建省加大科技创新投入，注重创新内涵建设，科技创新体系在资源配置、组织变革和经营方面改善显著，但是生产规模合理化程度有所下降。这说明在扩大科技投入的同时，应该重视生产规模的控制，改变当前投入规模盲目扩大的粗放型增长方式，向集约型转变。

(三)不同地级市福建科技创新全要素生产率变动及其分解

2011—2016年福建省9个地级市的科技创新Malmquist指数及分解情况(见表3)。整体看，考察其间科技创新全要素生产率平均下降0.5%。从各区域来看，城市科技创新发展不均衡，区域差异明显。5个城市全要素生产率变动指数大于1，从高到低依次是福州、漳州、南平、龙岩和泉州，提升幅度最大的是福州，年均增长率达到8.4%，提升幅度最小的是泉州，增长率为0.9%；厦门、莆田、三明和宁德全要素生产率变动指数小于1，全要素生产率降幅最大的是莆田，下降15.5%。根据表3中全要素生产率变动指数的分解，笔者将生产率正向增长的5个地级市分为两类：一类是资源配置效率驱动型，如福州、漳州、南平和龙岩科技创新全要素生产率的增长主要来自于资源配置效率的驱动，而不是技术进步；另一类是技术进步驱动型，如泉州科技创新生产率提升0.9%，主要由技术进

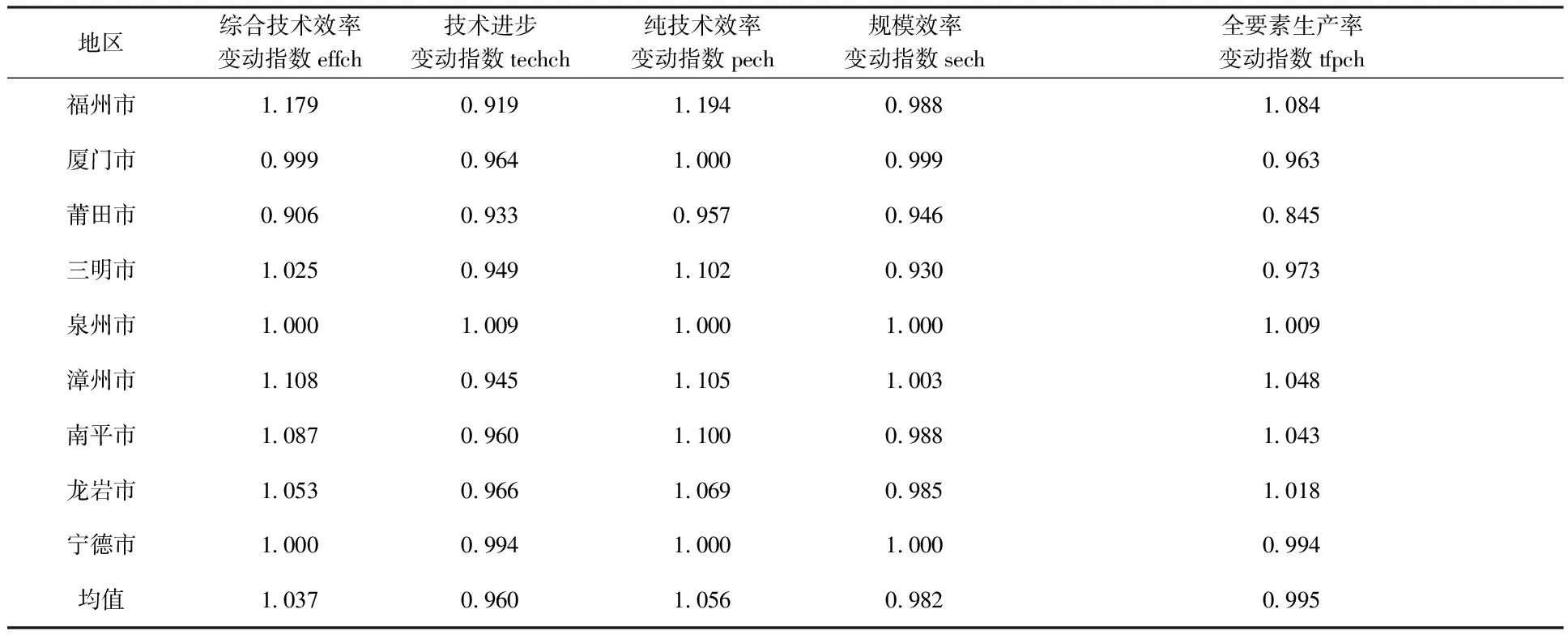
表3 2011—2016年福建省各地级市科技创新Malmquist生产率指数及其分解指数均值

步驱动。全要素生产率负增长的地级市有4个，根据造成生产率下降的原因也可以分为两类：一类是资源配置效率和技术衰退共同阻滞型，厦门和莆田属于这一类型，两地的资源配置效率和技术水平均退步，共同影响生产率下降；另一类是技术衰退阻滞型，三明和宁德属于这一类型，随着整体科技创新水平的提升，两地的生产前沿面相对后移，两地的科技创新全要素生产率下降主要归因于技术退步。上述分析显示，没有出现资源配置效率和技术进步“双驱动”的情况，这也说明福建各城市自身的科技创新发展存在不均衡，技术效率的改善和技术水平进步不能兼顾。

从各地区综合技术效率变动情况来看，莆田综合技术效率下降明显，下降幅度为9.4%；厦门和泉州保持稳定，其余城市综合技术效率均得到提升，这说明福建省大部分地级市的科技创新资源要素配置效率得到提升。从技术进步变动来看，除了泉州技术进步变动指数大于1，生产前沿面略有抬升，其他城市技术进步变动指数均小于1，呈现技术退步。如前所述，这里的技术进步反映的是科技创新投入要素以外的科技进步水平，这至少说明福建省大部分城市自主创新实力存在不足，如果不考虑投入要素的积累，单纯的技术进步较为薄弱，无法抬升有效前沿面。进一步地，根据DEA测度原理，综合技术效率的变动是纯技术效率和规模效率共同推动的。表3显示，福建省大部分地市纯技术效率变动指数大于1，而规模效率变动指数小于1。大部分地级市的科技创新综合技术效率的提升由纯技术效率的提升所驱动,而生产规模损失拖累了综合技术效率的增长。

进一步根据传统地域区划，将福建省9个地市划分为闽东、闽西、闽南和闽北四大区域来分析。闽东包括福州和莆田，闽西包括三明和龙岩，闽北包括宁德和南平，闽南包括厦门、漳州和泉州。根据计算结果(见表4)，四大区域的科技创新全要素生产率均有提升，总体上研究其间福建省科技创新政策和创新投入提升了区域科技创新水平。从推动力看，闽东主要由资源配置效率驱动，闽南和闽北主要由技术进步驱动，闽西由资源配置效率和技术进步共同驱动。四大区域中，闽东全要素生产率提升幅度最大，增长率为7%。以福州为中心的闽东地区科技创新效率进步最快，主要源于科技资源配置效率的大幅提升，但是投入要素以外的科技水平退步，说明还存在自主创新能力的提升空间。闽南和闽北地区的生产率提升水平相当，约为4%。资源配置效率保持不变，全要素生产率提升由技术水平的进步贡献，这说明两地科技管理水平、组织创新、专业化和生产创新方面改善显著，自主创新能力得到增强。闽西区域的生产率提升2.3%，主要由综合技术效率的提升和技术进步共同拉动。

表4 2011—2016年福建省四大区域科技创新Malmquist生产率指数及分解指数均值

四、结 语

基于福建省9个地级市2011—2016年的科技创新投入产出面板数据，采用DEA-Malmquist指数模型对福建省科技创新生产率变化情况进行实证研究，将全要素生产率变动分解为技术进步变动、纯技术效率变动和规模效率变动，从技术水平、资源配置效率和生产规模方面来阐述十二五其间福建省科技创新效率的演化。主要得到如下结论：

2011—2016年，福建省科技创新全要素生产率总体上保持平稳，年均略微下降0.5%。技术水平的变动是全要素生产率变动的主要驱动力量，虽然综合技术效率的增长对科技创新全要素生产率增长产生了正面影响，但是被技术水平的退步影响所抵消，导致全要素生产率略微有所下降。除泉州以外的其他城市均出现一定程度的技术衰退，这说明福建大部分区域科技创新的产出增长仍然是依赖于创新投入要素驱动的增长方式，这种粗放型的增长方式将会阻碍福建省创新驱动战略的实施。因此，要真正提升福建省科技创新生产率水平，应该高度重视提升科技自主创新能力，获取投入要素以外的技术进步，坚持将经济发展动力从投资驱动、要素驱动向创新驱动、效率驱动转化。近年来，福建省科技创新发展迅速，但是技术水平仍然在较低层次徘徊，要真正提升技术水平，应该寻求研发创新的进一步突破。在全球一体化背景下，除依靠自主研发外，另外一个途径就是技术转移或技术外溢，主要可以通过国外技术引进、国内技术购买及外商直接投资企业研发活动等实现对先进经验和技术的高效吸收和有效利用。此外，福建省整体上综合技术效率有所提升，纯技术效率增长是其主要推动力，但是规模效率下降一定程度拖累了技术效率的增长。福建省在加大科技投入的同时，需要关注生产规模与投入产出的匹配程度，调整产业结构，靠近最优生产规模水平，促使科技创新生产从“粗放化”向“集约化”转变。

福建省科技创新全要素生产率增长呈现出明显的区域差异。从城市角度分析，9个地级市的全要素生产率增长存在明显差异，其驱动因素也存在不同。福州、漳州、南平、龙岩和泉州的全要素生产率呈现正增长，其中，福州、漳州、南平和龙岩的生产率增长是由资源配置效率驱动，泉州的全要素生产率增长是依靠技术进步驱动。莆田、厦门、三明和宁德的全要素生产率呈现负增长，其中，厦门和莆田的生产率下降是由资源配置效率下降和技术衰退共同导致；三明和宁德的生产率下降是由于技术衰退造成。各地市需要依据自身的发展情况制定改善措施，除泉州外，其他8个城市需要高度重视技术水平的提高，除依靠自主研发外，还应该加强技术引进和技术转化。福州、厦门和泉州作为福建科技创新的中心城市，三地发展并不均衡。福州发展速度最快，但是厦门的科技创新生产率存在退步，而且两地均出现技术退步，要素投入以外的技术进步提升不够，值得警惕；泉州虽然综合技术效率没有变化，但科技进步水平有所提升，引领科技创新的生产前沿。9个城市中，莆田发展滞后，莆田不仅要提升技术水平追赶最优前沿，还要从制度安排、创新环境建设、管理创新等方面着手提升资源配置效率。另外，从区域角度看，福建省四大区域的科技创新全要素生产率均有所提升，但发展不均衡。提升幅度上，闽东>闽南>闽北>闽西。闽东有赖于资源配置效率的大幅改善，科技创新生产率进步最大；闽南和闽北技术水平进展显著，促进生产率显著提升；闽西的科技创新生产率也有提高。政府应该大力促进区域之间的科技交流，各地要抓住创新引领跨越发展的历史性机遇，以科技创新驱动经济增长，缩小地区差异，实现共同发展。

[1]2015全国及各地区科技进步统计监测结果(一)[EB/OL].(2017-09-20).http://www.sts.org.cn/tjbg/tjjc/tcindex.asp.

[2]SUN C H，KALIRAJAN K P. Gauging the sources of growth of high-tech and low-tech industries: the case of korean manufacturing[J]. Australian Economic Papers，2005，44(2)：170-185.

[3]HASHIMOTO A,HANEDA S.Measuring the change in R&D efficiency of the Japanese pharmaceutical Industry[J].Research Policy，2008，37(10)：1829-1836.

[4]GUAN J C，CHEN K H. Modeling macro-R&D production frontier performance：an application to Chinese province-level R&D[J]. Scientometrics，2010，82(1)：165-173.

[5]CLAUDIO，CRUZ C，CRISTINA，et al.You can’t manage right what you can’t measure well：technological innovation efficiency[J].Research Policy，2013，42(6-7)：1239-1250.

[6]HAN U，ASMILA M. Regional R&D efficiency in Korea from static and dynamic perspective[J].Regional Studies，2016，50(7)：1-15.

[7]刘凤朝，潘雄锋.基于Malmquist指数法的我国科技创新效率评价[J].科学学研究,2007, 25(5):986-990.

[8]王珍珍，黄茂兴.我国科技创新效率的实证研究—基于DEA-Malmquist模型和中国省际面板数据[J].技术经济,2013, 32(10):55-61.

[9]刘明广.基于DEA-Malmquist指数法的广东区域创新体系创新效率动态评价[J].统计与管理,2017 (1):67-71.

[10]朱鹏颐，刘东华，黄新焕.动态视角下城市科技创新效率评价研究——以福建九地级市为例[J].科研管理,2017,38(6):43-50.

[11]向小东，林健. 中国工业企业创新全要素生产率评价——基于双前沿面网DEA-Malmquist指数模型[J].工业技术经济,2017,35(9):93-103.

[12]袁博.基于SFA模型的福建创新型企业创新效率分析[J]. 发展研究，2016(3)：68-71.

[13]MALMQUIST S. Index numbers andindifferencecurves[J].Trabajos de Estatistica ,1953(4):209-242.

[14]CAVES D W, Christensen L R, Diewert W E. The economic theory of index numbers and the measurement of input,output,and productivity[J].Econometrica,1982,50(6):1393-1414.

[15]FARER,GROSSKOPF S,NORRISM. Productivitygrowth,technicalProgressand efficiency Changes inindustrializedcountries[J].American EconomicReview,1994, (84):66-83.

[16]BANKER R D,CHARNES A,COOPER W W,et al. An introduction to data envelopment analysis with some of its models and their users[J].Research in Government and nonprofit Accounting, 1989(5): 125-163.

[17]COE S M HELPMAN. International R&D spillovers[J]. European Economic Review, 1995, 39(5):859-887.

[18]朱有为，徐康宁.中国高技术产业研发效率的实证研究[J]. 中国工业经济，2006(11)：38-45.

[19]吴延兵. 用DEA方法评测知识生产中的技术效率与技术进步[J].数量经济技术经济研究,2008(7):67-79.

[20]赖明勇，王文妮.全要素生产率和经济增长方式——基于1952—2006年的Malmquist指数分析[J].求索,2008 (11):3-8.