利用EGM2008模型与加权组合模型进行高程异常拟合

罗陶荣，王中元，梁 宁，马效申

(1. 中国矿业大学环境与测绘学院， 江苏 徐州 221116； 2. 绍兴市城市规划测绘院，浙江 绍兴312000)

高程异常拟合是GPS高程测量应用于实际工作的重要技术手段，高精度地求解高程异常是技术关键。对于这一热点问题，国内外学者进行了大量的研究探索，目前主要的方法有数学模型拟合法、利用地球重力场模型求高程异常和神经网络方法。这些方法各有优点，但是对应用的地形和分布情况有一定要求，不能满足复杂的环境。

针对这一问题，国内外学者进行了大量的研究探索。邢志斌等[1]提出了快速构建利用垂线偏差计算高程异常差法方程的方法，使高程异常差计算更加高效；刘斌等[2]提出了利用EGM2008重力场模型和地形改正进行高程异常计算的方法，该方法能够达到较高的精度但是不能适应较为复杂的应用环境；黎剑[3]提出了一种加权综合模型高程异常拟合方法，该方法兼顾多种方法的优势具有良好的适应性，但是没有引入EGM2008重力场模型进行改正导致高程异常拟合精度不高。

本文提出一种顾及EGM2008重力场模型的加权组合模型高程异常拟合方法，该方法具有较高的拟合精度并且能够适应较为复杂的应用环境。通过实际数据验证可知，该方法的解算精度能够达到厘米级，使程异常拟合的效果提升10%～30%。

1 原理与方法

1.1 原理与流程

本文通过“移去—恢复”法求解高程异常，该方法可以根据EGM2008重力场模型和联测少量水准点对GPS高程异常进行拟合而不需要测量额外的重力参数，能够适应地形起伏较大且水准联测点较少的区域，具有高效率和较好的适用性。根据物理大地测量学理论，可以得出GPS高程拟合的表达式[4]为

ζ=ζGM+ζCT+ζRES

(1)

式中，ζGM是由EGM2008重力场模型求得的高程异常长波项；ζRES是残余高程异常，为高程异常的中波项；ζCT是通过地形改正解算获得的高程异常短波项。本文引入EGM2008重力场模型来求解高程异常中的长波项，对于其中的短波项和中波项通过加权组合模型进行求解。故将式(1)变换成[5]

ζ=ζGM+ζ0

(2)

式中，ζ0表示高程异常的短波项和中波项，统称残余高程异常值。“移去—恢复”法的核心思想为，将已知点高程异常中通过EGM2008重力场模型求解的长波项ζGM移去，剩下残余高程异常值ζ0运用加权组合模型对其进行拟合；通过加权组合模型对未知点的残余高程异常ζ0进行求解，再加上高程异常长波项ζGM就可以得到未知点的高程异常ζ。具体的解算流程如图1所示。

图1 “移去—恢复”法

1.2 EGM2008重力场模型求解高程异常长波项

EGM2008全球重力场模型是由美国国家地理空间情报局，通过先进建模技术与算法，结合测高数据和重力数据，得到拓展至2190次球谐系数的全球超高阶地球重力场模型。EGM2008全球重力场模型的覆盖率高达83.8%，模型分辨率达到5′，全球5′×5′网格的估算精度最小误差为0.304 5 dm，平均误差为1.114 dm。

利用EGM2008重力场模型求解地球上任意一点的GPS高程异常长波项ζGM，首先要计算重力扰动位，再根据Burns公式计算ζGM。Burns[4]公式如下

(3)

1.3 加权组合模型

本文根据黎剑的加权综合模型提出了一种权重动态变化的加权组合模型，该模型能够根据两种高程拟合方法的拟合效果动态确定两种方法的权重，具有更好的拟合精度和计算效率。本文选用二次曲面拟合方法与多面函数拟合方法作为组合模型的基本拟合单元，动态分配两种拟合单元的权重，最后得到加权后的GPS高程异常模型，如图2所示。

图2 加权组合模型算法

二次曲面拟合方法的公式为[6]

ξ(x,y)=a0+a1Δx+a2Δy+a3Δx2+a4Δy2+a5ΔxΔy

(4)

式中，ai(i=0,1,2,…,5)为二次曲面拟合模型的系数；Δx=x-x0；Δy=y-y0；(x0，y0)一般为重心点坐标。

多面函数拟合方法的公式为[7-8]

(5)

式中，aj(j=1,2,3,…,n)为各个核函数的比例系数，是需要求取的关键参数；Q(x,y,xj,yj)为核函数。本文选用了对称性较好的正双曲面函数作为核函数[8]

(6)

式中，δ为光滑系数，系数的取值根据实际情况而定，也就是说若想获得一个测区的最佳多面函数模型就需要对δ的取值作出准确判断，通常是取一系列数据分析模型精度选取最佳光滑系数值。本文取多面函数模型的光滑系数δ=5。

加权组合模型的公式为[3]

(7)

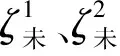
2 算例分析

2.1 试验区及试验分组介绍

本文以江苏省某市C级GPS测量成果和一等水准测量成果为研究数据对提出的高程拟合新方法进行实际数据的验证。该试验区长21 km，宽20 km，点位均匀分布，具体分布如图3所示。由图3可知，共有30个已知点，其中25个作为已知点(三角形表示)，最大高程为481.810 0 m，最小高程为260.915 8 m，平均高程为372.785 0 m；5个作为检核点(圆形表示)，最大高程为448.320 3 m，最小高程为75.327 7 m，平均高程为222.848 4 m。高程异常曲面如图4所示。

试验区内的高程点的坐标值、高程异常值(ζ)、高程异常长波项(ζGM)及残余高程异常值(ζRES)见表1。

图3 点位分布

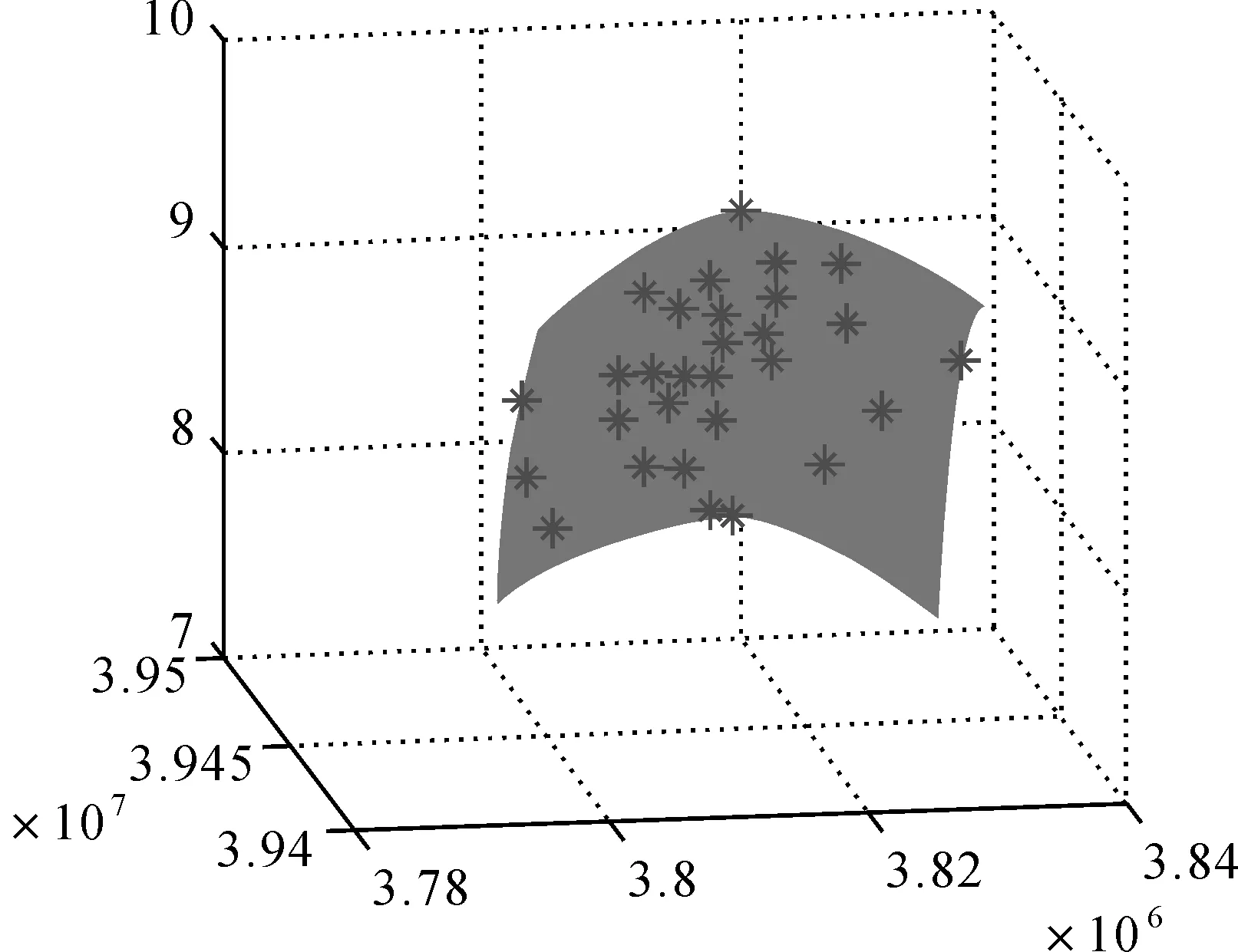
图4 高程异常曲面

点号纬度(B)/(° ′ ″)经度(L)/(° ′ ″)高程异常(ζ)/m高程异常长波项(ζGM)/m残余高程异常(ζRES)/m1334．280473683116．2126554108．9989．257-0．2592034．243935403116．2539383018．6248．939-0．3152234．261696960116．2346416808．7879．105-0．3182434．262193619116．1907406089．1489．386-0．2382634．282952237116．1843342529．2089．43-0．222

本文采用未顾及EGM2008重力场模型的二次曲面拟合方法、多面函数拟合方法及其加权组合模型对试验区内的数据进行GPS高程拟合，然后采用顾及EGM2008重力场模型的二次曲面拟合方法、多面函数拟合方法及其加权组合模型对试验区内的数据进行GPS高程拟合。具体试验模型和方法选择及其分组编号见表2。

表2 试验模型与方法组合及其编号

2.2 试验结果及分析

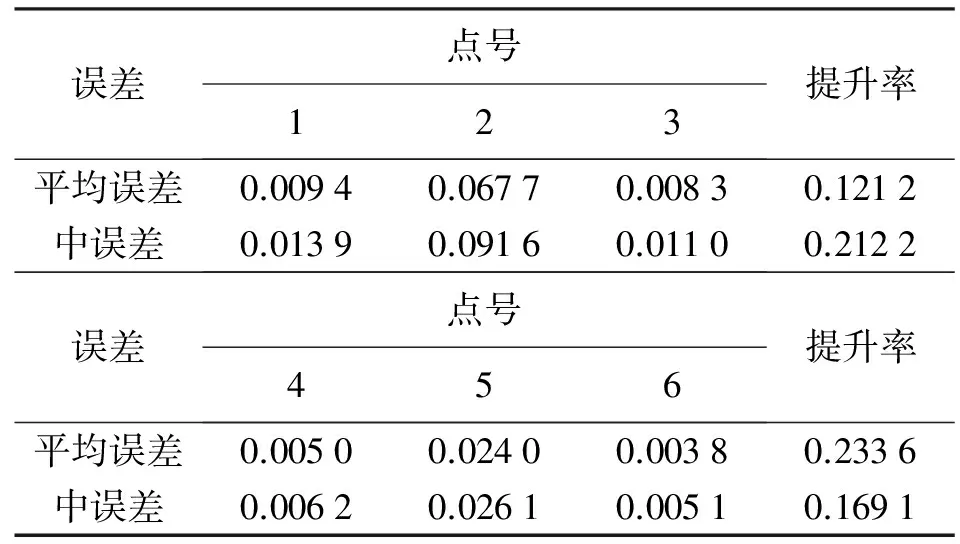
本文根据间接平差原理进行算法设计并实现，通过算法对6种组合试验进行验证，计算得到高程残差值见表3。

由表3可知，高程异常拟合的精度达到了厘米级，满足GPS定位对于高程的要求。未顾及EGM2008重力场模型时3种方法拟合的精度：二次曲面拟合方法拟合结果中误差1.39 cm，平均残差0.94 cm；多面函数拟合方法拟合结果中误差9.16 cm，平均残差6.77 cm；加权组合模型拟合方法拟合结果中误差1.1 cm，平均残差0.83 cm。顾及EGM2008重力场模型时3种方法拟合的精度：二次曲面拟合方法拟合结果中误差0.62 cm，平均残差0.5 cm；多面函数拟合方法拟合结果中误差2.61 cm，平均残差2.4 cm；加权组合模型拟合方法拟合结果中误差0.51 cm，平均残差0.38 cm。

表3 验证点高程异常拟合残差 m

顾及EGM2008重力场模型时3种拟合方法的拟合精度明显好于未顾及EGM2008重力场模型时3种拟合方法的拟合精度，通过引入EGM2008重力场模型能够有效提高高程异常的拟合精度。顾及EGM2008重力场模型和未顾及EGM2008重力场模型的拟合效果如图5所示。

图5 EGM2008重力场模型对高程拟合的影响

由图5可知，在顾及EGM2008重力场模型时二次曲面拟合法和加权组合模型拟合法的高程异常拟合残差整体要小于未顾及EGM2008重力场模型时高程异常拟合残差，且高程异常残差的离散程度也较小；多面函数拟合方法的高程异常拟合残差整体要大于未顾及EGM2008重力场模型时高程异常拟合残差，且高程异常残差相近。由图6可知，加权组合模型拟合效果在顾及EGM2008重力场模型和未顾及EGM2008重力场模型时都优于二次曲面拟合方法和多面函数拟合方法。

图6 加权组合模型对高程拟合的影响

m

注：提升率ρ=(α-β)/α，α为二次曲面法与多面函数法中最高精度，β为加权组合模型精度。

由表4可知，加权组合模型拟合效果整体可以提升10%～30%，具有很好的拟合效果和实际意义。

2.3 工程实例

将本方法应用于广东某市城市测量工程中，通过已知高程点的水准高程和GPS高程，对测区内的高程点进行高程拟合计算。计算结果见表5。分析可知，加权组合模型方法达到GPS高程测量精度水准，满足GPS高程的要求并且具有较好的实用性。

表5 应用实例数据 m

3 结 语

通过引入EGM2008重力场模型能够计算高程异常长波项的值，在高程异常拟合计算中可以移出高程异常长波项的值，从而提高高程异常拟合的精度。加权组合模型可以兼顾二次曲面拟合方法和多面函数拟合方法的优点，既能保证高程异常整体的平滑又能顾及高程异常极小误差，保证高程异常结果精度。顾及EGM2008重力场模型的加权组合模型拟合方法能够显著提升高程异常拟合的精度，拟合效果可以提升10%～30%。工程实例的应用说明，加权组合模型能够满足GPS高程测量精度要求，具有较好的实用性。

[1] 邢志斌，李姗姗，王伟，等.利用垂线偏差计算高程异常差法方程的快速构建方法[J].武汉大学学报(信息科学版)，2016，41(6)：778-783.

[2] 刘斌，郭际明，史俊波，等.利用EGM2008模型与地形改正进行GPS高程拟合[J].武汉大学学报(信息科学版)，2016，41(4)：554-558.

[3] 黎剑.区域GPS高程异常拟合及建模方法研究[D].昆明：昆明理工大学，2013.

[4] ITOH S，YASUDA I.Characteristics of Mesoscale Eddies in the Kuroshio-Oyashio Extension Region Detected from the Distribution of the Sea Surface Height Anomaly[J].Journal of Physical Oceanography，2010，40(5):1018-1034.

[5] SREEJITH K M，RAJESH S，MAJUMDAR T J，et al.High-resolution Residual Geoid and Gravity Anomaly Data of the Northern Indian Ocean——An Input to Geological Understanding[J].Journal of Asian Earth Sciences，2013，62(62):616-626.

[6] LI Feng，ZHOU X，LI Xin，et al.The Application of Ridge Estimation in GPS Height Fitting with Polynomial Surface[J].Coastal Engineering，2012.

[7] XU N，YAN Z，MA F.Multi-surface Function Model of GPS Height Fitting Based on Genetic Algorithm[J].Geotechnical Investigation & Surveying，2013.

[8] WU Y，ZHU J，ZUO T.The Application of Vondrak Filter Combined with Multisurface Function in Height Anomaly Fitting[J].Gohnal Nvgaon & Rvyng，2012，40(7):58-61.

[9] 高伟，徐绍铨.GPS高程分区拟合转换正常高的研究[J].武汉大学学报(信息科学版)，2004，29(10)：908-911.

[10] 何海清，黄声享，陈婷.一种顾及粗差的径向神经网络高程曲面拟合法[J].武汉大学学报(信息科学版)，2015，40(4):547-551.

[11] 唐健林，徐陶，龙盈.小波函数应用于GPS高程拟合的分析[J].测绘通报，2016(3)：58-60.DOI:10.13474/j.cnki.11 -2246.2016.0086.

[12] 田晓，郑洪艳，许明元，等.一种改进的适用于不同地形的GPS高程拟合模型[J].测绘通报，2017(1):35-38.DOI:10.13474/j.cnki.11-2246.2017.0008.

[13] 周长志，孙佳龙，郭淑艳.基于移动-多面函数高程异常拟合方法[J].测绘通报，2016 (12)：25-27.DOI:10.13474/j.cnki.11-2246.2016.0394.

[14] 陈艳红，马全明，刘瑞敏，等.基于相对高程异常的GPS高程拟合方法探讨[J].测绘通报,2014(12):67-69.

[15] 肖杰，张锦，邓增兵，等.矿区似大地水准面精化方法研究[J].测绘通报,2015(2):14-18.DOI:10.13474/j.cnki.11-2246.2015.0032.

[16] 赫林，李建成.褚永海.1985国家高程基准与全球高程基准之间的垂直偏差[J].测绘学报，2016，45(7):768-774.DOI:10.11947/j.AGCS.2016.20160029.