利用GRACE数据检测日本Mw9.0地震同震和震后重力变化

尹 鹏，张永志，焦佳爽，南康康，王慧玲

(长安大学地质工程与测绘学院，陕西 西安 710054)

2011年3月11日在日本东北海域发生Mw9.0级地震，此次地震发生在太平洋板块和欧亚板块的边界上。根据美国地质勘查局(USGS)发布的地震监测信息，该地震的震中位于东经142.4°、北纬38.3°的日本海沟底部。

强震的孕育和发生必然引起震源区和外围地区一定范围内地球重力场的变化。Sun & Okubo[1]提出大于Mw9.0的剪切型或大于Mw7.5的张裂型地震所产生的重力变化可以被GRACE观测到，并得到证实[2-7]。2011年日本Mw9.0地震发生后，Matsuo & Heki[8]利用地震后两个月的GRACE数据检测到了-7 μgal重力负变化，同时发现GRACE检测到的大地震重力负变化幅度与地震矩的大小存在近似线性关系；邹正波等[9]采用不同的时间尺度，详细分析研究了地震发生前后的重力动态演化过程，反映出该区域的物质运动和质量迁移；张克亮等[10]采用最小二乘法和经验正交函数方法，提取了日本Mw9.0地震震区及其周边的同震变化特征，但未考虑陆地水储量变化的影响，并且缺乏断层模型正演结果的检验。

前人已利用GRACE数据对日本地震同震和震后重力变化进行研究，但震后数据的时段不长，考虑到数据长度及陆地水储量的变化在同震和震后研究的重要性，本文利用GRACE数据，扣除陆地水储量的影响，结合位错模型正演的同震重力变化，计算日本Mw9.0地震震中及其周边地区的同震和震后5 a的重力场演化过程。

1 数据选取

1.1 GRACE卫星月重力场模型数据

德国地学中心(GFZ)发布的RL05月重力场模型给出完全正则化的球谐系数，在解算过程中已经扣除固体潮、极潮、大气、海洋等因素的影响。该模型的最高阶次为90阶，大于60阶的数据会引入较大的误差，故将球谐系数截断至60阶[11]，选取2009年3月至2016年3月的重力场模型进行分析，由于GRACE卫星进入生命末期，存在数据缺失情况，同时地震发生时段(2011年3月)的数据也一并舍去不用。由于GRACE卫星对于低阶项不敏感，采用人工激光测距得到的二阶项代替球谐系数中的C20项。

1.2 GLDAS陆地水数据

GLDAS(global land data assimilation system)是美国国家航空航天局(NASA)戈达德空间飞行中心(GSFC)发布的陆地水储量模型。GLDAS陆地水储量包括土壤水分和雪水变化，最大时间分辨率为3 h，最大空间分辨率为0.25°×0.25°。GRACE观测的重力变化包含多种信号共同作用，土壤水分和雪水变化是除地震外最重要的影响因素[8]，本文选取1°×1°的月水储量模型，提取陆地水含量引起的重力变化，并将其从GRACE月重力场模型中扣除，去除这一非构造因素对同震和震后重力变化的影响。

2 重力信号提取

2.1 GRACE数据处理

由于GRACE卫星观测本身的限制及解算中采用的大气和海洋等模型误差因素的影响，GRACE时变重力场在图像上表现出明显的“南北条带”误差，本文采用300 km的扇形滤波处理条带误差，加入扇形滤波后椭球面上的GRACE时变重力变化可表达为[12]

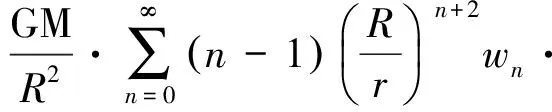
(1)

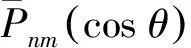
提取同震重力变化信号时，为了削弱时变重力场的季节性影响，突出同震重力变化，选取日本Mw9.0地震前2009-11—2010-02、2010-11—2011-02的平均重力场为背景场，利用震后两年相同月份的平均重力场与背景场差分，其中2011-01数据缺失，为了保证数据的对称性，舍去2010年1月的数据。提取震后重力演化信号时，利用震后每年相同月份的平均重力场与背景重力场进行差分，其中2014-02、2014-12、2015-11数据缺失，分别用2014—2016年1月的数据代替。

2.2 GLDAS数据处理

球面上的任意函数f(θ,λ)可以展开为球谐级数[13]，由此可将土壤水分和雪水含量转化为与之对应的球谐系数[14]

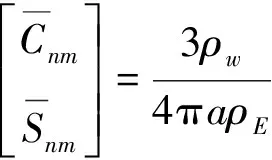
(2)

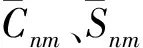
选取与GRACE数据相同月份的GLDAS数据计算陆地水储量对同震重力的影响，如图1所示，图中黑色五角星表示震中。图1(a)为日本地震震中周围地区震后2年与震前2年1°×1°的平均等效水高之差，主要为负值。在黑龙江东部的中俄交界处、俄罗斯滨海边疆区南部及日本本州东北部等地有比较明显的水文效应，俄罗斯滨海边疆区南部的等效水高之差正负值均达到最大，分别为-115.2和59.8 mm；在日本的北海道、本州西南部、四国及九州地区的水文效应为正值，日本本州东北部和北海道的最大等效水高分别为-44.3、23.2 mm。

将地震前后的等效水高按式(2)转化为球谐系数，为了达到和GRACE一致的空间分辨率，将展开后的球谐系数截断至60阶，并加以300 km的扇形滤波，获得地震前后两年1°×1°的等效水高之差，如图1(b)所示。空间平滑后，部分陆地信号泄露到海洋地区，空间分辨率降低，等效水高振幅减小，由原来的-115.2 mm～59.8 mm，降至-8.5 mm～1.6 mm，在俄罗斯滨海边疆区南部、日本本州东北部的负水文效应比较显著，分别为-8.5和-4.2 mm，与图1(a)的负水文效应空间对应关系较好；本州东南呈现正的水文效应，最大值为1.6 mm。

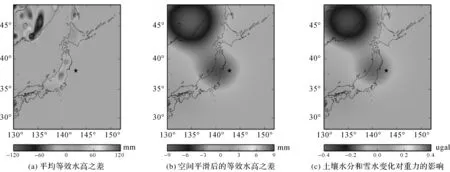
图1 日本Mw9.0地震前后2年土壤水分和雪水变化及其引起的重力变化

将式(2)得到的球谐系数截断为60阶后代入式(1)，即可求得土壤水分和雪水变化引起的重力变化，如图1(c)所示，在空间分布上与图1(b)基本对应，空间平滑后，9 mm的等效水高变化大致与0.4 μgal的重力变化相对应。总体上看，土壤水含量和雪水的变化引起的重力变化约为-0.34～0.09 μgal。

2.3 同震和震后重力变化

按照前文所述方法，在不考虑陆地水储量效应时获得的日本Mw9.0地震震中周围地区的同震重力变化，如图2(a)所示，黑色五角星代表震中，黑色方框为Wei给出的断层模型边界[15]。由提取的重力信号可知，在断层破裂面两侧重力呈正-负变化分布，量值范围在-5.4～4.1 μgal，震中北方向出现了以(140.8°E，45.4°N)为中心，量值最高达3.7 μgal的正重力异常极值区。

图2(b)所示为扣除土壤水分和雪水影响之后重力变化的空间分布，重力变化幅度为-5.3～4.2 μgal，北海道北部(140.8°E，45.4°N)的正重力异常极大值仍然有3.9 μgal，由于采用叠积法计算的同震重力变化包含震后重力变化信息，此处出现的重力异常可能与震后壳幔物质调整有关[6]。图2(b)在空间分布上与图2(a)基本一致，但有细微差别，北海道附近的重力极大值区扩张，日本本州西部日本海域的负极值区收缩，虽然水文效应对日本Mw9.0地震同震重力的影响不明显，但在汶川Ms8.0地震[16]、尼泊尔M8.1地震[17]等同震重力变化较小的情况下，提取同震重力变化信号需要考虑水文效应的影响。

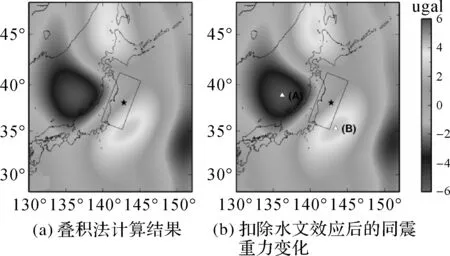
图2 日本Mw9.0地震的同震重力变化

图3所示为日本Mw9.0地震震后重力时空演化过程，均扣除了土壤水分和雪水的影响。(a)—(e)分别为震后1～5 a相对于背景重力场的重力变化量，日本Mw9.0地震震后震中及其周边地区的重力变化基本与同震重力变化特征基本一致，震后5 a重力整体上呈增加趋势，断层上盘所在的日本海域重力增加的最大值为2.6 μgal，断层下盘所在的太平洋区域重力增加较明显，重力增加的峰值为4.5 μgal，比同震重力变化大0.3 μgal。

2.4 特征点时序重力变化

为了反映震后重力的详细变化过程，在断层上下盘各取一个重力变化极值点A(136.2°E，38.9°N)、B(143.4°E，35.3°N)，如图2(b)中所示的白色三角形。以2009-03—2011-02共23个月(2011-01数据缺失)的GRACE数据均值为背景场，分别计算2009-03—2016-03各月重力场相对于背景场的差值，并加以300 km的扇形滤波，对于缺失月份的重力场数据，取其前后月重力场模型的均值来代替，获取A、B两点相对于背景场的月重力变化时间序列并采用最小二乘拟合的方法扣除时序重力变化中周期性水文及S2潮汐波的影响[18]

(3)

式中，A为常数项；B为年变率；Δt为相对参考历元的时间差；wi为振幅Ci和Di的周期项角频率；i=1,2,3分别表示周年、半周年项及与S2潮汐波相关的161 d混频项；ε为残差。

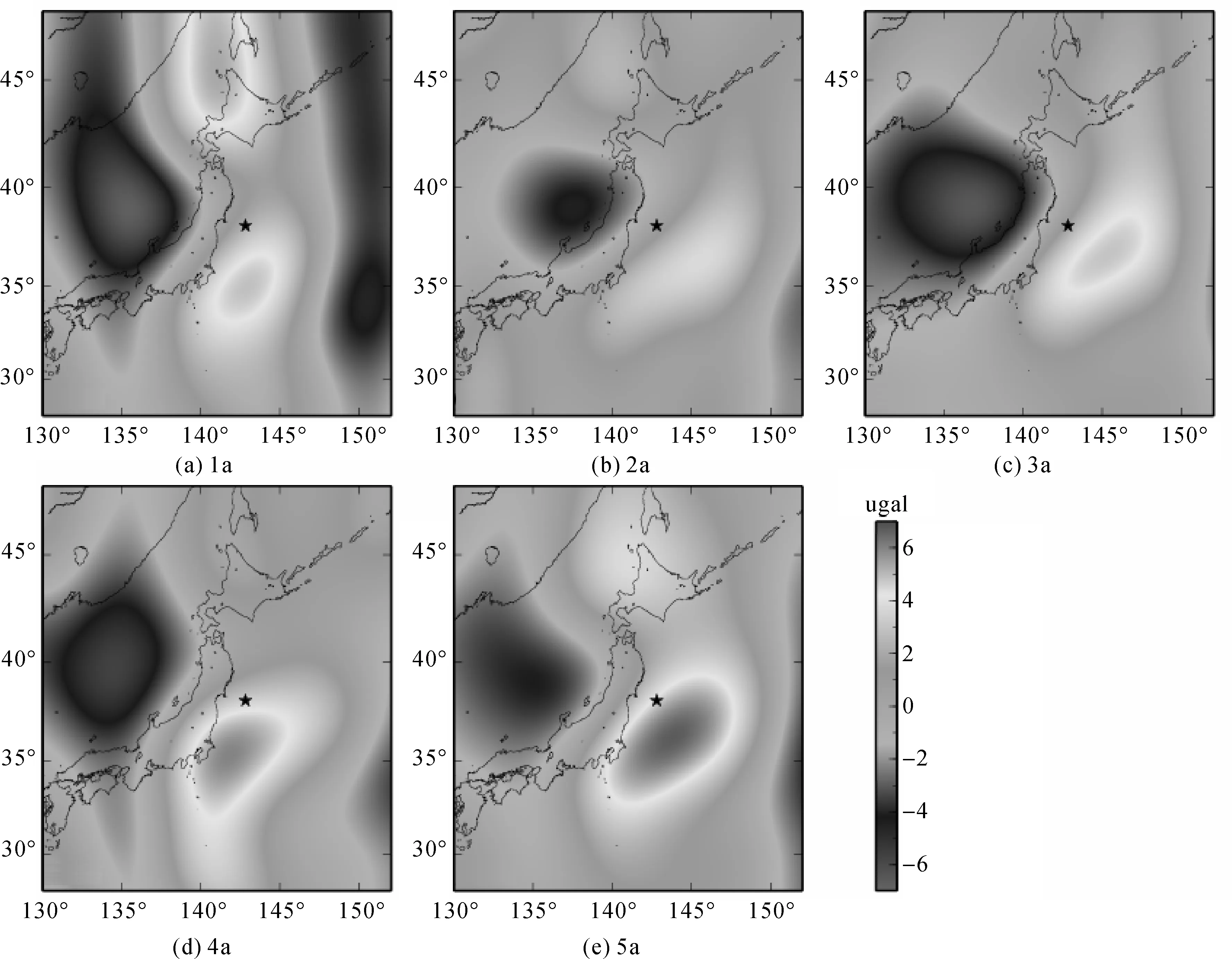
图3 日本Mw9.0地震震后重力演化过程

图4(a)、(b)分别表示A、B点的月时序重力变化，方块曲线表示仅进行扇形滤波的时间序列，圆圈曲线表示最小二乘拟合的时间序列，黑色虚线表示地震发生的2011年3月，黑色五角星表示地震发生当月的重力场与背景重力场的差值，黑色实线表示地震前后扣除周期性信号之后重力的线性变化趋势。由图4可以看出，A、B两点都有明显的同震阶跃，A、B两点的年变率见表1，震前A点重力增加，B点基本保持不变；震后均呈增加趋势，B点的重力年变率为0.77 μgal/a，重力增加较A快，可能是因为B点所在的太平洋地层黏滞性相对较低。

表1 日本Mw9.0地震前后A、B两点重力的年变率

3 日本Mw9.0地震理论同震重力变化

为验证GRACE卫星测得同震信号的可靠性，采用分层黏弹性半空间位错模型PSGRN/PSCMP[19]及Wei发布的断层模型[15]计算2011年日本Mw9.0地震的同震重力变化，计算过程中采用5层分布的地球模型，见表2。PSGRN/PSCMP位错模型计算的是变形地表的重力变化，与地面重力测量结果对应，为了与GRACE卫星的空间观测结果保持一致，需要在位错模型计算结果的基础上加入地表垂直形变引起的空间改正[20]，由于此次地震发生在海域，还需加入海水质量改正[21],将改正后的结果加以300 km的扇形滤波，以达到和GRACE一致的空间分辨率。理论同震重力变化空间分布如图5所示。

图4 日本Mw9.0地震前后A、B两点的时序重力变化

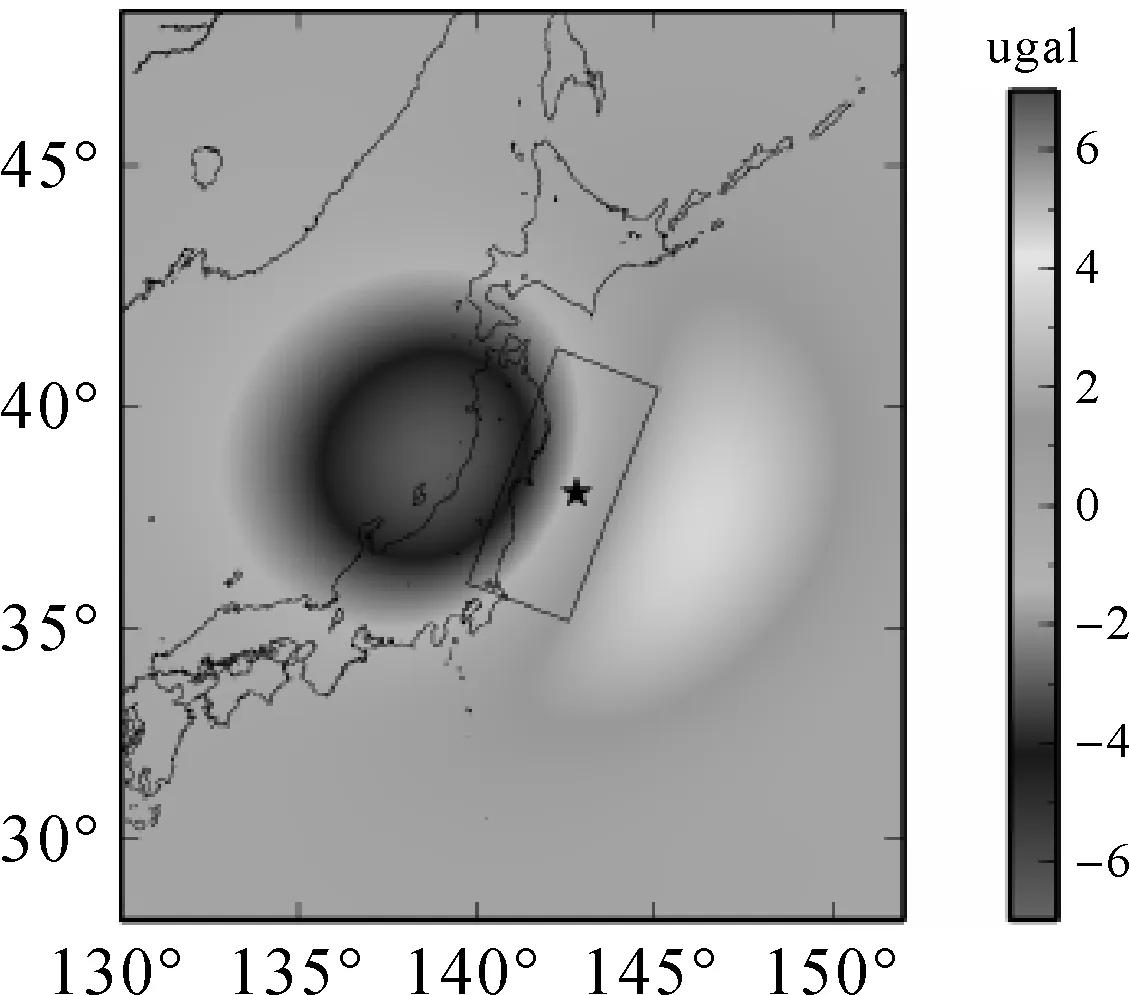
图5 日本Mw9.0地震理论同震重力变化

由图5可知，理论同震重力变化与利用GRACE重力场模型计算的同震重力变化在量级和空间分布上具有较好的一致性。断层上盘的负重力异常，理论结果为-6.6 μgal，GRACE卫星观测结果为-5.3 μgal；断层下盘的正重力异常，理论结果为3.7 μgal，GRACE卫星观测结果为4.2 μgal。理论重力变化与GRACE观测结果存在的差别可能是因为叠积法计算的同震重力变化中包含震后重力变化，同震和震后信号未分离。

4 结 语

日本Mw9.0地震前后两年，震中及周边地区土壤水分和雪水的平均等效水高变化为-8.5～1.6 mm，引起的重力变化为-0.34～0.09 μgal，9 mm的等效水高变化与0.4 μgal的重力变化相对应，虽然水文效引起的重力变化较小，但扣除水文效应能更准确地反映同震重力变化。扣除水文效应的影响之后，同震重力变化的幅度为-5.3～4.2 μgal，PSGRN/PSCMP模型计算的同震重力变化为-6.6～3.7 μgal，二者在空间分布上的对应关系比较好，在数值上存在细微差别的原因是没有将震后重力变化与同震重力变化分离。

表2日本Mw9.0地震5层分布的地球模型(各层参数来自于CRUST1.0)

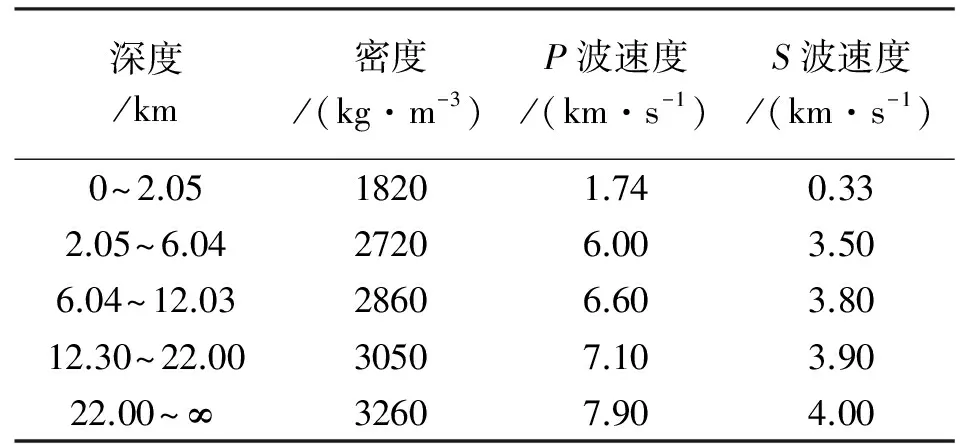
深度/km密度/(kg·m-3)P波速度/(km·s-1)S波速度/(km·s-1)0～2．0518201．740．332．05～6．0427206．003．506．04～12．0328606．603．8012．30～22．0030507．103．9022．00～∞32607．904．00

震后重力变化与同震重力变化特征基本保持一致，震后5 a震中附近区域的重力整体上呈现增加趋势，断层上盘所在的日本海域重力增加的最大值为2.6 μgal，下盘所在的太平洋区域重力增加的最大值为4.5 μgal，比同震重力大0.3 μgal，可能与断层下盘所在地层的黏滞性相对较低有关。利用最小二乘拟合的方法计算了两特征点在地震前后85个月的重力年变率，震后两个特征点的重力年变率分别为0.19与0.77 μgal/a，重力变化均呈现增加趋势。

在利用叠积法计算日本Mw9.0地震同震和震后重力变化时，采用了300 km的扇形滤波，较好地消除了南北条带误差，但仍然存在不太明显的条带，可以尝试去相关滤波和扇形滤波相结合的方法。

[1] SUN W，OKUBO S.Coseismic Deformations Detectable by Satellite Gravity Missions：A Case Study of Alaska(1964，2002)and Hokkaido(2003)Earthquakes in the Spectral Domain[J].Journal of Geophysical Research Solid Earth，2004，109(B4):327-341.

[2] HAN S C，SHUM C K，BEVIS M，et al.Crustal Dilatation Observed by GRACE after the 2004 Sumatra-Andaman Earthquake[J].Science，2006，313(5787):658.

[3] CHEN J L，WILSON C R，TAPLEY B D，et al.GRACE Detects Coseismic and Postseismic Deformation from the Sumatra-Andaman Earthquake[J].Geophysical Research Letters，2007，34(13):173-180.

[4] RYOKO O，KOSUKE H.Slow Postseismic Recovery of Geoid Depression Formed by the 2004 Sumatra-Andaman Earthquake by Mantle Water Diffusion[J].Geophysical Research Letters，2007，34(6):160-166.

[5] ISABELLE P，VALENTIN M，MICHEL D，et al.Coseismic and Post-Seismic Signatures of the Sumatra 2004 December and 2005 March Earthquakes in GRACE Satellite Gravity[J].Geophysical Journal of the Royal Astronomical Society，2007，171(1):177-190.

[6] DE LINAGE C，RIVERA L，HINDERER J，et al.Separation of Coseismic and Postseismic Gravity Changes for the 2004 Sumatra-Andaman Earthquake from 4.6 yr of GRACE Observations and Modelling of the Coseismic Change by Normal-Modes Summation[J].Translated World Seismology，2010，176(3):695-714.

[7] 周新，孙文科，付广裕.重力卫星GRACE检测出2010年智利Mw8.8地震的同震重力变化[J].地球物理学报，2011，54(7):1745-1749.

[8] KOJI M，KOSUKE H.Coseismic Gravity Changes of the 2011 Tohoku-Oki Earthquake from Satellite Gravimetry[J].Geophysical Research Letters，2011，38(7):113-120.

[9] 邹正波，罗志才，吴海波,等.日本MW9.0地震前GRACE卫星重力变化[J].测绘学报，2012，41(2):171-176.

[10] 张克亮，甘卫军，周新.GRACE卫星重力场同震变化的经验正交函数分解:以日本MW9.0地震为例[J].地震地质，2014，36(3):763-774.

[11] CHEN J L，RODELL M，WILSON C R，et al.Low Degree Spherical Harmonic Influences on Gravity Recovery and Climate Experiment (GRACE) Water Storage Estimates[J].Geophysical Research Letters，2005，32(14):57-76.

[12] ZHANG Z，CHAO B F，YANG L，et al.An Effective Filtering for GRACE Time-Variable Gravity：Fan Filter[J].Geophysical Research Letters，2009，36(17):1397-1413.

[13] HEISKANEN W A，MORITZ H.Physical Geodesy[J].Bulletin Géodésique (1946-1975)，1967，86(1):491-492.

[14] WAHR J，MOLENAAR M，BRYAN F.Time Variability of the Earth’s Gravity Field：Hydrological and Oceanic Effects and Their Possible Detection Using GRACE[J].Journal of Geophysical Research Solid Earth，1998，103(B12):30205-30230.

[15] WEI S，SLADEN A，ARIA group. Updated Result[EB/OL].2011-11-03. http:∥www.tectonics.caltech.edu/slip_history/2011_taiheiyo-oki/.

[16] 李进.基于GRACE时变重力梯度探测大地震的同震变化[D].武汉：武汉大学，2011.

[17] 邹正波，李辉，吴云龙,等.尼泊尔M8.1地震震前卫星重力场时变特征[J].大地测量与地球动力学，2015，35(4):547-551.

[18] STEFFEN H，GITLEIN O，DENKER H，et al.Present Rate of Uplift in Fennoscandia from GRACE and Absolute Gravimetry[J].Tectonophysics，2009，474(1-2):69-77.

[19] WANG R，MARTN F，ROTH F.PSGRN/PSCMP—A New Code for Calculating Co- and Post-seismic Deformation，Geoid and Gravity Changes Based on the Viscoelastic-Gravitational Dislocation Theory[J].Computers & Geosciences，2006，32(4):527-541.

[20] SUN W，OKUBO S，FU G，et al.General Formulations of Global Co-seismic Deformations Caused by an Arbitrary Dislocation in a Spherically Symmetric Earth Model-Applicable to Deformed Earth Surface and Space-fixed Point[J].Geophysical Journal International，2009，177(3):817-833.

[21] HEKI K，MATSUO K.Coseismic Gravity Changes of the 2010 Earthquake in Central Chile from Satellite Gravimetry[J].Geophysical Research Letters，2010，37(24):701-719.