微小卫星三轴磁强计测量误差校正方法

刘燎 孙华苗 何波 薛力军 张迎春，3

(1 深圳航天东方红海特卫星有限公司，广东深圳 518064)(2 微小卫星控制系统仿真与测试工程实验室，广东深圳 518064)(3 哈尔滨工业大学航天学院，哈尔滨 150001)

三轴磁强计能用来测量载体所处周边环境的磁场强度大小和方向。在传统航天器中，采用宇航级的三轴磁强计，其测量精度较高，稳定性较好，在各种恶劣环境和复杂条件下具有良好的适应性，能够满足中低轨道航天器基本任务需求，目前已广泛应用于航天器姿态确定与控制。近年来，随着微小卫星的发展，传统的宇航级三轴磁强计已不能满足微小卫星成本低、质量小等要求，越来越多的低成本(商用/工业级)三轴磁强计逐步应用到微小卫星的姿态确定与控制系统中[1]。低成本三轴磁强计能够满足一般微小卫星低轨低精度姿态确定的要求，具有价格低、质量小、体积小、可靠性高等优点，但具有稳定性较差、对环境适应性差的缺点。例如，温度漂移系数的差异使不同温度下的低成本三轴磁强计的测量精度大大降低(最大为几千纳特)，导致姿态确定误差可达几度，大大降低了姿态确定精度。因而，如何对低成本三轴磁强计的测量误差进行校正，成为磁强计应用中的一个研究重点。

在三轴磁强计实际工作时，地磁信号和各类误差信号耦合在一起，由传感器输出，这将严重影响三轴磁强计的测量精度。目前，三轴磁强计测量误差的校正方法主要有：采用椭球曲面拟合三轴磁场强度数据，利用递推法计算标定参数[2]；从三轴磁强计测量误差来源进行分析和建模，建立三轴磁强计校正模型[3]；采用基于总体最小二乘算法对模型的参数进行估计[4]；基于遗传算法融合的最小二乘算法对三轴磁强计进行标定校准[5]；利用三轴磁强计和计算磁场强度的在轨数据通过非线性最小二乘算法对三轴磁强计进行标定[6-7]；基于粒子群算法(PSO)的三轴磁强计标定参数估计[8]；基于扩展卡尔曼滤波方法对三轴磁强计进行在轨实时校准[9]；基于改进最小二乘估计器的三轴磁强计校正方法[10]；此外，文献[11]中对三轴磁强计的在轨标定及测量应用进行了说明。以上标定方法，或者是针对宇航级磁强计，温漂系数很小，或者是在地面进行标定，温度变化小，即使没有考虑温度的影响，也能达到良好的标定效果。由于微小卫星采用的三轴磁强计存在温度漂移，因而会导致三轴磁强计测量的零位误差、标度系数误差和非正交误差等不是固定值，可能随着温度变化，在温度变化几十度范围内会导致上千纳特的测量误差。

本文针对三轴磁强计的测量误差进行分析，对三轴磁强计的校正原理进行数学建模，并基于该模型在温度可变的磁环境模拟器中对三轴磁强计进行测试，验证了本文方法的实用性。

1 三轴磁强计测量误差校正模型

三轴磁强计的测量误差主要由零偏误差、标度系数误差及三轴垂直度误差组成。零偏误差是指三轴磁强计在使用过程中内部剩磁及电路漂移等导致的传感器输出漂移。标度系数误差是指组成三轴磁强计的3个传感器电气特性不完全对称，导致其标度系数不同而造成的误差。三轴垂直度误差是指三轴磁强计的3个轴不完全正交带来的误差。本文首先根据三轴磁强计的测量误差建立三轴磁强计的误差校正模型，通过磁场强度的梯度变化得到线性方程组。为了在全温度范围内对三轴磁强计进行标定，在不同温度下分别利用伪逆法计算标定系数。最后，在全温度范围内对不同温度下的零位电压和标定系数进行温度的线性拟合，得到满足全温度范围内的零位电压和标定系数，从而实现对由于温度引起的零位电压误差、标度系数误差和非正交误差的校正。

1.1 数学建模

一般，三轴磁强计在卫星上安装时，会使其机械坐标系和卫星本体坐标系(OXbYbZb)的3个轴互相平行，其安装方位如图1所示。三轴磁强计的测量坐标系(OXmYmZm)和卫星本体坐标系的几何关系如图2所示。

图1 三轴磁强计在卫星中的方位Fig.1 Location of three-axis magnetometer in body of satellite

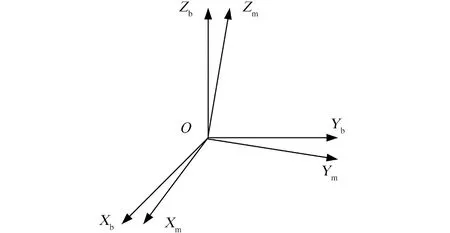
图2 三轴磁强计测量坐标系与卫星本体坐标系Fig.2 Three-axis magnetometer measurement coordinate and body coordinate of satellite

三轴磁强计的输出磁场强度Bb(已经过安装矩阵变换到卫星本体坐标系中)与Bm(基于测量坐标系)之间的关系，可参考泊松模型[12]表示为

Bb=ABm+b

(1)

式中：A为3×3系数矩阵；b为3×1零位电压矩阵。

根据目前已知的三轴磁强计数学模型[12]，无论三轴磁强计的各种误差如何，均可用泊松模型中的矩阵A与b描述。例如，对于三轴磁强计本身因制造和装配工艺而产生的零位误差、标度系数(灵敏度)误差与非正交误差，零位误差即矩阵b，标度系数误差主要表现在矩阵A的对角元，而矩阵A的非对角元则反映了非正交误差。对于载体磁场强度所造成的干扰，矩阵A描述了与地磁场强度呈线性关系的干扰，即软磁干扰；矩阵b则表征了相对于卫星本体坐标系固定不变的干扰，即硬磁干扰。

对于输出为电压模拟量的三轴磁强计，参考泊松模型建立其测量模型。输出电压Um、标定系数矩阵F和输入磁场强度Bb之间的关系为

Um=FBb+U0，m

(2)

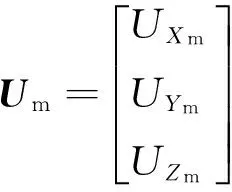
整理可得

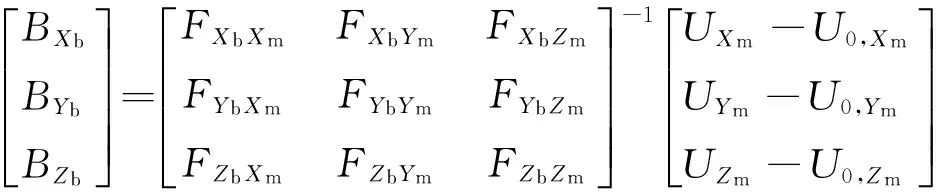
(3)

令

(4)

则三轴磁强计的测量模型可表示为

(5)

在零位电压U0，m的计算中，为了不引入偶然误差，以线圈磁场强度为0 nT时三轴磁强计的输出电压作为零位电压，不同温度下计算出来的零位电压对温度进行线性拟合，得出最终的零位电压表达式。

在标定系数矩阵F的计算中，不同温度下，线圈磁场强度的梯度变化、三轴磁强计输出电压和已拟合得到的零位电压，可构成线性方程组。对于超定线性方程组，采用伪逆法可求出其最小二乘解。根据不同温度下得出的标定系数对温度进行线性拟合，得出最终的标定系数矩阵。

1.2 磁场强度的计算过程

1)温度的计算

根据不同温度下三轴磁强计的温度电压输出，线性拟合出温度计算公式如下。

T=(Ut-Ui)/k

(6)

式中：T为环境温度，℃；Ut为三轴磁强计的温度测量输出电压，V；Ui为温度测量截距，V；k为温度比例系数，V/℃。

2)零位电压的计算

根据不同温度下磁场强度为0 nT时三轴磁强计的Xm轴、Ym轴、Zm轴磁场电压输出，利用三阶线性拟合得出零位电压的计算公式如下。

(7)

式中：UXm(0)，…，UZm(3)分别为Xm轴、Ym轴、Zm轴磁场电压与温度三阶线性拟合得出的零阶、一阶、二阶和三阶系数。

3)标定系数矩阵的计算

不同温度下，求解超定线性方程组得出不同的标定系数矩阵。利用三阶拟合得出标定系数矩阵和温度的关系式如下。

(8)

式中：F11(0)，…，F33(3)分别为标定系数矩阵F的9个矩阵元与温度进行三阶线性拟合得出的零阶、一阶、二阶和三阶系数。

4)磁场强度的计算

根据三轴磁强计的四路遥测电压，由式(6)～(8)计算三轴磁强计的零位电压和标定系数矩阵，根据式(5)可得出三轴磁强计的测量磁场强度。

2 测试及结果分析

2.1 温度建模系数及零位电压系数

标定测试中，温度范围为-30～+60 ℃，温度测量步长为10 ℃，磁场强度为0 nT的情况下线圈温度和三轴磁强计的四路遥测电压关系见表1。根据测试可得出温度建模系数(见表2)和零位电压系数(见表3)。

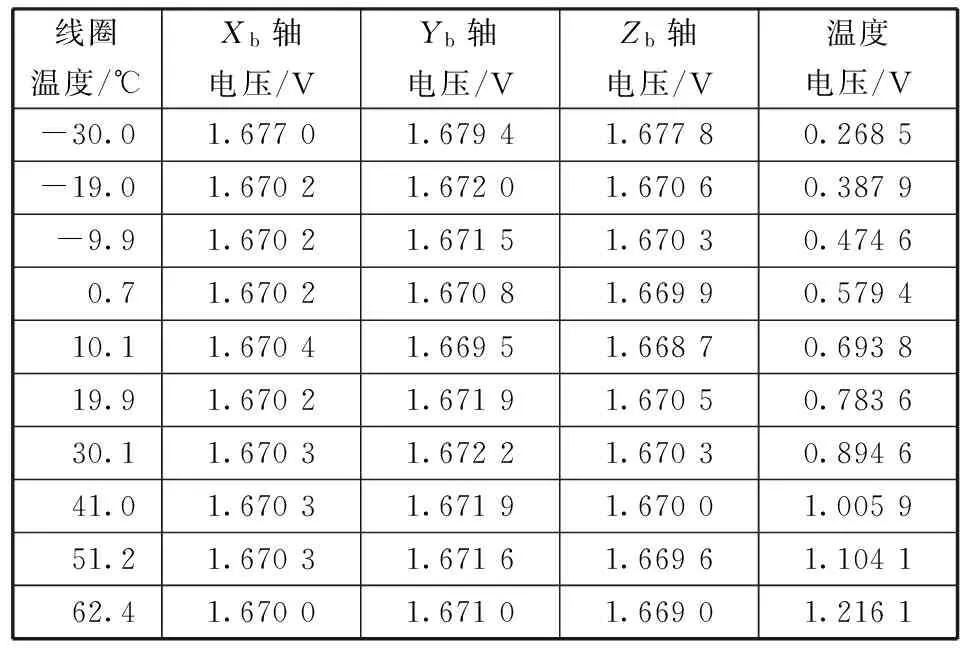
表1 温度建模系数及零位电压系数计算的测试数据

表2 温度建模系数

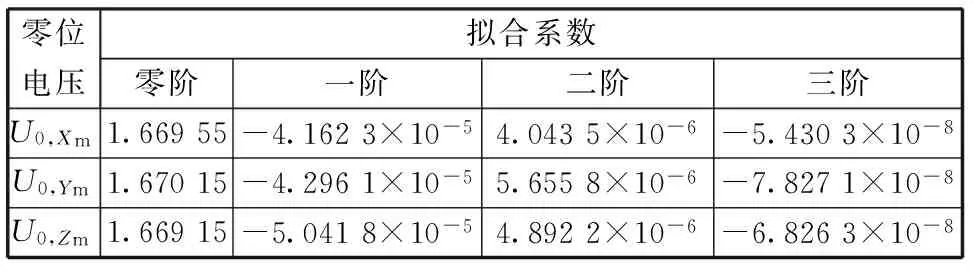
表3 零位电压系数

2.2 标定系数矩阵

标定测试中，磁场强度范围为-80 000～+80 000 nT，磁场强度设定步长为20 000 nT。标定中采用单轴标定，即给三轴磁强计X轴加变化磁场时，Y轴和Z轴的磁场强度为0 nT。根据上文中三轴磁强计磁场强度测量的建模方法，利用伪逆法求解超定线性方程组，并对温度进行三阶拟合，可得标定系数矩阵拟合系数，见表4。

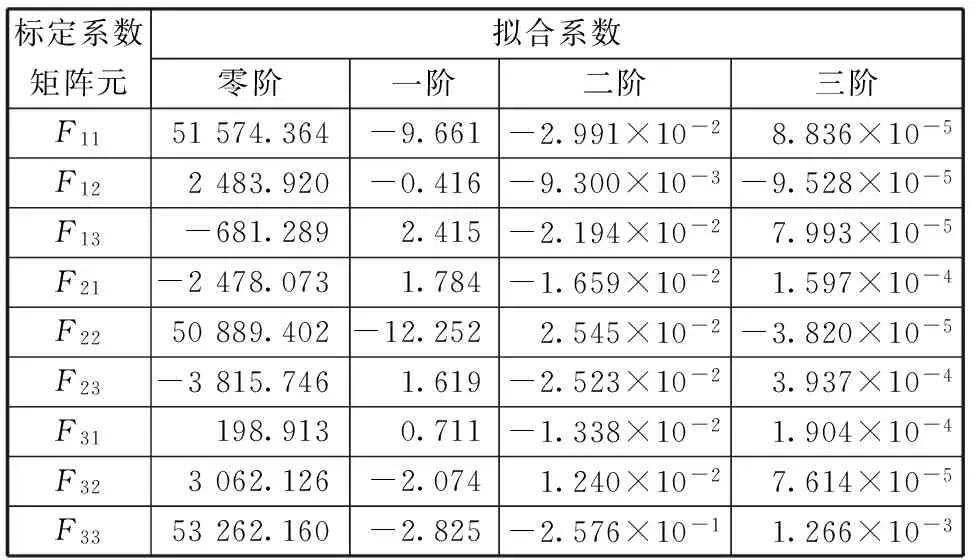
表4 标定系数矩阵拟合系数

2.3 测试结果分析

线圈磁场强度分别为±80 000 nT、±40 000 nT和0 nT时，对标定前后三轴磁强计的三轴测量误差(测量值和标称值之差)和模值误差(三轴测量值平方和的开方值与标称值之差)进行对比，见图3～7。可以看出：标定前X轴、Y轴和Z轴的测量误差最大可达700 nT，1400 nT， 1150 nT，模值误差最大可达1500 nT，不同温度下的测量误差波动很大。经过标定后的三轴磁强计，测量误差可控制在300 nT以内，测量精度明显高于标定前，姿态确定精度在0.8°以内，可满足一般微小卫星的姿态确定要求[13]，充分体现了本文方法的实用性。由于本文采用伪逆法对三轴磁强计的测量误差进行修正，因此标定后的测量误差为统计意义上的最优解，会存在不同磁场强度测量点误差修正差异，即存在波动现象；此外，三轴磁强计正负向敏感轴的不一致性，也会导致正负向磁场强度误差标定的波动性不一致。

图3 标定前后的误差(+80 000 nT磁场强度)Fig.3 Errors under +80000nT magnetic field intensity before and after calibration

图4 标定前后的误差(+40 000 nT磁场强度)Fig.4 Errors under +40000nT magnetic field intensity before and after calibration

图5 标定前后的误差(0 nT磁场强度)Fig.5 Errors under 0nT magnetic field intensity before and after calibration

图6 标定前后的误差(-40 000 nT磁场强度)Fig.6 Errors under -40000nT magnetic field intensity before and after calibration

图7 标定前后的误差(-80 000 nT磁场强度)Fig.7 Errors under -80000nT magnetic field intensity before and after calibration

3 结束语

本文对三轴磁强计的测量误差进行分析，对三轴磁强计的校正原理进行数学建模并推导，利用伪逆法计算三轴磁强计的标定系数。利用标定系数和零位电压对温度进行线性拟合，对三轴磁强计的测量进行温度补偿，最后基于该模型在温度可变的磁环境模拟器中对三轴磁强计进行测试。测试结果表明，本文方法能有效地将磁场强度单轴测量误差控制在300 nT以内，明显高于标定前的精度，可满足一般微小卫星的姿态确定要求。由于产品的差异性，标定后的测量误差不是简单的重复性关系，但是采用本文的标定方法均可达到很好的标定效果。

References)

[1] 章仁为.卫星轨道姿态动力学与控制[M].北京：北京航空航天大学出版社，1998：208

Zhang Renwei. Satellite orbit and attitude dynamics and control [M]. Beijing: Beihang University Press, 1998: 208 (in Chinese)

[2] 盛蔚,蒋勇.三轴磁传感器系统在线标定[J].弹箭与制导学报,2015,35(3):179-182

Sheng Wei, Jiang Yong. Anon-line calibration method of three-axis magnetic sensor system [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2015, 35(3): 179-182 (in Chinese)

[3] 郝东,绳涛,陈小前.三轴磁强计测量误差修正方法[J].航天器环境工程,2011，28(5):463-466

Hao Dong, Sheng Tao, Chen Xiaoqian. The error correction of three-axis magnetometer measurement [J]. Spacecraft Environment Engineering, 2011，28(5):463-466 (in Chinese)

[4] 吴志添,武元新,胡小平，等.基于总体最小二乘的捷联三轴磁力仪标定与地磁场测量误差补偿[J].兵工学报,2012,33(10):1202-1209

Wu Zhitian, Wu Yuanxin, Hu Xiaoping,et al.Calibration of strapdown three-axis magnetometer and measurement error compensation of geomagnetic field based on total least squares [J]. Acta Armamentarii, 2012, 33(10): 1202-1209 (in Chinese)

[5] 费洁,杨英东,王伟栋，等.基于遗传算法的航姿参考系统最小二乘磁标定方法研究[J].微型电脑应用,2013,29(11):17-19

Fei Jie, Yang Yingdong, Wang Weidong， et al. A study of magnetic calibration in navigation system based on LS and genetic algorithm [J]. Microcomputer Applications, 2013, 29(11): 17-19 (in Chinese)

[6] J C Springmann. Attitude-independent magnetometer calibration with time-varying bias [J]. Journal of Gui￣dance, Control, and Dynamics, 2012， 35(4)： 1080-1088

[7] Alonso R, Shuster M D. Complete linear attitude-independent magnetometer calibration [J]. Journal of the Astronautical Sciences, 2002， 50(4)：477-490

[8] Eugnhyun Kim. Attitude-independent magnetometer calibration considering magnetic torquer coupling effect [J]. Journal of Spacecraft and Rockets, 2011, 48(4)： 691-694

[9] Bertrand Grandvallet, Ali Zemouche.Real-time attitude-independent three-axis magnetometer calibration for spining projecties: a sliding window approach [J]. IEEE Transactions on Control Systems Technology, 2014， 22(1)：255-264

[10] Maryam Kiani, Seid H Pourtakdoust. Consistent calibration of magnetometers for nonlinear attitude determination [J]. Measurement, 2015, 73(5)：180-190

[11] Takaya Inamori, Nobutada Sako. Strategy of magnetometer calibration for nano-satellite missions and in-orbit performance [C]//Proceedings of AIAA Gui￣dance, Navigation, and Control Conference, 2010. Washington D.C.： AIAA, 2010： 25-32

[12] Barber G W, Arrott A S. History and magnetics of compass adjusting [J]. IEEE Transactions on Magne￣tics, 1988, 24(6): 2883-2885

[13] 张锐,朱振才，张静，等.基于磁强计的微小卫星姿态确定[J].宇航学报,2006,27(4):578-581

Zhang Rui, Zhu Zhencai，Zhang Jing， et al. Micro-satellite attitude determination based on magnetometer [J]. Journal of Astronautics, 2006, 27 (4): 578-581 (in Chinese)