木星系及行星际飞越探测的多次借力飞行轨道设计研究
2018-02-28田百义张磊周文艳朱安文
田百义 张磊 周文艳 朱安文
(北京空间飞行器总体设计部,北京 100094)
木星是太阳系从内向外的第五颗行星,是太阳系中体积最大、自转最快的行星。其公转轨道的半长轴约7.785 4×108km,绕太阳公转的周期约4 332.59天,约合11.86年。木星赤道地区的自转周期为9小时55分30秒,两极地区的自转周期稍慢一些,木星不同纬度自转周期的不同,说明木星表面是由流体组成的。此外,木星是迄今为止具有最多卫星的行星,已发现66颗天然卫星,因此常被称为木星系统。其中50颗直径小于10 km的卫星,是在1975年以后发现的。1610年,伽利略最早用望远镜发现木星最亮的4颗卫星,被后人称为伽利略卫星,这4颗卫星环绕在离木星4×105~1.9×106km的轨道带,由内而外依次为木卫一、木卫二、木卫三和木卫四,除四颗伽利略卫星外,其他卫星大多是半径几千米到20 km的岩石天体。
开展木星探测,有助于了解太阳系形成、演化的过程和行星系统的起源,同时,木星的4颗伽利略卫星也极具科学价值。截至2017年11月,人类已发射了包括伽利略任务和朱诺任务在内的十余颗探测器已造访木星系统,已规划的木星系探测任务包括欧洲的“木星冰卫探测”(JUICE)任务(预计2020年)和美国的“快帆”任务(预计2022年)等,也将开展木星环绕探测,以及木星卫星的环绕或多次飞越探测。
本文根据我国木星系及行星际穿越探测任务规划,瞄准工程方案可行,对多次借力的地木转移轨道及木星借力后的星际飞行轨道进行优化设计,为我国木星系及行星际穿越探测任务的工程实施提供参考。
1 行星借力模型概述及任务约束分析
1.1 行星借力模型概述
当探测器在主天体引力场中近距离飞越第二个天体(第二天体在主天体引力范围内运行)时,第二个天体的引力将改变探测器在主天体引力场中的运行轨道。以星际飞行为例,主天体为太阳,第二天体为行星(如水星、金星、地球、火星、木星等八大行星),行星借力可用来改变探测器相对太阳的轨道能量或轨道倾角(或两者同时改变)。
以地球借力飞行为例,图1给出了两类地球借力飞行轨道:能量增加型和能量减小型。地球借力飞行的轨道相对地球而言,是一条以地心为焦点的双曲线轨道,探测器在地球影响球边界处相对探测器的速度为双曲线剩余速度V∞,在探测器自由飞行状态下,地球借力前后的V∞大小相等,即‖V∞in‖=‖V∞out‖,因此探测器相对地球的轨道能量没有变化。地球借力的效果是造成了探测器V∞旋转了一个角度θ,称为“借力转角”。探测器借力的时间相对地球公转周期短的多,可认为探测器飞入/飞出地球影响球时的位置矢量不变。借力转角造成探测器飞出地球引力范围后,相对太阳的速度大小和方向发生了变化(见图1),因此,探测器绕日飞行轨道能量也就发生了改变。
(1)“能量增加型”借力:探测器由地球后方飞越,地球借力之后V∞顺时针旋转,将V∞与VEarth矢量相加,显然有VS/Cout>VS/Cin,见图1(a),因此地球借力增大了探测器相对太阳的轨道能量;
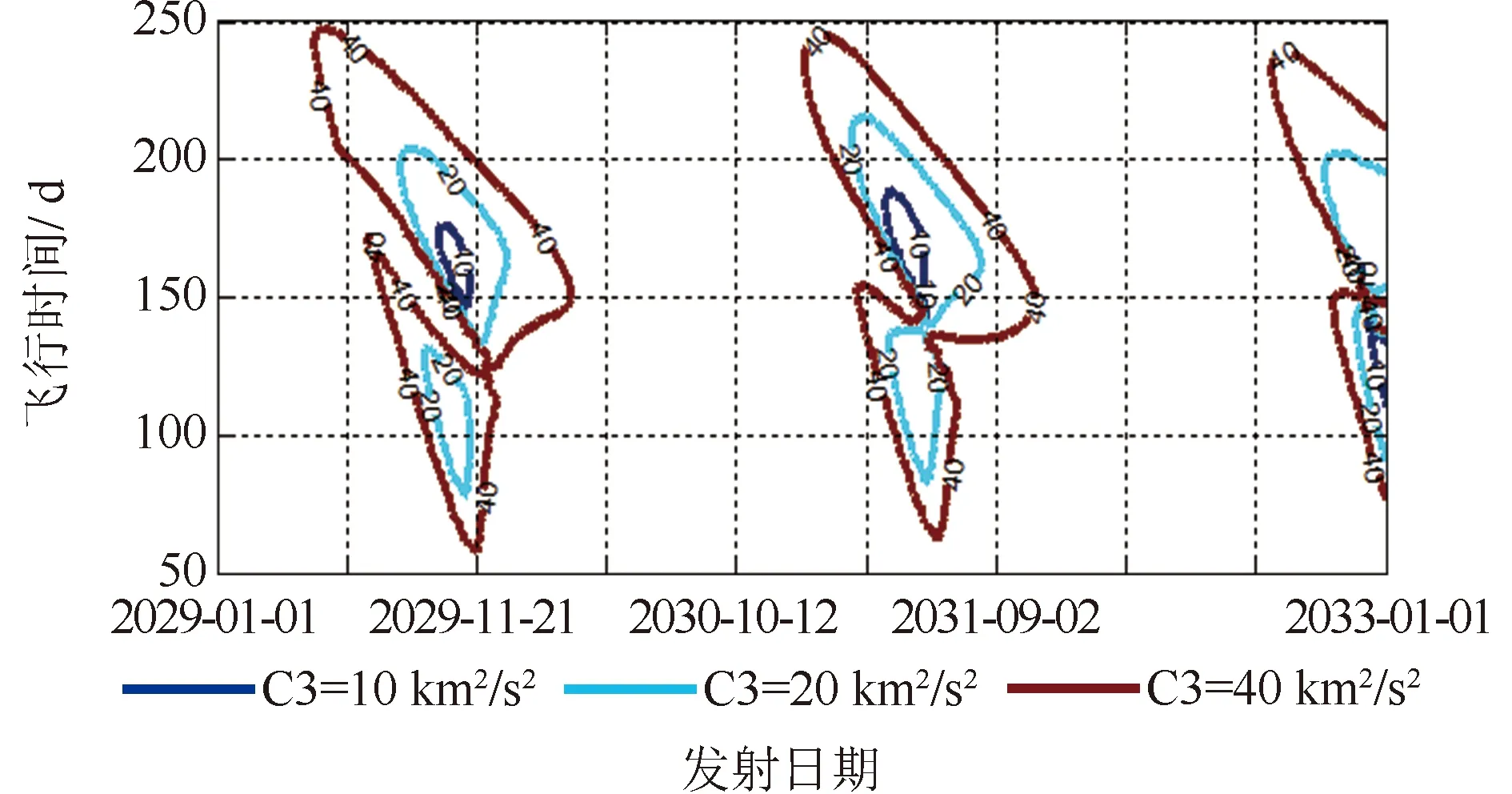
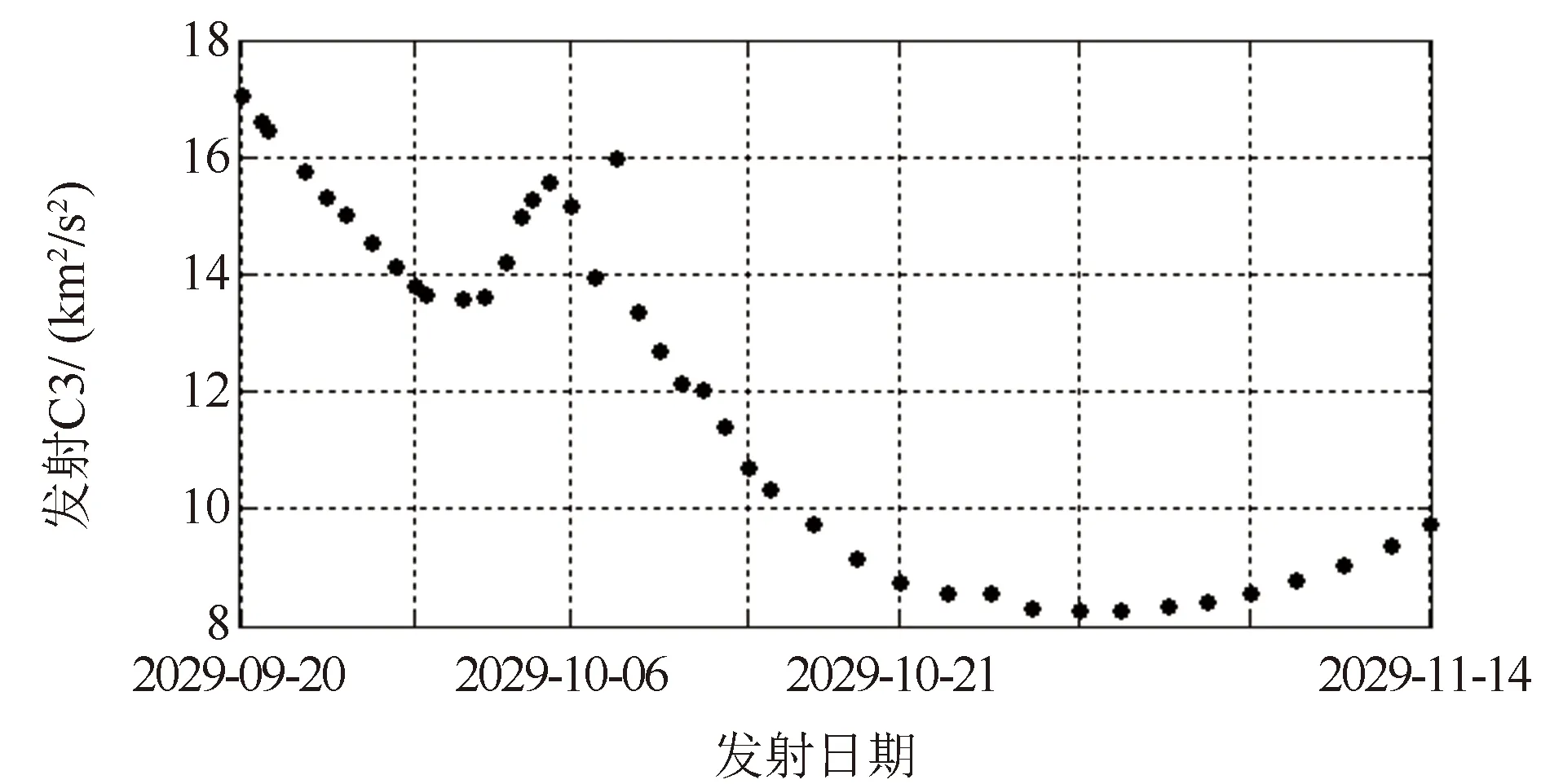
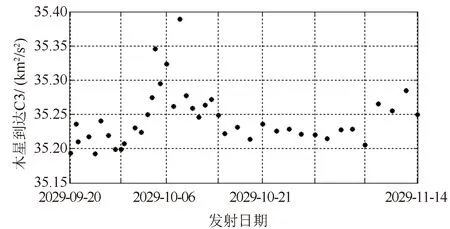
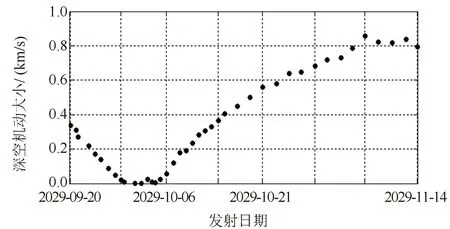
(2)“能量减小型”借力:探测器由地球前方飞越,地球借力之后V∞逆时针旋转,将V∞与VEarth矢量相加,显然有VS/Cout 借力转角θ与探测器飞越地球的双曲线剩余速度V∞和近地点半径rp具有如下关系: (1) 式中:μe为借力天体-地球的引力常数。 当借力天体为其他行星时,原理相同,此处不再赘述。 根据我国目前航天技术发展现状和未来的航天任务规划,对木星系及行星际穿越探测任务提出如下约束: (1)瞄准工程可行,飞行方案应满足运载系统发射双曲剩余速度的平方(C3)、射向、滑行时间和落区安全等约束,以及满足发射场系统提出的连续多天发射条件; (2)地木转移阶段,考虑地球(E)、地球-金星(EV)、金星-地球-地球(VEE)和金星-金星-地球(VVE)四种借力序列,择优选择; (3)发射日期选择在2030年前后,木星借力之后的行星飞越目标选择天王星或海王星,且约束探测器在2049年之前飞越目标; (4)探测器由木星系环绕器和行星际飞越器组成,总质量5000 kg,其中木星系环绕器质量4000 kg,行星际飞越器1000 kg。 为实现整体任务的最优化设计,将地木转移段轨道与木星-天王星或海王星轨道进行联合优化。为满足木星系的探测任务需求,增加木星借力时的C3约束为:不大于50 km2/s2,以减小木星捕获时的速度增量需求。 探测器在到达木星之前,释放行星际飞越器,经过木星借力之后飞往天王星,因此,可根据木星-天王星的C3能量等高线图得到探测器适宜到达木星的时间情况。 图2给出了木星-天王星出发C3能量等高线图,图中每个点均代表了一条经木星借力后飞往天王星的轨道,同一颜色的线代表探测器飞越木星时的C3相同。由图2可知:满足2049年之前到达天王星且飞越木星C3小于50 km2/s2的木星借力日期在2036年10月之前。而地木转移的轨道飞行时间一般为3~7年,因此,探测器从地球发射的日期应在2033年10月之前,满足探测任务的时间规划。 图2 木星-天王星发射C3能量等高线图Fig.2 Jupiter- Uranus launch C3 energy 综上可知,天王星飞越探测满足任务时间规划,是潜在可行的行星飞越探测目标。 与天王星为飞越目标的分析过程类似,图3给出了木星-海王星的出发C3能量等高线图。 图3 木星-海王星出发C3能量等高线图Fig.3 Jupiter-Neptune launch C3 energy 由图3可知:满足2049年之前到达海王星且飞越木星C3小于50 km2/s2的木星借力日期在2032年10月之前。而地木转移的轨道飞行时间一般为3~7年,因此,探测器从地球发射的日期应在2029年10月之前,不满足探测任务的时间规划。 综上可知,不适宜选择海王星作为行星飞越探测目标。 根据上述分析,确定选择天王星作为后续行星飞越目标。为实现探测任务的整体最优性,采用差分进化算法,将地木转移段轨道与木星-天王星轨道进行联合优化。重点分析地球-地球-木星-天王星(EEJU)、地球-金星-地球-木星-天王星(EVEJU)、地球-金星-地球-地球-木星-天王星(EVEEJU)和地球-金星-金星-地球-木星-天王星(EVVEJU)4种行星飞行序列。为减小借力时行星大气和磁场等环境因素对探测器的影响,结合探测器深空测定轨精度与热防护能力,一般要求类地行星借力飞越安全高度不低于200 km,因此优化设计时增加行星借力高度约束如下:①金星借力高度≥300 km;②地球借力高度≥300 km;③火星借力高度≥300 km;④木星借力高度≥4RJ(RJ=71 492.00 km为木星半径)。 表1给出了仅考虑运载发射C3约束情况下的四种序列星际飞行轨道优化设计结果。由于EEJU和EVVEJU两种序列无满足发射C3约束的最优解,因此,优化时适当地放宽了此两种序列的发射C3约束。根据表1,综合考虑探测器发射日期、发射C3(或最大发射质量)、木星到达C3、深空机动大小(燃料消耗)和总的任务时长满足任务情况(按优、良和差三种区分),得到四种序列的对比结果(见表2),可见四种星际飞行序列的最优排序为:EVEEJU,EVEJU,EVVEJU,EEJU。其中EVEEJU和EVEJU两种序列满足工程需求,本文选取这两种序列进行优化对比分析。 表1 四种序列的星际飞行任务轨道优化设计结果 表2 四种序列的任务满足情况评价结果 木星系及行星际穿越探测任务采用首次金星借力的星际飞行序列,因此,地球-金星的窗口即决定了整个探测任务窗口。图4给出了2029—2033年期间的地球-金星发射C3能量等高线图,由图可知:满足运载发射C3约束的探测器最优发射日期集中在2029年10月份和2031年8月份。其中2029年10月份窗口对应的星际飞行序列为EVEEJU,2031年8月份窗口对应的星际飞行序列为EVEJU。 图4 地球-金星发射C3能量等高线图(2029—2033年)Fig.4 Earth-Venus launch C3 energy (2029—2033) 木星系及行星际穿越探测任务的发射窗口与我国运载水平紧密相关,表1的全局最优发射窗口和图4的连续发射日期,不一定满足我国运载的射向和滑行时间等约束,以及工程总体对连续发射日期的需求,因此开展发射窗口优化设计时必须引入具体工程约束。 以图4的窗口为初值进行连续发射窗口的优化设计,图5至图7分别给出了EVEEJU序列的探测器发射C3、木星到达C3和深空机动大小随发射日期的变化情况,可知:探测器最优的发射日期集中在2029年9月24日—2029年10月09日(连续16天),探测器发射所需的发射C3均小于16.0 km2/s2,木星到达C3约35.4 km2/s2,且深空机动需求不大于200 m/s。其中,9月26日-10月6日(连续11天)发射的深空机动小于100 m/s;9月28日—10月5日(连续8天)发射的深空机动小于50 m/s。 图5 探测器发射C3随发射日期的变化情况(EVEEJU)Fig.5 Launch C3 energy for EVEEJU 图6 木星到达C3随发射日期的变化情况(EVEEJU)Fig.6 Jupiter arrive C3 energy for EVEEJU 图7 探测器深空机动大小随发射日期的变化情况(EVEEJU)Fig.7 DSM(Deep Space Maneuver) budget for EVEEJU 通过优化设计,图8至图10分别给出了EVEJU序列的探测器发射C3、木星到达C3和深空机动大小随发射日期的变化情况,可知:探测器最优的发射日期集中在2031年7月27日—2031年8月16日(连续11天),探测器发射所需的发射C3均在19 km2/s2左右,木星到达C3约40.5 km2/s2,深空机动需求为840~1140 m/s。 图8 探测器发射C3随发射日期的变化情况(EVEJU)Fig.8 Launch C3 energy for EVEEJU 图9 木星到达C3随发射日期的变化情况(EVEJU)Fig.9 Jupiter arrive C3 energy for EVEJU 图10 探测器深空机动大小随发射日期的变化情况(EVEJU)Fig.10 DSM budget for EVEJU 根据4.1节和4.2节的分析,两种飞行序列对应的深空机动(星际飞行燃料消耗)、发射C3(运载发射能力)和木星到达C3(木星捕获燃料消耗)均具有差异(假设探测器轨控发动机比冲为315 s): (1)星际飞行燃料消耗。EVEJU飞行序列较EVEEJU飞行序列深空机动增加约700 m/s,对应的燃料消耗量增加1000 kg; (2)运载发射能力。EVEJU飞行序列较EVEEJU飞行序列发射C3大3 km2/s2左右,对应的运载发射质量减小约290 kg; (3)木星捕获燃料消耗。EVEJU飞行序列较EVEEJU飞行序列的木星到达C3大5 km2/s2左右,对应的木星捕获燃料消耗增加约50 kg。 综上,EVEJU飞行序列的探测器干重预算较EVEEJU飞行序列减小近1340 kg,因此,EVEEJU飞行序列具有更优的特性,应为我国木星系及行星际穿越探测任务的首选。 本文以工程可行为目标,针对木星系及行星际穿越探测任务的星际飞行方案进行了深入研究和分析,研究结果表明: (1)天王星适宜作为我国首次木星系及行星际穿越探测任务的星际探测目标,探测器可于2045年前后飞抵天王星; (2)2029—2032年期间,四种星际飞行序列的最优排序为:EVEEJU,EVEJU,EVVEJU,EEJU。EVEEJU飞行序列具有最优的特性,应为我国木星系及行星际穿越探测任务的首选; (3)EVEEJU飞行序列满足任务约束的发射日期集中在2029年10月份前后。 本文研究结果可为我国木星系及行星际穿越探测任务论证与规划提供参考,后续可根据任务总体需求,及我国未来运载火箭和航天器发展情况开展详细的轨道方案优化设计,对星际飞行过程中涉及的能源、空间环境、通信弧段、天体遮挡等具体工程问题开展深入研究与分析,为我国首次木星系及行星际穿越探测任务的工程实施提供技术保障。 References) [1] 中国科学院月球与深空探测总体部. 月球与深空探测[M]. 广州:广东科技出版社, 2014: 434-436 Lunar and Deep Space Exploration Department of Chinese Academy of Sciences. Lunar and deep space exploration[M]. Guangzhou: Guangdong Science and Technology Press, 2014:434-436 (in Chinese) [2] The JUICE Scicence Study Team. JUICE exploring the emergence of habitable worlds around gas giants[R]. Paris: ESA, 2011 [3] Michael Meltzer. Mission to Jupiter:a history of the Galileo project, NASA SP-2007-4231[R]. Washington D.C.:NASA, 2007 [4] T Kowalkowski,J Johannesen,T Lam. Launch period development for the Juno mission to Jupiter[C]// AIAA/AAS Astrodynamics Specialist Conference and Exhibit. Washington D.C.: AIAA, 2008:1-13 [5] L J Miller, J K Miller, W E Kirhofer. Navigation of the Galileo mission[C]// 21st Aerospace Sciences Meeting. Washington D.C.:AIAA, 1983: 1-19 [6] Matteo Ceriotti. Global optimization of multiple gravity assist trajectories[D]. Glasgow: University of Glasgow, 2010 [7] Betts J T. Survey of numerical methods for trajectory optimization[J]. Journal of Guidance, Control, and Dynamics, 1998, 21(2): 193-207 [8] 田百义. 小推力借力转移轨道设计与优化方法研究[D]. 哈尔滨:哈尔滨工业大学, 2012:30-45 Tian Baiyi. Design and optimization of low-thrust gravity-assist trajectories[D]. Harbin: Harbin Institute of Technology, 2012:30-45 (in Chinese) [9] 董捷, 孟林智, 赵洋,等. 国外木星系环绕飞行任务规划研究[J]. 航天器工程,2015, 24(3):85-92 Dong Jie, Meng Linzhi, Zhao Yang, et al. Demonstration of foreign Jovian system orbiting mission plan[J]. Spacecraft Engineering, 2015, 24(3): 85-92 (in Chinese)1.2 任务约束分析
2 行星飞越目标选择
2.1 天王星
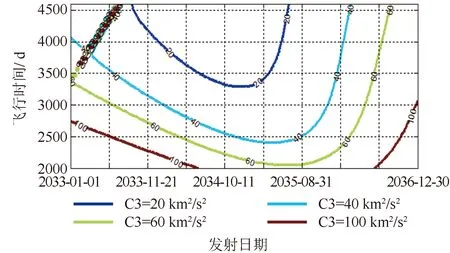
2.2 海王星
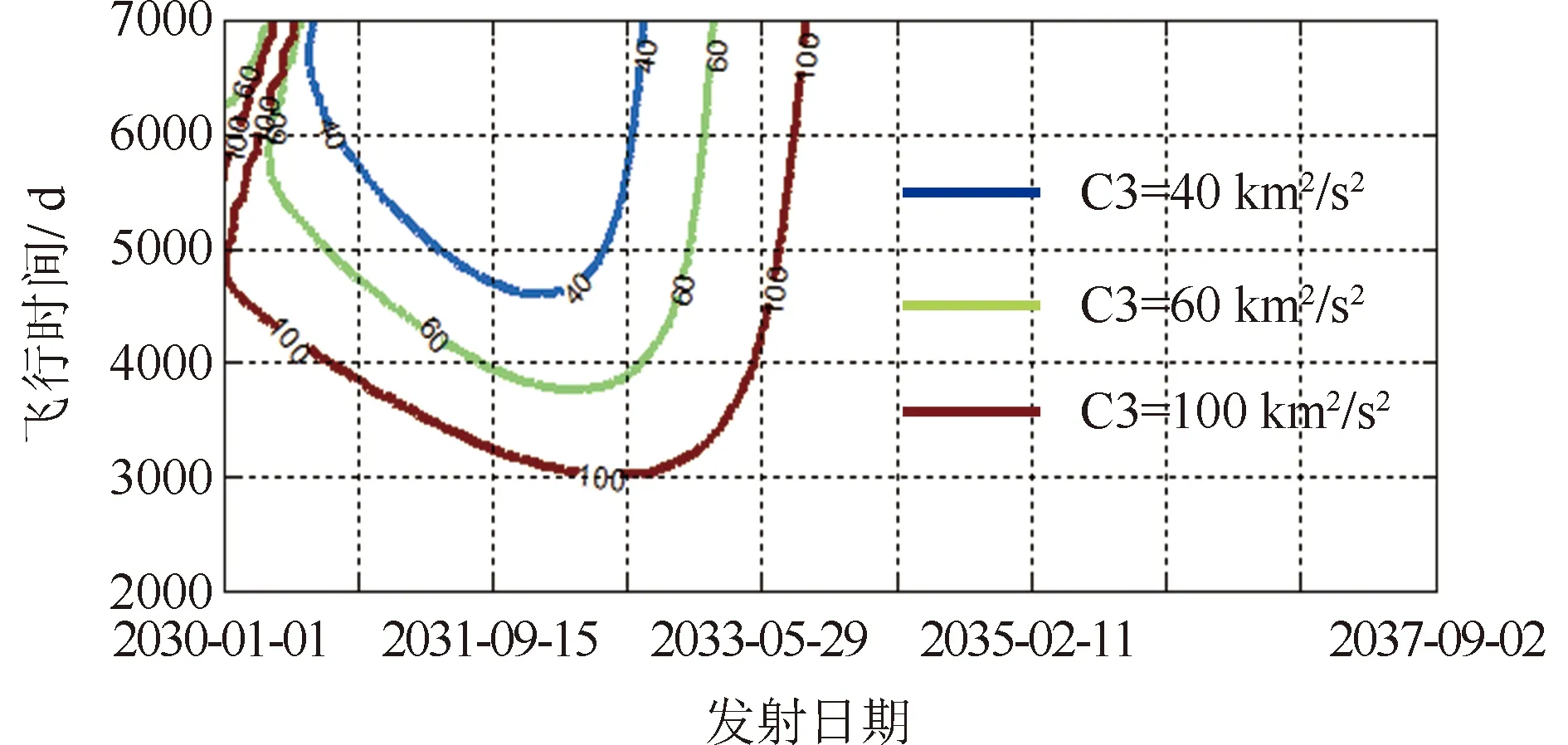
3 星际飞行序列的优选
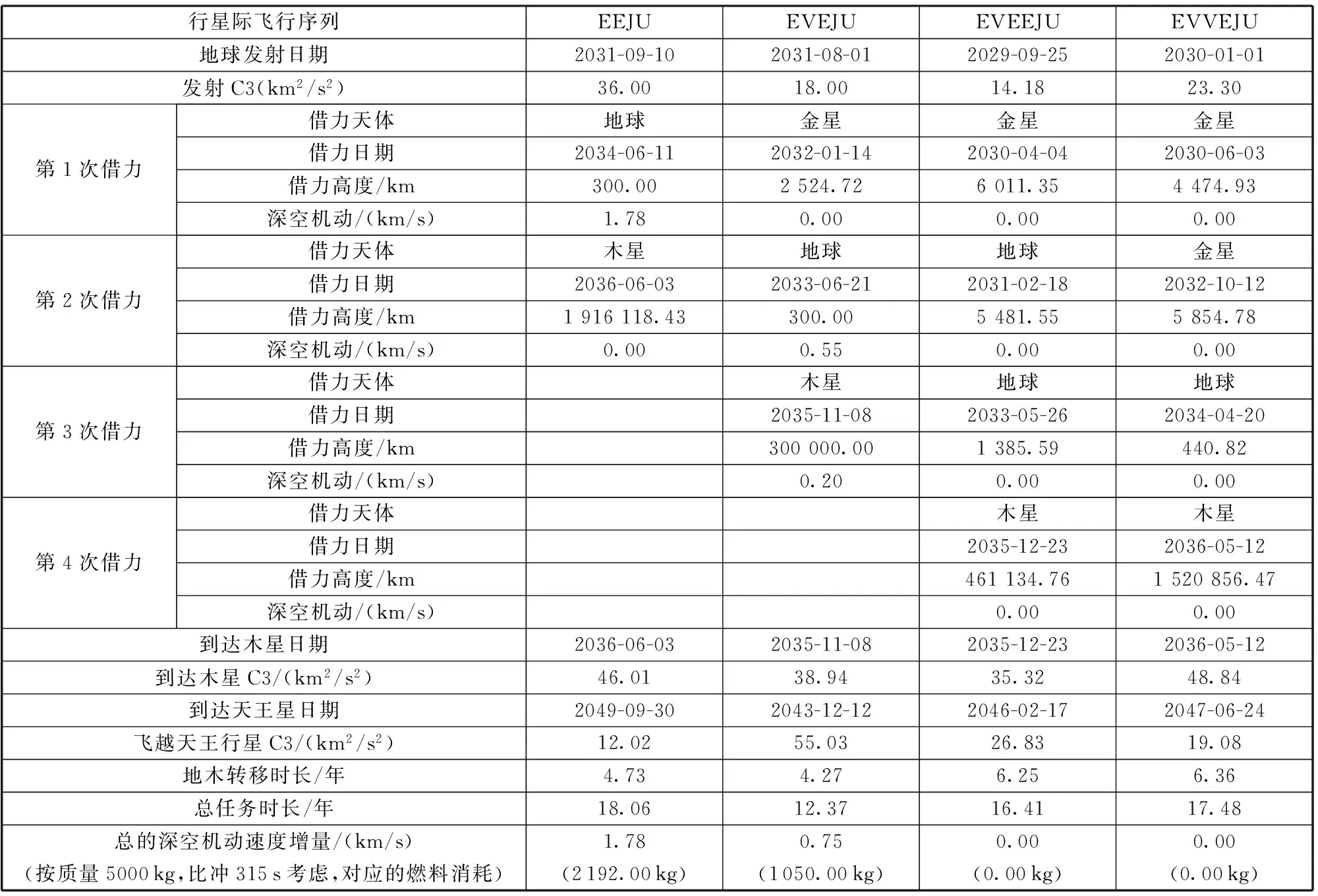
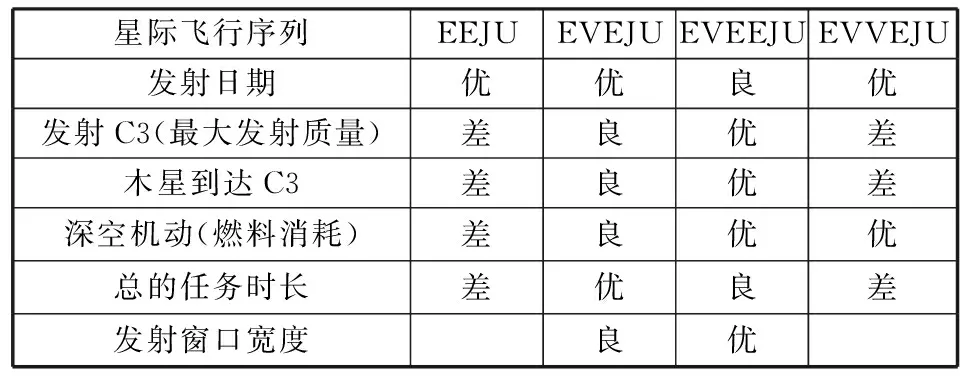
4 连续发射日期优化分析
4.1 EVEEJU飞行序列
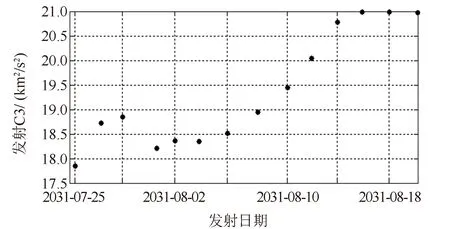
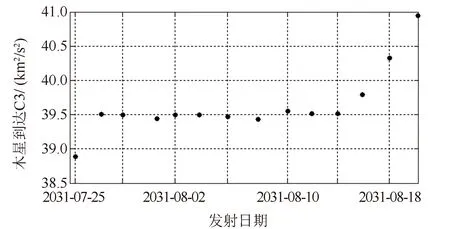
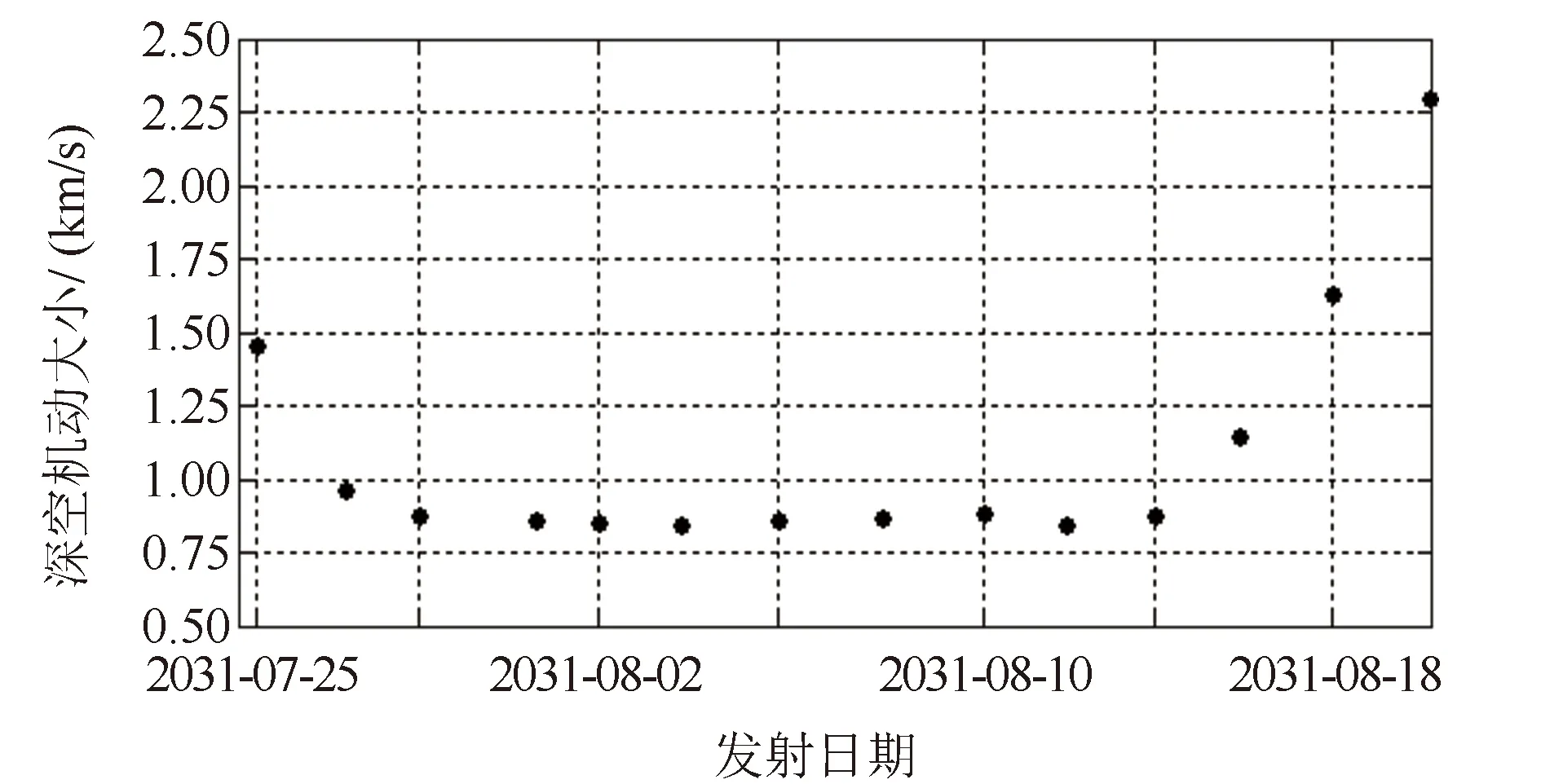
4.2 EVEJU飞行序列
4.3 两种飞行序列的对比分析
5 结束语
