基于响应面法的内燃机曲轴优化
2018-02-28王虎洪锦裴精精
王虎,洪锦,裴精精
(合肥工业大学机械工程学院,安徽 合肥 230009)
曲轴作为内燃机动力转换和传递的核心部件,其结构强度在很大程度上决定了内燃机的可靠性和寿命,因此,对曲轴结构强度的安全考核是内燃机设计过程中的一项重要内容。为使曲轴强度的预测更加准确,曲轴的设计更加合理,国内外研究人员主要从试验测试和仿真计算两方面开展研究工作[1]。对实际运行中的曲轴进行强度测试,难度大、精度难保证,而且以测量分散的点数据为主,无法获得曲轴整体的应力状况,对最危险部位的预测仍以实际经验判断为主。试验测试一般均在成品中进行,很难在设计阶段应用。随着数值方法和计算机技术的发展,对曲轴的计算分析也由简化的简支梁法、连续梁法逐渐发展到整体曲轴的有限元法[2-6],实践证明,基于有限元法对曲轴进行结构分析和优化是曲轴设计分析最有力的工具之一。
基于数值方法的内燃机曲轴优化研究主要分两种:第一种是通过对若干预设尺寸曲轴数值结果的比较获得较优解[2-4];第二种是以数值计算为基础,通过试验设计、拟合近似和优化方法相结合来获得最优化方案[5-6,8]。显然,第二种方案更准确更完善,它将数值模拟、优化方法通过试验设计和近似拟合有效结合在一起,适用面更广,可选择的方法组合更丰富,针对性更强。本研究采用有限元、响应面法和协同优化的组合,对曲轴进行优化设计。研究中充分考虑了内燃机的实际工况,对曲轴进行有限元整体建模,再通过中心组合试验设计采样,结合最小二乘法和显著性分析,构建曲轴结构参数与最大应力及最大变形量的响应面近似模型,运用协同优化算法对其进行优化求解。
1 曲轴有限元模型
1.1 几何模型和网格划分
研究以某直列4缸、水冷、缸径105 mm柴油机曲轴为研究对象,主要结构参数见表1。首先在CATIA中建模,后导入Ansys分析平台。有限元模型采用十节点四面体SOLID187单元,共有360 776个节点,245 209个单元。

表1 曲轴主要结构参数
1.2 边界条件处理
曲轴模型中添加的载荷边界包括轴颈表面压力、曲轴旋转惯性力、重力、主轴颈支反力等。
依据有限宽滑动轴承润滑油膜压力分布特点,沿曲轴连杆轴颈及主轴颈轴线方向载荷分布采用二次抛物线模型;沿轴颈圆周方向以接触点为中心120°范围采用余弦分布模型[2,4](见图1)。
曲轴连杆轴颈轴向载荷分布:
(1)
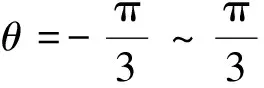
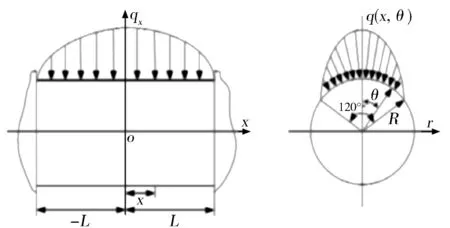
图1 轴颈轴向及周向载荷分布示意
实际工况下,确定曲轴主轴颈支反力时,首先采用简支梁法求得各轴颈处支反力,然后按分布压力施加于主轴颈处,加载方式亦符合二次抛物线规律。
重力以体力的形式给出,旋转惯性力以实际工况下内燃机转速为基准进行计算加载。
曲轴输出端扭矩的施加可采用两种方式:一种将扭矩等效转化为沿径向线性变化的切向力施加在输出轴端面;另一种在曲轴输出端外侧建立MPC184新节点,然后将该节点与输出轴端面周向节点建立刚性连接,施加扭矩于该节点,通过刚性连接将扭矩传递给曲轴。本研究中采用第二种方法。
整体坐标下,限制主轴颈左端圆周面上中心附近节点x,y方向的位移,同时限制右端面中心附近节点x,y,z方向的位移。
1.3 计算结果
一般情况下,4缸内燃机在第2, 3缸最高燃烧压力作用时曲轴受力情况最严峻,因此,本研究选取第2缸最高燃烧压力时刻为计算时间点,计算结果见图2。

图2 曲轴在第2缸最高燃烧压力时刻的综合应力
由图2看出:在第2缸最高燃烧压力点时,最大应力发生在第2连杆轴颈与曲柄过渡圆角处,应力值为141.849 MPa,最大变形量为0.406 978 mm。
2 曲轴优化设计
考虑到曲轴原始设计尺寸的相对合理性,同时为避免抽样点过多,本研究采用成熟的中心组合试验设计获取设计样本点[7]。
2.1 中心组合试验设计
中心组合试验设计方法中,试验次数M表示为[8]
M=mc+mr+m0。
(2)
式中:mc=2n,n为设计变量个数;mr=2n;m0为中心点数。
本次内燃机曲轴的优化设计尽量避免修改关联复杂的整机尺寸,同时考虑曲轴最大应力的重要影响因素,初步将连杆轴颈直径D1、连杆轴颈过渡圆角半径R1、主轴颈直径D2、主轴颈过渡圆角半径R24个因素作为优化设计参数,每个参数在初始值附近选取5个水平,共30个试验抽样点,其中立方体点16个、轴点8个、中心点6个。设计参数的默认值见表1,表2列出曲轴进行中心组合试验的部分有限元计算结果。
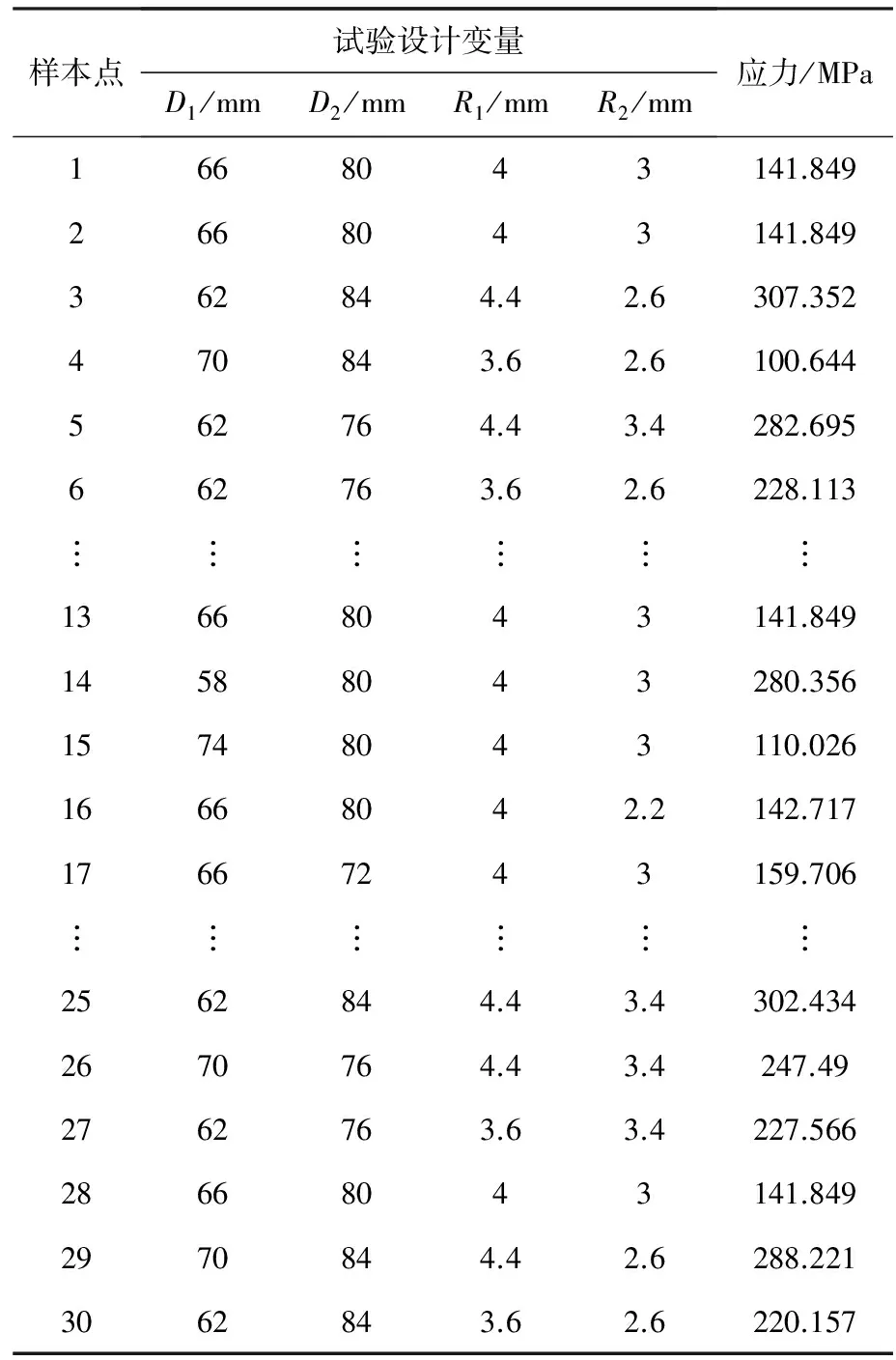
表2 中心组合试验设计的试验结果(部分)
2.2 曲轴响应面模型
响应面法是一种有效构建近似模型的方法[8],综合考虑近似拟合精度和后期优化效率,本次采用二次响应面模型,表达如下:
(3)
式中:n为设计变量数。通过有限元仿真获得曲轴强度M个样本点对应的响应量y=(y(1),y(2),…y(M))T,然后运用最小二乘法估算出响应面系数向量α,表达如下:
α=(φTφ)(-1)(φTy)。
(4)
式中:φ为响应面样本矢量,

(5)
式中:N为响应面模型基函数的个数。从设计样本点及其对应的有限元计算结果确定矩阵φ和响应矢量y,然后代入式(4),求得系数向量α,进而获得响应面表达式。
将试验设计样本点及其对应的有限元结果响应数据代入二次响应面方程,对方程组运用最小二乘法,求得系数(见表3)。
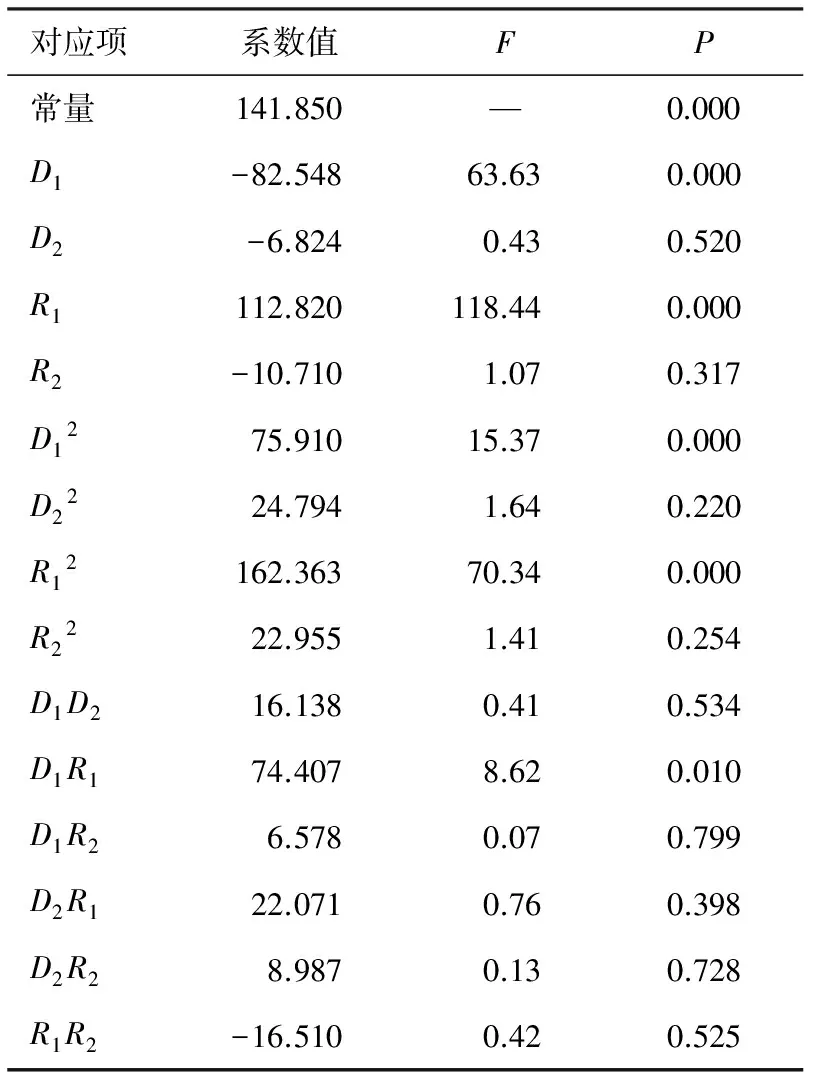
表3 响应面模型系数值及显著性分析
2.3 显著性分析
为保证优化模型的准确性,一般会在开始阶段根据经验选取尽可能多的参数作为初始优化设计变量,此时无法定量评估初始设计变量对考察结果影响的显著性。非显著影响设计变量的加入势必导致优化数学模型过大,严重影响后期的优化效率。影响因素的显著性分析采用方差分析的方法,通过对近似模型的准确性和因素的影响水平进行评价,筛选出显著性影响因素,并对模型进行适当的简化修正,提高优化效率。显著性分析可通过F值确定因素水平改变对试验结果的影响超过试验误差所产生的影响,F值的定义如下:
(6)

从表3可以看出:连杆轴颈直径D1、连杆轴颈过渡圆角半径R1对于目标结果的影响非常显著,而主轴颈直径D2、主轴颈过渡圆角半径R2及其相关二次项对于目标结果的影响不显著,可以忽略,这与有限元仿真计算是吻合的。由于曲轴本身结构和支撑的特点,最大应力一般发生在连杆轴颈过渡圆角处,显然D1,R1对其影响非常显著。一般来说,与曲轴轴颈相比,主轴颈处所受弯矩较小,支撑刚性较好,主轴颈圆角处应力极值一般不会是曲轴应力最大值,所以其结构尺寸对曲轴整体最大应力的影响不显著。
依据表3显著性分析结果,首先对设计参数进行必要优选,筛除二次响应面模型中的不显著因素主轴颈直径D2、主轴颈过渡圆角半径R2,保留连杆轴颈直径D1、连杆轴颈过渡圆角半径R1两个显著因素作为设计变量修正近似模型,结果见表4。
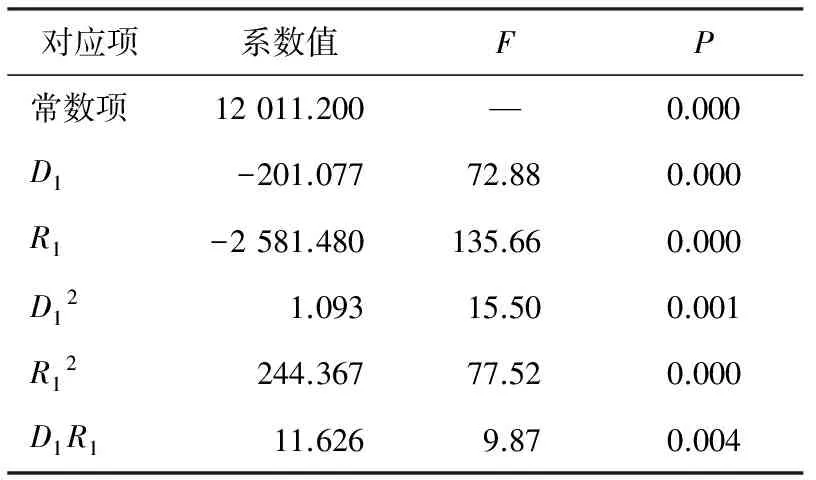
表4 修正响应面模型各系数值及显著性分析
由表4可以看出,修正后的响应面近似模型各因素影响显著,设计变量选取合理,修正后最大应力和最大变形二次响应面近似模型如下:

(7)
Δlmax=10.171 5-0.155 993·D1-
1.840 30·R1+0.030 072 2·D1R1。
(8)
2.4 修正响应面模型的拟合精度
响应面模型拟合精度越高,说明该模型与试验样本点考察结果一致性越好,模型越准确可靠。拟合精度一般通过方差分析中的决定系数R2和调整决定系数Radj2来检验,R2和Radj2定义如下:
(9)
(10)
响应面模型的方差分析中,R2和Radj2越接近1,则响应面模型的拟合精度就越高。
这里对曲轴最大应力修正响应面模型进行拟合精度分析,将通过该响应面模型得到的近似响应值与通过有限元计算的真实值代入上两式,求得此模型的R2和Radj2(见表5)。

表5 修正响应面模型的决定系数和调整决定系数
由表5可知,修正响应面近似模型的决定系数R2和调整决定系数Radj2均大于0.9,说明此模型能很好地拟合有限元计算的结果,可用于后续的优化设计。
2.5 基于协同理论的优化
为提高曲轴强度,将曲轴最大应力最小化确定为优化目标,上述二次响应面近似模型为数学基础,以最大变形量、质量不大于默认工况下的初始值为约束条件,同时对曲轴结构尺寸进行约束:
min[σ(D1,R1)],
s.tl(D1,R1)≤lmax,
m(D1,R1)≤mmax,
Dmin≤D1≤Dmax,
Rmin≤R1≤Rmax。
以ISIGHT为计算平台,运用协同优化理论进行优化,优化计算中使用动态松弛因子,系统级选取模拟退火法,子学科级采用霍克-吉维斯直接搜索法(简称HJ)[10-11]。最终经过1 852次寻优迭代,求得最优解为D1=66.404 mm,R1=3.701 7 mm,最大应力为128.08 MPa,降低9.7%。寻优历程见图3,优化前后结果对比见表6。

图3 HJ方法寻优求解过程

模型设计变量D1/mmR1/mm最大应力σmax/MPa最大变形量Δlmax/mm优化前66.04.0141.850.40698优化后66.43.7128.080.39268
为检验该响应面模型优化结果的准确性,此处以优化后的结构尺寸建立有限元模型并求解,对比响应面模型得到的响应量与相应有限元模型的计算结果(见表7)。由表7可以看出,用该响应面模型得到的最大应力、最大变形数值误差仅为1.226%和1.569%,这表明本次优化所采用的二次响应面模型和协同优化算法具有很高的准确性。

表7 优化结果与有限元结果对比
3 结束语
以中心组合试验方法设计样本点,整体曲轴强度有限元分析获得响应值,构造内燃机曲轴强度的二次响应面近似模型,并通过显著性分析对该模型进行修正,检验了修正模型的拟合精度。
以曲轴最大应力最小为优化目标,曲轴最大变形、质量、结构尺寸为约束条件,运用模拟退火与直接搜索相结合的协同优化算法对曲轴强度二次响应面近似模型进行优化计算。通过优化结果的对比分析可以看出,曲轴强度得到明显提高,优化结果准确可靠,从而验证了本次响应面法和协同优化算法相结合的曲轴优化设计方法的有效性。
[1] 孙军,桂长林,李震.内燃机曲轴强度研究的现状、讨论与展望[J].内燃机学报,2002,20(2):179-184.
[2] 田忠静,王金辉,李海梅.曲轴的参数化有限元分析[J].长春工业大学学报(自然科学版),2011,32(3):283-288.
[3] 文怀军,薛雪华.基于有限元分析的增压发动机曲轴设计优化[J].小型内燃机与车辆技术,2017,46(1):46-49.
[4] 尹建民,王德海,袁银南,等.X6135柴油机曲轴强度的三维有限元研究[J].内燃机工程,1997,18(2):71-77.
[5] 王枫,陈征,李花,等.采用多体动力学的压缩机曲轴结构优化[J].西安交通大学学报,2017,51(3):7-13.
[6] 杨道斋,姜勇,张洪信,等.三缸内燃泵曲轴负荷多学科仿真研究[J].机械设计,2011,28(12):68-73.
[7] 刘文卿.实验设计[M].北京:清华大学出版社,2005.
[8] 程军圣,余淏.基于响应面法的听小骨消声器的优化设计[J].湖南大学学报,2017,44(2):60-65.
[9] PAPILA M.Accuracy of response surface approximations for weight equations based on structural optimization[D].Gainesville:University of Florida,2001.
[10] 王波.协同优化技术在多学科复杂系统设计中的应用[D].西安:西安理工大学,2010.
[11] 裴精精.基于有限元分析的曲轴多学科设计优化[D].合肥:合肥工业大学,2014.
