基于BP神经网络方法的测风塔缺测数据插补分析

文 | 朱晓玲，董金凤，王朝辉

风能资源的评估是整个风电场建设、运行的重要环节，是风电场取得良好经济效益的关键。风能资源评估中最关键的就是测风数据的有效完整性，但在测风时常常因为各种原因出现或多或少的缺失，需要对缺测数据进行合理插补分析，而由于各种因素的影响，往往会给插补结果带来一定偏差。

相关性方法和风切变指数法是目前对风电场测风数据进行插补的主要方法。相关性方法受相关系数影响比较大，尤其是低风速风电场，小风速样本量比较大，会影响相关性方程，继而影响数据插补的精度。而风切变指数法存在着不同风向且不同高度的风切变指数不一样的问题，不同的风切变指数会影响到计算结果的精确度，因此，需要寻找另外一种处理测风数据的有效方法。在现有的人工神经网络模型中，效果最好、应用最广泛的是BP神经网络。BP神经网络不但有非线性无参数的特性，还很适合处理时间序列分布和含噪音的数据，尤其对那些以模糊、不完整、不严密的知识或数据为特征的问题的处理。当前，BP神经网络研究多集中在基于现有的风速时间序列对未来时间段内风速进行预测，或对数值天气预报风速进行数据校核和订正，提高风功率短期预报精确度。基于上述研究，可以假设缺测数据为未来时段内需预测的数据，以此来探讨BP神经网络模型应用于风电场测风数据插补工作中的可行性。

本文基于测风塔50m高度层缺测数据，采用训练后的BP神经网络模型、风速的线性关系和非线性关系三种方法进行插补分析，结果表明BP神经网络计算值插补风速带来的误差最小。本研究为风电场缺测数据进行插补提供了一定的参考依据。

测风塔概况

本文所选某风电场的测风塔高度为70m，分为3个测风层，分别为30m、50m、70m，各测风层均安装风速仪，其中30m、70m测风层还安装有风向仪。为简化计算过程，选取该测风塔50m高度在2009年6月15日3：00至2009年6月17日9：00共55个小时数据作为缺测样本数据，进行BP神经网络、线性及非线性三种插补方法误差比较。

BP神经网络模拟训练

一、工作原理

BP（Error Back Propagation）神经网络是采用误差反向传播作为学习算法的前馈网络，通常由输入层、隐含层和输出层构成。层与层之间的神经元采用全互连的连接方式，通过相应的网络权函数相互连接；每层内的神经元之间没有连接。输入层和输出层分别只有一层，隐含层可以为一层或多层，但单隐含层最为普遍，其拓扑结构如图1所示。

图1 三层BP神经网络图

神经元的输入向量为X＝（x0,x1,x2,L,xi,L ,xn）T，其中x0＝－1，可为隐含层神经元引入阈值；神经元隐含层输出为Y＝（y0,y1,y2,L,yj,L ,yn）T，其中y0＝－1，可为输出层神经元引入阈值；神经元输出向量为O＝（o1,o2,L,ok,L ,ol）T，期望输出向量为D＝（d1,d2,L,dk,L ,dl）T；神经元输入层到隐含层的权值用V＝（V1,V2,L,Vj,L ,Vm）来表示，其中列向量为隐含层第j个神经元对应的权向量；神经元隐含层到输出层的权值用W＝（W1,W2,L,Wk,L ,Wl）来表示；列向量Vk为神经元隐含层第k个神经元对应的权向量。

对于输出层，存在：

对于隐含层，存在：

在式（1）和（3）中，激活函数f（x）均为单极性Sigmoid函数：

f（x）具有连续、可导的特点，其导数为：

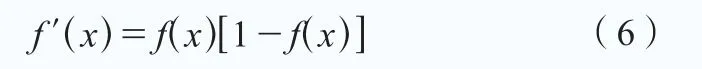
二、风速BP神经网络的训练

依据BP神经网络方法，首先建立50m风速（V50）与70m风速（V70）、30m风速（V30）的表达式，即V50＝ψ（V70,V30）。由于ψ为复杂的非线性函数，要确定其表达式存在相当大的困难或根本无法表达，而人工神经网络模型是一种能模拟非线性输入输出关系的有效工具。将V70和V30作为网络输入层神经元，V50作为网络输出层神经元，来建立V50的BP神经网络模型，如图2所示。

将50m高度的风速实测值与BP神经网络模型训练得到的结果进行对比，结果如图3所示。可以看出BP神经网络模型结果与实测值变化趋势基本一致，其平均相对误差仅为9.3%，由此可得出该BP神经网络模型训练结果良好。

线性和非线性相关性分析

采用线性关系插补，70 m和50 m高度风速数据的线性相关关系如图4所示。线性相关系数R为0.987，大于0.8，两组数据相关性良好，线性相关方程为：y＝0.9166x－0.014。

采用非线性关系插补，以70m和50m高度段的风速数据进行非线性分析，两组数据的非线性相关关系如图4所示。在满足运算精度同时减少计算复杂度的前提下，采用四次多项式拟合，非线性相关系数R为0.988，大于0.8，两组数据相关性良好。非线性相关方程为：y＝－0.00022x4＋0.00765x3－0.07775x2＋1.151x－0.0625。

图2 50m风速BP神经网络结构图

图3 50m高度风速实测值与BP网络计算值

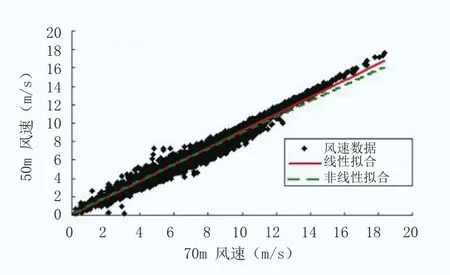
图4 70m和50m高度风速的线性与非线性相关关系

三种插补方法误差分析

将三种插补方式与实测值进行对比，结果如表1和图5所示。

根据计算结果可以得出，BP神经网络计算值的误差绝对值平均值和误差平方和最小，分别为0.35m/s和10.45；非线性计算值次之，分别为0.36m/s和10.52；线性计算值最大，分别为0.49m/s和18.14。通过误差分析结果，认为BP神经网络计算值插补风速带来的误差最小。

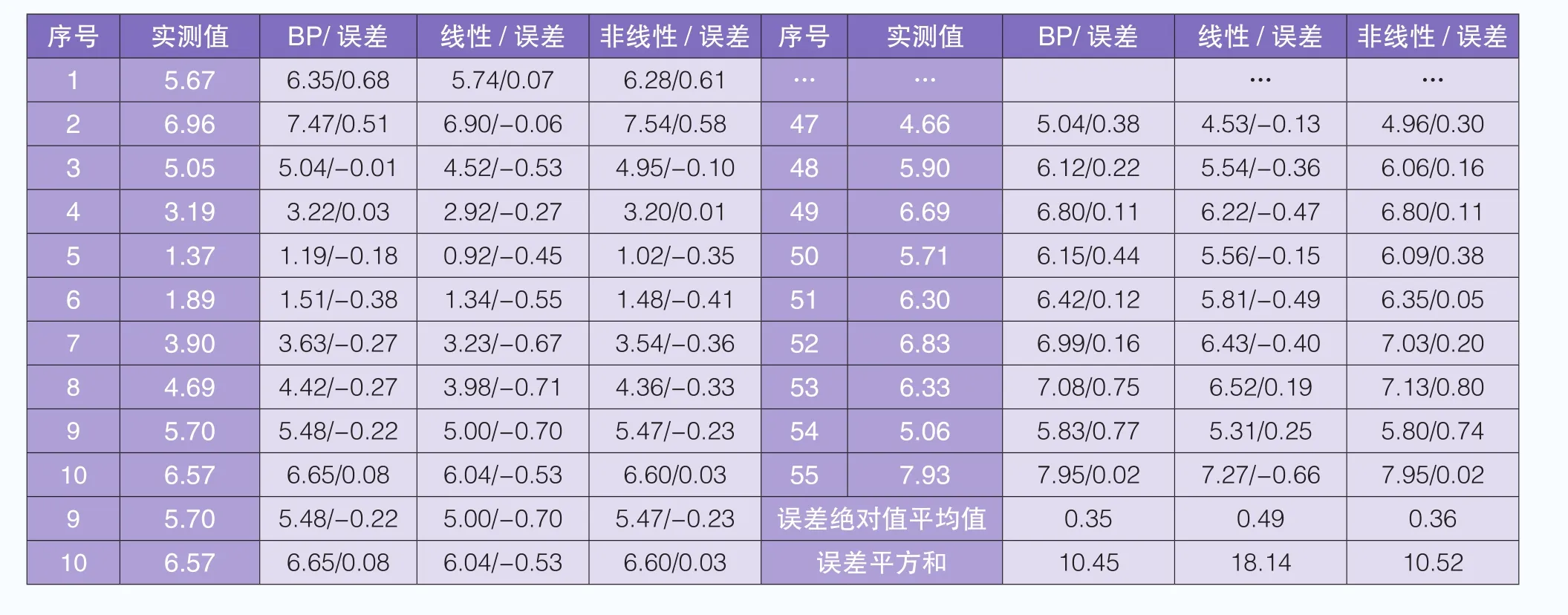
表1 50m高度实测风速数据与三种方法计算值的对比 （m/s）

图5 50m高度风速实测值与三种方法计算值的对比

结语

本文通过对某测风塔70m、50 m和30 m高度的测风数据进行分析，分别通过BP神经网络、线性和非线性相关性分析来对测风塔缺测时段的数据进行插补。所得结论如下：（1）建立了缺测层的BP神经网络模型，利用未缺测层风速数据作为样本来训练BP神经网络模型，训练结果良好，说明采用BP神经网络模型插补数据是可行的。（2）本文的研究结果可以为BP神经网络对风电场缺测数据进行插补提供一定的技术支持。