基于FFT-MA模拟与VFQA算法的纵波模量弹性阻抗随机反演方法

赵 晨,张广智,2,蔡 华,赵 军,张佳佳,2,宋佳杰

(1.中国石油大学(华东),山东青岛266580;2.海洋国家实验室海洋矿产资源评价与探测技术功能实验室,山东青岛266071;3.中海石油(中国)有限公司上海分公司,上海200030)

目前,石油勘探已从简单的构造识别转向复杂构造、薄储层的识别。对于储层识别来说,选取合适的方法估算储层敏感弹性参数具有重要意义。随机地震反演方法以地质统计学为基础,其技术关键在于分析并拟合储层地球物理特性的分布规律,并对不同地球物理参数进行研究,以获得这些参数与地层岩性的关系[1]。地球物理参数可通过经验关系与储层的岩性和流体成分相关联,因此,对于储层描述而言,反演这些参数极有价值[2]。随机模拟地震反演方法有机结合了地震随机反演和地质统计方法,考虑了地下介质的随机特性,因而其反演结果更符合实际地质情况,且分辨率较高[3]。随机反演主要包括随机模拟技术和优化理论。

HASS等[4]最早将序贯高斯模拟技术应用到地震反演中。序贯高斯模拟是经典的条件随机模拟方法,主要用于连续变化的随机模型[5],但该方法存在计算耗时、耗内存等缺点[6-7]。而基于快速傅里叶变换(Fast Fourier Transform,FFT)的谱模拟算法,其计算速度快于常规模拟方法[8],LE RAVALEC等[9]在此理论基础上将快速傅里叶变换与滑动平均模拟相结合,提出了快速傅里叶变换滑动平均(Fast Fourier Transform-Moving Average,FFT-MA)模拟算法,提高了模拟的效率。近几年,王保丽等[10]、孙瑞莹等[11]与YIN等[12]将FFT-MA模拟与优化算法相结合,进行了研究。

METROPOLIS等[13]率先提出了模拟退火(Simulated Annealing,SA)的概念;KIRKPATRICK等[14]利用SA寻找组合问题的最优解;BASU等[15]对SA算法进行了改进,利用依赖于温度的Cauchy或类Cauchy模型产生新解;杨辉等[16]将地球电磁资料与地震资料联合起来,利用非常快速的模拟退火方法(Very Fast Simulated Annealing,VFSA)进行反演,模型试验表明,可提高效率5～10倍。陈华根[17]针对VFSA在修改模型、概率接受、退火策略上做了进一步改进,并对重力和电磁资料进行了联合计算。魏超等[18]参照SA算法提出了量子退火反演的原理和实现流程。量子退火(Quantum Annealing,QA)最优化思想是从模拟退火发展而来的,只是它们的反演机制不同,量子退火是利用量子跃迁隧道效应的机制,而模拟退火是基于热力学的退火原理[19]。2015年,ALULAIW等[20]将基于QA算法的叠前反演方法应用于实际地震资料。

CONNOLLY[21]于1999年提出了弹性阻抗的概念,并给出了弹性阻抗方程。WHITCOMBE[22]对Connolly弹性阻抗方程进行了标准化处理。弹性阻抗反演采用叠前角度部分叠加道集,具有较强的抗噪能力。之后,弹性阻抗反演得到了飞速发展。2016年,张世鑫等[23]提出了两角度弹性阻抗反演技术用以解决大角度部分叠加数据缺失的问题。

反演算法的效率以及反演结果的可靠性是纵波模量估算的关键。本文将FFT-MA模拟与改进后的非常快速的量子退火(Very Fast Quantum Annealing,VFQA)算法相结合,提出了基于FFT-MA模拟与VFQA算法的弹性阻抗随机反演方法,提高了反演的计算效率。VFQA算法借鉴了非常快速的模拟退火算法,通过修改扰动方式及增加记忆功能等措施提高了量子退火算法的收敛速度。在反演过程中,本文由FFT-MA模拟获得多个角度弹性阻抗的先验信息,利用角度叠加数据及正演关系获得似然函数,并添加低频平滑约束信息,提高了反演结果的可靠性。最后给出了理论模型数据和实际地震数据的应用实例。

1 理论和方法

本文提出的基于弹性阻抗随机地震反演的纵波模量估算方法在贝叶斯理论框架下进行,主要分为随机反演理论和弹性阻抗反演理论。

1.1 随机反演理论

本文将FFT-MA模拟和VFQA优化算法相结合,充分利用FFT-MA模拟和VFQA优化算法在计算效率上所具有的优势,提高随机反演的计算效率。关于反演精度问题,利用贝叶斯理论,并引入低频平滑约束信息,来确保反演结果的精度及可靠性。

1.1.1 FFT-MA模拟

FFT-MA与经典随机模拟算法不同之处在于其为一种频率域的谱模拟方法,模拟效率要高于传统的模拟方法。该方法能够分离模拟过程中的随机项和空间结构项,保证空间结构不变且对随机项进行扰动更新,易于结合优化算法对反演问题进行求解[24]。

FFT-MA平均模拟的基本公式为:

(1)

FFT-MA模拟方法是一种非条件模拟方法,在实际应用时应采用克里金方法对模拟结果进行条件化处理,得到条件化FFT-MA算法。为验证FFT-MA的模拟效果,丁龙翔[26]等将条件化的FFT-MA算法和经典的序贯高斯模拟算法进行了对比,发现条件化FFT-MA算法相比序贯高斯模拟方法计算速度提高了十几倍。

1.1.2QA优化算法

优化算法的评价主要通过比较优化算法的精度及效率来确定。对于FFT-MA模拟结果的优化,量子退火算法既保证了优化结果的精度,又能提高优化计算的效率。

量子退火主要利用量子涨落的机制,来完成最优化过程,这是因为量子的隧道效应使得粒子能够穿过比其自身能量高的势垒直接达到较低能量状态[19]。与模拟退火方法相比,量子退火在退火收敛速度和避免陷入局部极小方面有一定优势。

当有外力作用于体系后,系统的Hamilton量H为:

(2)

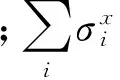
(3)

式中:P为粒子个数;T为退火温度。

相比于传统的模拟退火算法,量子退火算法相当于使用了一种新的接受策略,具体形式如(3)式所示。

1.1.3VFQA算法的改进思路

借鉴VFSA,我们对QA算法进行改进,得到非常快速的量子退火算法(VFQA)。

1.1.3.1 扰动方式

VFSA算法采用了依赖于温度的似Cauchy分布产生新的模型,使扰动步长随温度逐步衰减,加快了算法的收敛速度。同理,我们同样可采用该方法去改进原有的量子退火算法,提高算法的收敛速度,具体形式为:

(4)

式中:mi为未修改模型中的某一参量;mj为修改后模型中的某一参量;[Ai,Bi]为mi的取值范围;T为当前的温度;u为取值[0,1]的随机数。

1.1.3.2 接受准则

接受概率是当前温度下产生的新解可能被接受的概率。参考Metropolis接受准则,改进的接受准则为:

(5)

式中:K为一常数;φ为随温度减小的量。当ΔE≤0且exp{[-(ΔE+Kφ)]/T}>rand(rand为范围为[0,1]的随机数)时,新解可以被接受,否则新解不能被接受。Kφ的引入,使迭代的反演结果在接近模型参数的时候,依旧存在一定的接受概率,使其快速接近最优结果。

1.1.3.3 其它改进措施

在算法中加入记忆功能。设置一个储存空间,并且将每个温度下的最优解保存在该储存空间之中。最后通过比较各个温度下的最优解及最后所得解,找出其中的最小值,作为最终解,这样,可以保证解最优。

1.1.4 目标函数的构建

要利用QA算法对模拟结果进行优化,需构建合适的目标函数。贝叶斯理论框架下的随机反演方法可以更好地融合地震数据和测井信息[27]。利用贝叶斯理论,并引入平滑弹性阻抗约束信息可有效地提高算法的精度及可靠性。

贝叶斯公式具体形式为:

(6)

式中:d表示实际地震记录;p(m)为模型参数m的先验概率密度;p(d|m)为似然函数;p(m|d)为模型参数m的后验概率密度。

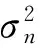
(7)

式中:g表示正演算子;N表示实际地震数据的采样点数量。

假设反演的模型参数满足柯西约束的形式,故模型参数的先验概率可表示为:

(8)

将(7)式、(8)式代入(6)式中,取对数,并加入平滑约束项,即可获得目标函数形式:

(9)

1.2 基于纵波模量的弹性阻抗公式

基于Connolly弹性阻抗公式,宗兆云等[28]改用纵波模量M,剪切模量μ,密度ρ来表示Connolly弹性阻抗方程:

(10)

式中:M0,μ0,ρ0分别表示纵波模量、剪切模量和密度的平均值;参数a,b,c的取值分别为a=sec2θ/2,b=-4ksin2θ,c=1-sec2θ/2。

针对不同角度的地震数据,反演可以得到至少3个不同角度的弹性阻抗体,即:I(θ1),I(θ2),I(θ3)。在角度相同时,各数据点的同种岩性参数[ln(M/M0),ln(μ/μ0)和ln(ρ/ρ0)]所对应的系数值一致,不随时间的变化而改变[29-30]。因此,3个不同角度的弹性阻抗可得到3个不同的公式:

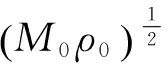
我们利用井旁道弹性阻抗反演结果及测井数据,可以估算出9个系数的值,将其代入公式(11)中,即可得到纵波模量等弹性参数的信息。

利用该弹性阻抗反演方法直接提取纵波模量参数可减小间接反演所带来的累计误差,提高反演的精度。

2 模型测试

利用二维Marmousi2模型中的一部分进行反演测试。图1为弹性阻抗模型、合成地震记录及提取的伪井数据(中角度弹性阻抗)。利用图1c所示的伪井数据通过FFT-MA模拟获得3个角度的弹性阻抗先验信息,之后进行VFQA算法反演,获得3个角度的弹性阻抗反演结果。图2对比了无噪声情况下反演的弹性阻抗与信噪比为3情况下反演的弹性阻抗结果。图3为由图2所示的弹性阻抗体中所提取的纵波模量剖面。

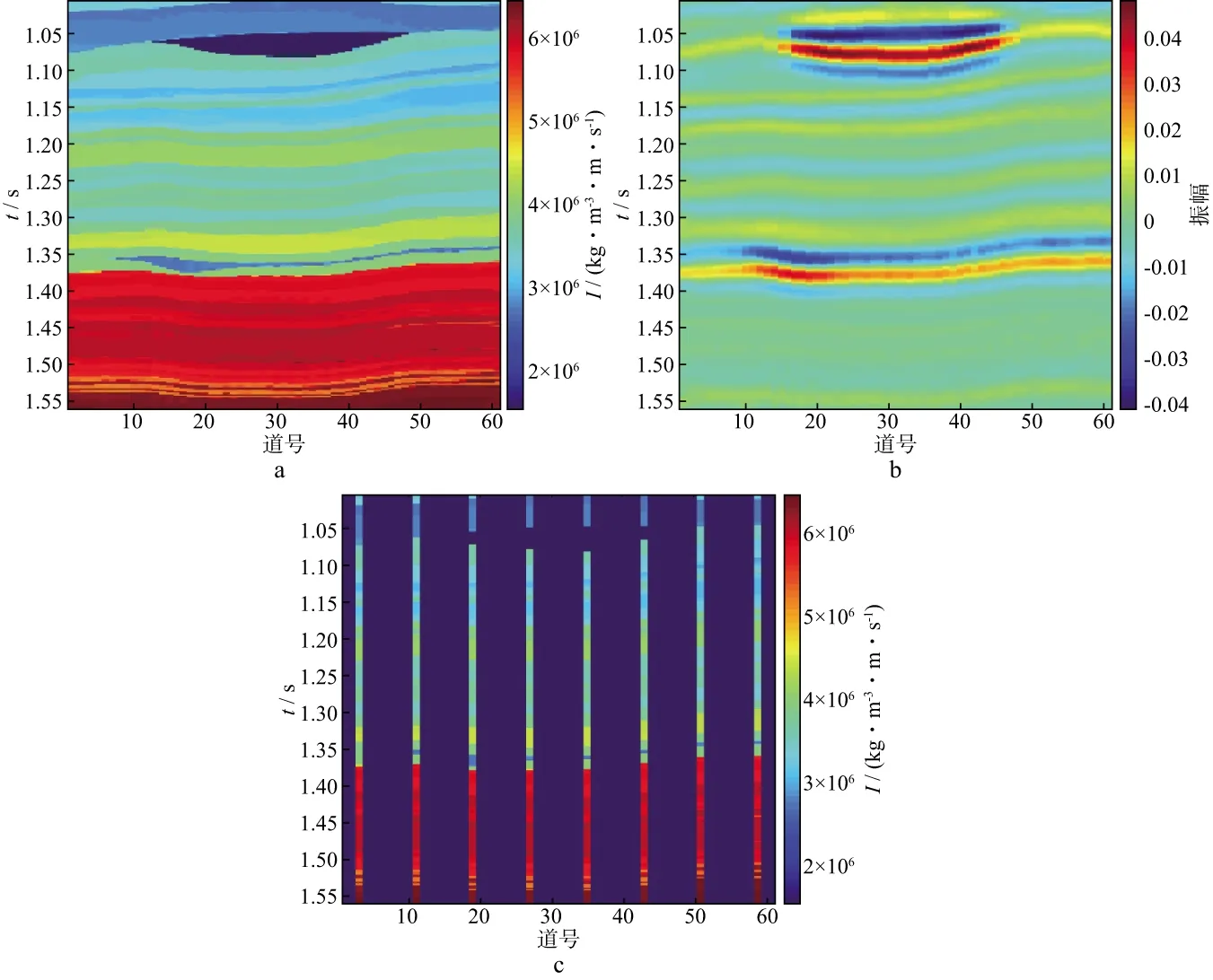
图1 部分Marmous2模型a 弹性阻抗模型数据; b 合成地震记录; c 提取的伪井弹性阻抗数据

从图2和图3中可以看出,弹性阻抗反演结果与

图2 反演得到的弹性阻抗数据a 无噪声时小角度弹性阻抗反演结果; b 信噪比为3时小角度弹性阻抗反演结果; c 无噪声时中角度弹性阻抗反演结果; d 信噪比为3时中角度弹性阻抗反演结果; e 无噪声时大角度弹性阻抗反演结果; f 信噪比为3时大角度弹性阻抗反演结果

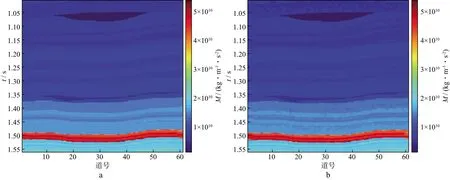
图3 反演得到的纵波模量剖面a 未加噪声; b 信噪比为3

模型数据比较吻合,并且提取的弹性参数比较可信,且存在噪声的情况下,反演的弹性阻抗体和提取的弹性参数依旧比较可靠,均能较好地反映出1.35s附近的薄层,说明基于FFT-MA模拟与VFQA算法的反演方法可行,且具有一定的抗噪性和较高的分辨率。

为了更好地分析反演结果,我们从该二维模型中提取某一道进行分析。对该道数据分别利用非常快速的模拟退火算法(VFSA)、量子退火算法(QA)以及非常快速的量子退火算法(VFQA)进行反演测试。

图4为分别利用3种优化算法(VFSA,QA,VFQA)得到的弹性阻抗与该道模型数据的对比结果(信噪比为3)。图5为从这3种算法反演结果中提取的纵波模量的对比结果。从图4和图5中可以发现,当存在一定噪声时,采用这3种优化算法均能获得与模型数据较为吻合的反演结果,但是QA算法及VFQA算法的精度要略高于VFSA算法。

表1给出了分别利用VFSA,QA以及VFQA进行反演时的计算速度以及精度的对比结果。图6为分别利用VFSA,QA以及VFQA进行反演时接受概率随迭代次数的变化。从表1及图6可以看出,改进后的VFQA算法在迭代150次左右即可收敛,此时相对误差约0.57%,耗时约25.56s,QA算法需迭代600次左右方可收敛,此时误差约2.36%,耗时约60.33s,而VFSA算法须迭代900次左右才能收敛,耗时171.12s。因此,改进后的VFQA相比VFSA以及QA更有优势。

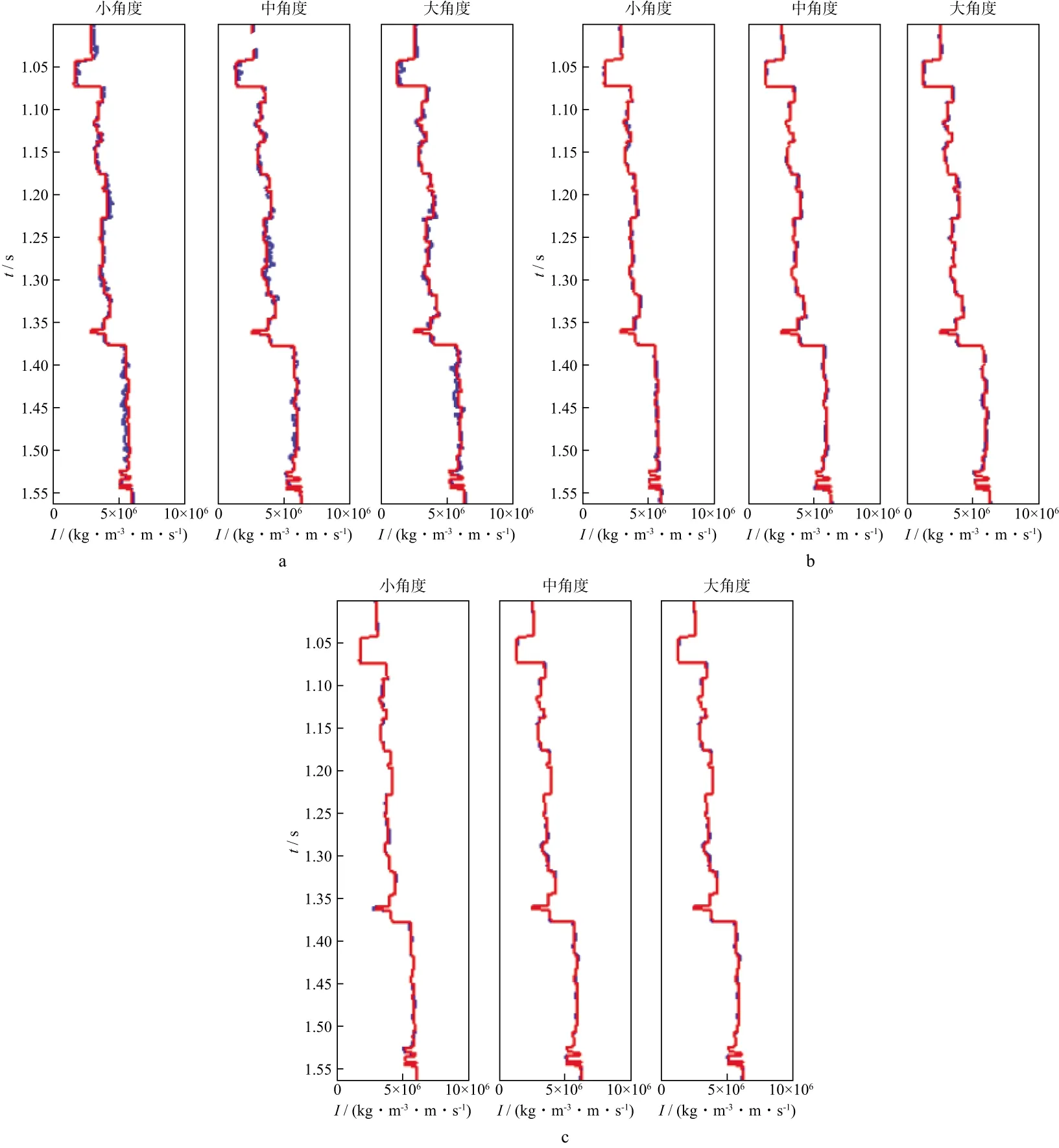
图4 不同反演方法得到的弹性阻抗(红线表示模型数据,蓝线表示反演结果)a VFSA; b QA; c VFQA

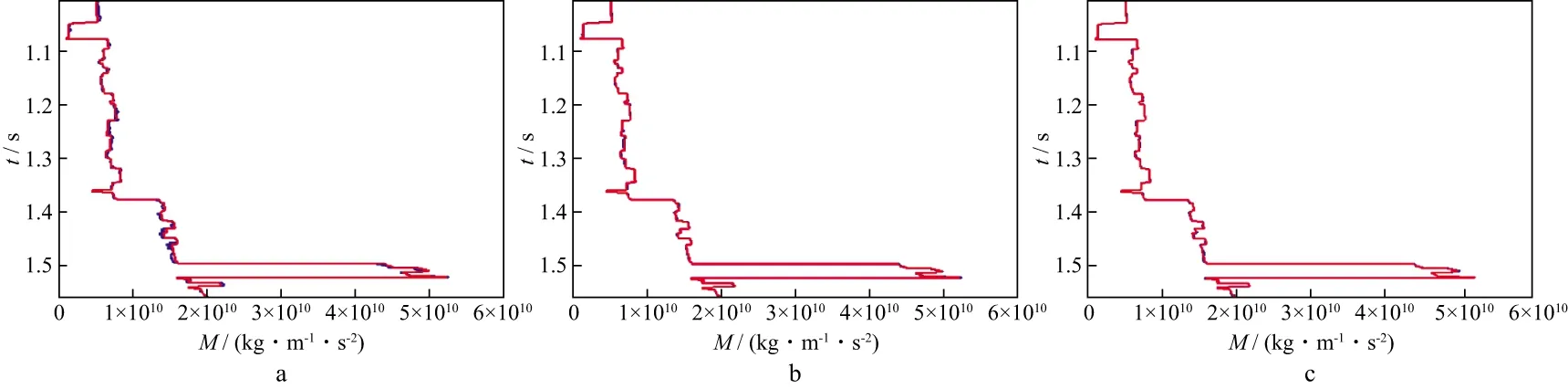
图5 不同反演方法得到的纵波模量(红线表示模型数据,蓝线表示反演结果)a VFSA; b QA; c VFQA

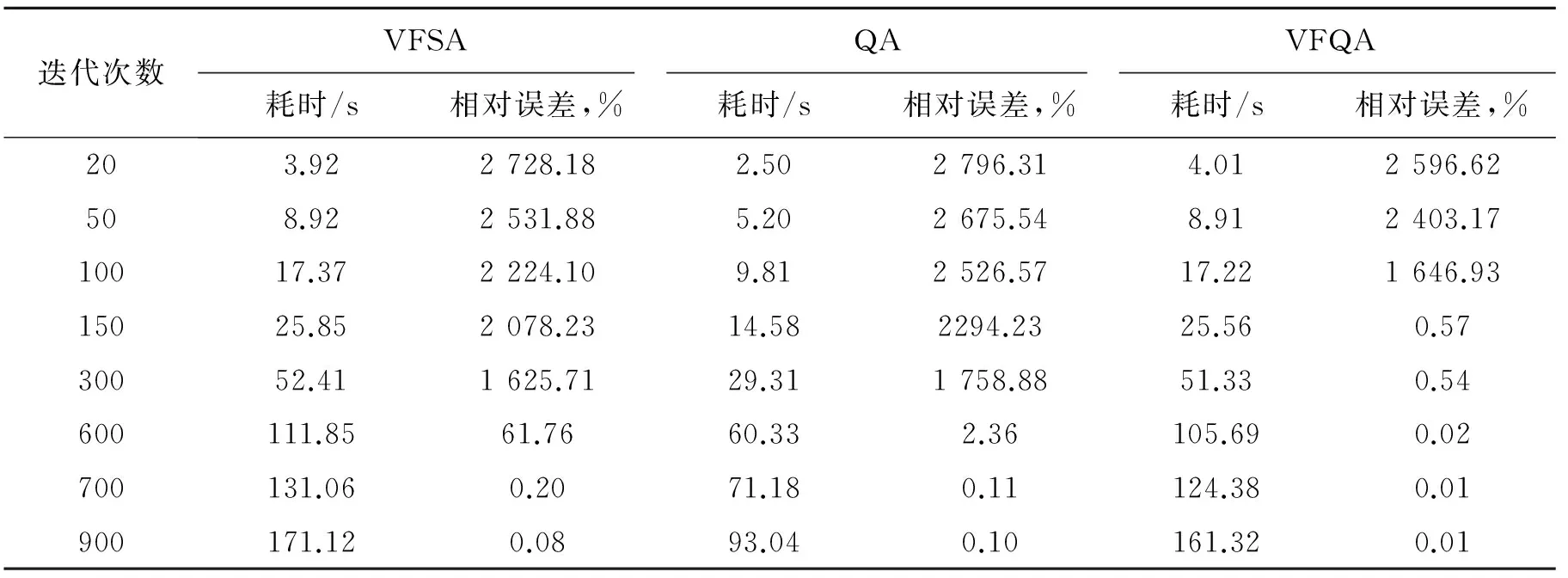
表1 3种算法的计算效率以及精度

图6 不同反演方法接受概率随迭代次数的变化a VFSA; b QA; c VFQA

3 实际数据分析

实际地震数据来自于国内东部油田某工区。为了进行弹性阻抗反演,将叠前地震数据分成3个角度部分叠加数据(小角度:4°～20°,中角度:16°～32°,大角度:28°～44°),地震资料的垂向采样率为0.002s,时间深度为2.344～2.650s。从该工区3个角度叠加数据中提取3个子波,利用井数据及确定性反演的结果通过FFT-MA模拟获得先验信息,之后利用改进后的VFQA算法进行反演。

图7分别是小角度、中角度、大角度弹性阻抗的反演结果。图8为提取的纵波模量剖面。从图7和图8可以看出,弹性阻抗反演结果和所提取的纵波模量剖面与井数据吻合较好,且时间深度在2.55s与2.58s附近的2个较薄的油层在反演剖面上有较好的显示。

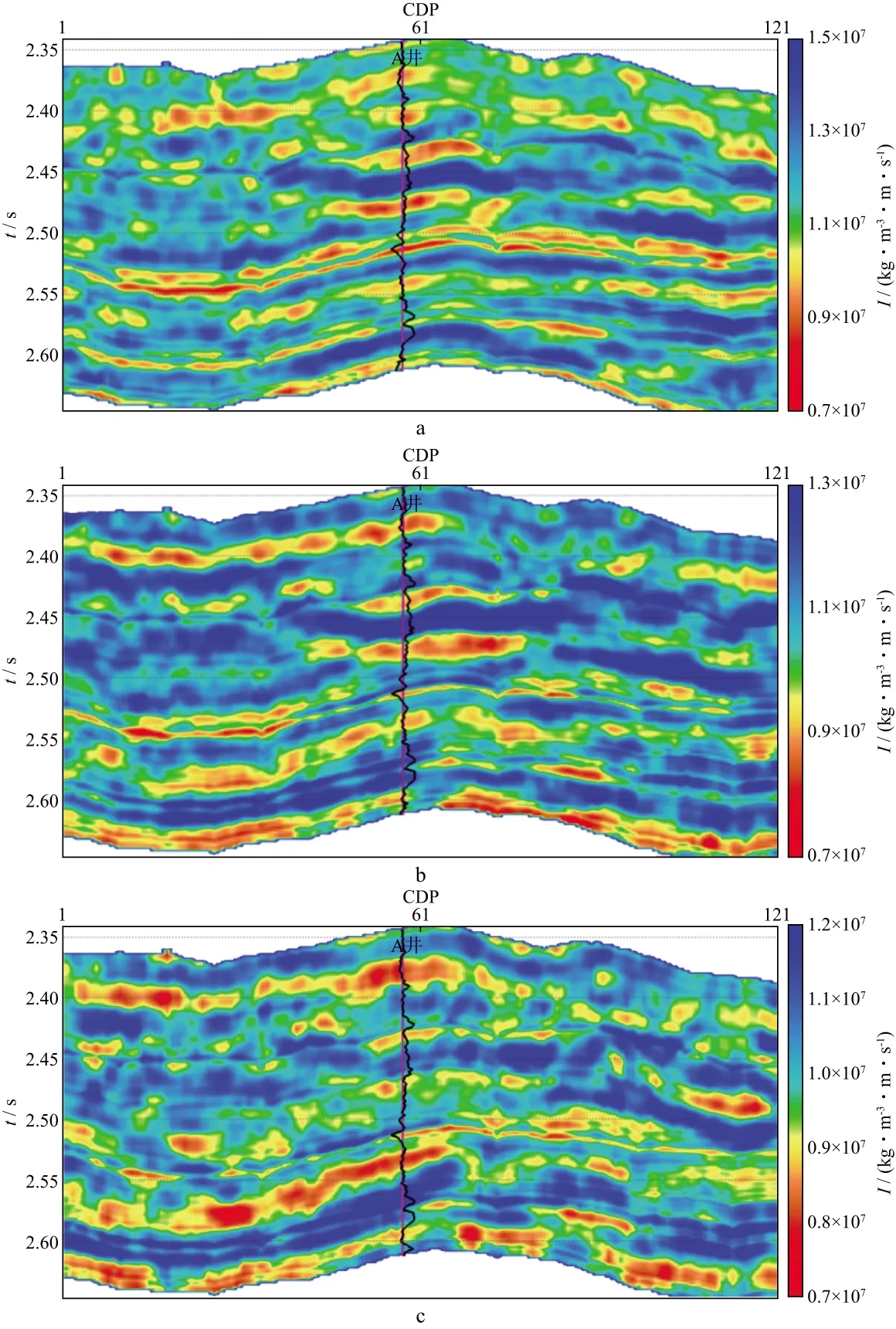
图7 实际地震数据弹性阻抗的反演结果a 小角度; b 中角度; c 大角度

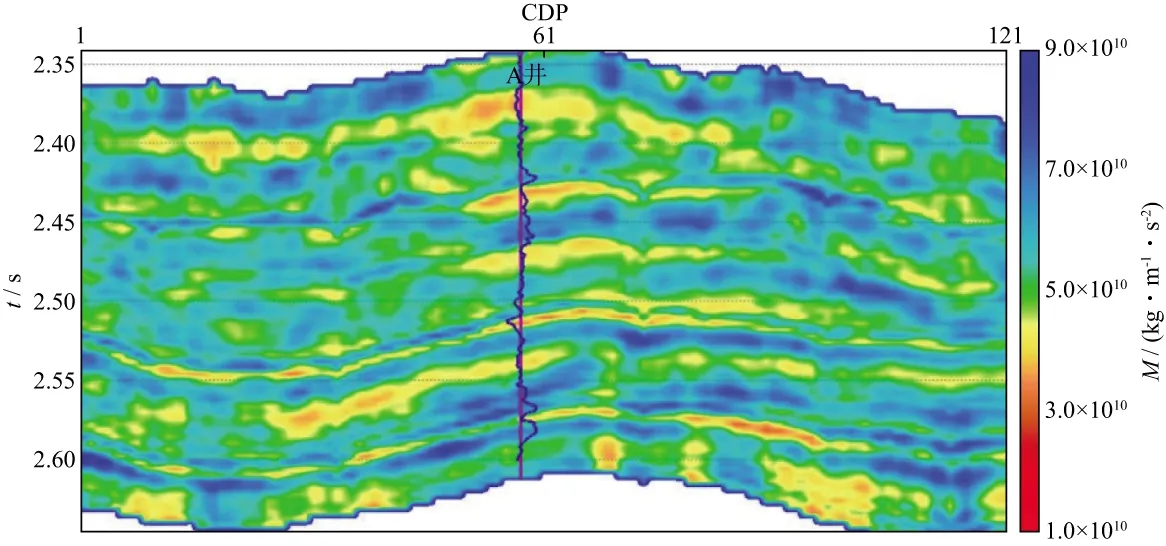
图8 提取的纵波模量剖面

图9为井旁道中角度弹性阻抗和纵波模量的反演结果与实际井数据的对比结果以及中角度弹性阻抗所合成的地震记录与实际地震记录的对比结果。从图9可以看出,井旁道处反演结果所合成的地震记录与实际地震记录吻合较好,而井旁道反演结果虽然与实际井数据并未完全吻合(这是由于地震中存在噪声的影响),但趋势及值域范围基本一致。

为了验证反演的效果,以中角度弹性阻抗反演为例来说明。图10a为中角度部分角度叠加剖面,图10b 为中角度弹性阻抗反演合成地震记录剖面。可以看出,反演结果所合成的地震剖面(图10b)与实际地震记录(图10a)较为接近,验证了该反演方法在实际数据中的可行性。

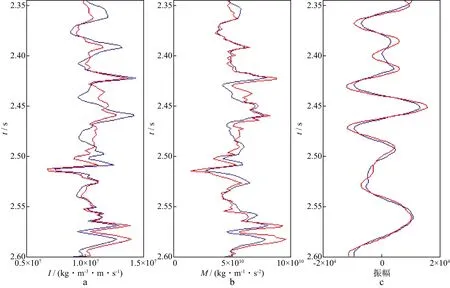
图9 井旁道中角度弹性阻抗(a)、纵波模量(b)的反演结果与实际井数据的对比结果以及中角度弹性阻抗所合成的地震记录与实际地震记录的对比结果(c)(红线表示模型数据,蓝线表示反演结果)

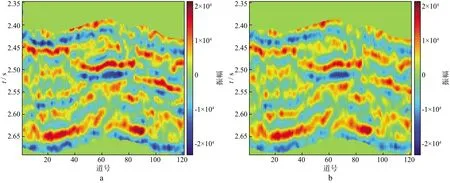
图10 实际地震记录与反演结果所合成的地震记录的对比a 中角度部分角度叠加剖面; b 中角度弹性阻抗反演合成地震剖面

4 结论

纵波模量是储层识别中较为重要的弹性参数。本文提出了基于FFT-MA模拟与VFQA弹性阻抗随机反演方法。利用FFT-MA模拟获得先验信息,正演关系和地震数据构建似然函数,并引入弹性阻抗平滑约束信息,提高了算法的分辨率和可靠性,利用VFSA思路改进QA,提高了计算效率。模型测试结果与实际数据的反演结果表明,该反演方法能够有效获得纵波模量参数,且有较高的分辨率。

[1] 李宁.基于模拟退火的地质统计学反演方法研究[D].青岛:中国石油大学(华东),2013

LI N.The study of geostatistics inversion based on simulated annealing method [D].Qingdao:China University of Petroleum(East China),2013

[2] 王延光.储层地震反演方法以及应用中的关键问题与对策[J].石油物探,2002,41(3):299-303

WANG Y G.Seismic reservoir inversion algorithm and the key problems and policies in its application[J].Geophysical Prospecting for Petroleum,2002,41(3):299-303

[3] 张广智,潘新朋,孙昌路,等.纵横波联合叠前自适应MCMC反演方法[J].石油地球物理勘探,2016,51(5):938-946

ZHANG G Z,PAN X P,SUN C L,et al.PP- & PS-wave prestack nonlinear inversion based on adaptive MCMC algorithm[J].Oil Geophysical Prospecting,2016,51(5):938-946

[4] HAAS A,DUBRULE O.Geostatistical invrsion-a sequential method of stochastic reservoir modelling constrained by seismic data[J].First Break,1994,12(11):561-569

[5] 潘昱洁,李大卫,杨锴.确定性反演和随机反演对井约束条件的需求分析[J].石油物探,2011,50(4):345-349

PAN Y J,LI D W,YANG K.The demand analysis of the constraint condition for the deterministic inversion and stochastic inversion[J].Geophysical Prospecting for Petroleum,2011,50(4):345-349

[6] 王保丽,印兴耀,丁龙翔,等.基于FFT-MA谱模拟的快速随机反演方法研究[J].地球物理学报,2015,58(2):664-673

WANG B L,YIN X Y,DING L X,et al.Study of fast stochastic inversion based on FFT-MA spectrum simulation [J].Chinese Journal of Geophysics,2015,58(2):664-673

[7] SUN R Y,YIN X Y,WANG B L,et al.Simultaneous inversion of petrophysical parameters based on Metropolis sampling algorithm[J].Expanded Abstracts of 84thAnnual Internat SEG Mtg,2014:2611-2615

[8] FRANCIS A.Limitations of deterministic and advantages of stochastic seismic inversion[J].CSEG Recorder,2005,30(1):5-11

[9] LE RAVALEC M,NOETINGER B,HU L Y.The FFT moving average(FFT-MA)generator:an efficient numerical method for generating and conditioning Gaussian simulations[J].Mathematical Geology,2000,32(6):701-723

[10] 王保丽,孙瑞莹,印兴耀,等.基于Metropolis抽样的非线性反演方法[J].石油地球物理勘探,2015,50(1):111-117

WANG B L,SUN R Y,YIN X Y,et al.Nonlinear inversion based on Metropolis sampling algorithm[J].Oil Geophysical Prospecting,2015,50(1):111-117

[11] 孙瑞莹,印兴耀,王保丽,等.基于Metropolis抽样的弹性阻抗随机反演[J].物探与化探,2015,39(1):203-210

SUN R Y,YIN X Y,WANG B L,et al.Stochastic inversion of elastic impedance based on Metropolis sampling algorithm [J].Geophysical and Geochemical Exploration,2015,39(1):203-210

[12] YIN X Y,SUN R Y,WANG B L,et al.Simultaneous inversion of petrophysical parameters based on geostatistical a priori information[J].Applied Geophysics,2014,11(3):311-320

[13] METROPOLIS N,ROSENBLUTH A,ROSENBLUTH M,et a1.Equation of state calculations by fast computing machines[J].Journal of Chemical Physics,1953,21(6):1087-1092

[14] KIRKPATRICK S,GELATT C D,VECCHI M P.Optimization by simulated annealing[J].Sciences,1983,220(4598):671-680

[15] BASU A,FRAZER L.Rapid determination of the critical temperature in simulated annealing inversion[J].Science,1990,249(4975):1409-1412

[16] 杨辉,王家林,吴健生,等.大地电磁与地震资料仿真退火约束联合反演[J].地球物理学报,2002,45(5):723-734

YANG H,WANG J L,WU J S,et al.Constrained joint inversion of magnetotelluric and seismic data using simulated annealing algorithm[J].Chinese Journal of Geophysics,2002,45(5):723-734

[17] 陈华根.基于GIS技术的大地电磁-重力模拟退火联合反演研究[D].上海:同济大学,2001

CHEN H G.GIS based joint inversion of magnetotelluric and gravity data using simulated annealing algorithm[D].Shanghai:Tongji University,2001

[18] 魏超,李小凡,张美根.量子退火最优化与地球物理反演方法[J].地球物理学进展,2007,22(3):785-789

WEI C,LI X F,ZHANG M G.Quantum annealing optimization and geophysical inverse methods[J].Progress in Geophysics,2007,22(3):785-789

[19] 魏超,朱培民,王家映.量子退火反演的原理和实现[J].地球物理学报,2006,49(2):577-583

WEI C,ZHU P M,WANG J Y.Quantum annealing inversion and its implementation[J].Chinese Journal of Geophysics,2006,49(2):577-583

[20] ALULAIW B,SEN M K.Prestack seismic inversion by quantum annealing:application to Cana field[J].Expanded Abstracts of 85thAnnual Internat SEG Mtg,2015:3507-3511

[21] CONNOLLY P.Elastic impedance[J].The Leading Edge,1999,18(4):438-452

[22] WHITCOMBE D N.Elastic impedance normalization[J].Geophysics,2002,67(1):60-62

[23] 张世鑫,韩文明,杜向东,等.两角度弹性阻抗反演技术在Albert湖盆非固结砂岩储层预测中的应用[J].石油物探,2016,55(5):746-753

ZHANG S X,HAN W M,DU X D,et al.Unconsolidated sand reservoir prediction in Albert Lake Basin using two angle elastic impedance inversion technique[J].Geophysical Prospecting for Petroleum,2016,55(5):746-753

[24] 印兴耀,刘婵娟,王保丽.基于混合遗传算法的叠前随机反演方法[J].中国石油大学学报(自然科学版),2017,41(4):65-70

YIN X Y,LIU C J,WANG B L.Prestack Stochastic inversion based on hybrid genetic algorithm[J].Journal of China University of Petroleum(Edition of Natural Science),2017,41(4):65-70

[25] 孙瑞莹.先验信息构建与地震随机反演方法研究[D].青岛:中国石油大学,2015

SUN R Y.Study of the priori information construction and seismic stochastic inversion method[D].Qingdao:China University of Petroleum,2015

[26] 丁龙翔.高分辨率随机反演方法研究[D].青岛:中国石油大学,2013

DING L X.Study on high resolution stochastic inversion method[D].Qingdao:China University of Petroleum,2013

[27] 印兴耀,孙瑞莹,张广智,等.基于分形高频初始模型和低频先验信息的物性参数随机反演[J].石油物探,2014,53(5):537-544

YIN X Y,SUN R Y,ZHANG G Z,et al.Stochastic inversion of reservoir physical property parameters based on high-frequency initial model from fractal and low-frequency prior information[J].Geophysical Prospecting for Petroleum,2014,53(5):537-544

[28] 宗兆云,印兴耀,吴国忱.基于叠前地震纵横波模量直接反演的流体检测方法[J].地球物理学报,2012,55(1):284-292

ZONG Z Y,YIN X Y,WU G C.Fluid identification method based on compressional and shear modulus direct inversion[J].Chinese Journal of Geophysics,2012,55(1):284-292

[29] SUN R Y,YIN X Y,TAN X,et al.Stochastic inversion of elastic impedance based on Metropolis sampling algorithm[J].Geophysical & Geochemical Exploration,2015,39(1):203-210

[30] 王保丽,印兴耀,张繁昌.弹性阻抗反演及应用研究[J].地球物理学进展,2005,20(1):89-92

WANG B L,YIN X Y,ZHANG F C.Elastic impedance inversion and its application[J].Progress in Geophysics,2005,20(1):89-92