时频域稀疏优化谐波噪声压制方法及其在准噶尔盆地高密度地震勘探中的应用
2018-02-27刘宏杰毛海波师振盛
罗 勇,刘宏杰,毛海波,蒋 立,师振盛
(1.中国石油天然气股份有限公司新疆油田分公司勘探开发研究院地球物理研究所,新疆乌鲁木齐830013;2.西安交通大学电子与信息工程学院,陕西西安710049)
目前全球可控震源采集工作量占陆地勘探总量的70%左右,但国内可控震源采集比例相对较小,仅为29%左右[1]。无论是从经济效益的角度,还是从环保与安全的角度,可控震源必将成为未来国内外陆上地震勘探的主要震源。相比传统的炸药震源,近年来研发成功的低频可控震源可获得低至1.5Hz左右的有效波成分,大大提高了地震反演的精度与成功率,为地震全波形反演(FWI)提供了有效的低频成分。谐波噪声是由可控震源自身机械液压系统的非线性以及可控震源的基板与地面耦合的非线性导致传播到大地的地面力信号发生谐波畸变而产生的。两次扫描相隔时间越短,数据受谐波噪声的影响就越大。受到谐波干扰较强的地震记录上,有效信号往往被谐波噪声掩盖,信噪比严重降低,必须对谐波噪声进行压制。考虑计算代价及存储空间等因素,本文重点关注相关后地震记录谐波噪声压制的方法。
遗传算法对谐波噪声的压制具有一定的效果[2],但是该算法搜寻全局最优解的运算量巨大,难以应用于工业生产。模拟退火法对谐波噪声也有一定的压制作用[3],能够将掩藏在谐波噪声中的弱反射信号提取出来,但是搜寻全局最优解导致算法运算量较大,计算效率低,难以适应海量地震资料处理。SICKING等[4]基于相关后数据、地面力信号和每一炮数据的初至时间,将力信号分解成为基波与谐波成分,通过设计合理的滤波器估计本炮数据的谐波噪声,并从上一炮数据中去除本炮数据估计的谐波噪声。该方法必须从没有受到谐波干扰的最后一炮记录开始串行处理,无法处理单炮。此外,为了避免对有效信号造成损伤,在从上一炮数据中减去本炮对上一炮产生的谐波干扰的过程中,必须确定本炮谐波干扰在上一炮数据中出现的时间位置。此后,多位学者基于地面力信号分解发展了反褶积、反相关等谐波噪声压制方法[5-8]。然而,由于地层介质的不均匀性以及衰减吸收作用,不同传播路径的地面力信号波形会发生变化,而上述方法均假设地面力信号保持不变,因而其应用效果会受到明显影响。2011年,钟飞等[9]利用希尔伯特-黄(Hilbert-Huang)变换在时频域将高次谐波压制后,再将所有的内蕴模式函数(intrinsic mode function,IMF)叠加,得到去除谐波后的信号。该方法对谐波噪声有一定的压制作用,但由于谐波噪声存在宽频特性,会同时出现在多个IMF中,可能与有效信号交叠,降低了该方法的适用性。伍建等[10]假设谐波噪声与扫描信号成线性关系,结合各次谐波噪声的能量比例关系,计算得到谐波噪声。CASTOR等[11]通过反馈系统改进震源来降低谐波噪声,该方法能够有效压制谐波噪声低频成分,但是对谐波噪声的高频成分压制效果不明显。李振春等[1]与曲英铭等[12]对谐波噪声产生的机理及特征进行了系统研究和分析,在此基础上采用自适应匹配滤波方法压制谐波干扰,在一定程度上解决了地面力信号记录不准确、大地介质对基波信号及谐波干扰衰减不同所造成的谐波预测不准确问题。
时频域稀疏优化的谐波噪声压制方法是近年来发展起来的一种保真去噪算法[13],该方法基于炮集相关后数据中有效信号与谐波噪声在时频分布特征上的差异分离谐波干扰。本文首先介绍了时频域稀疏优化谐波噪声压制方法的基本原理,然后给出了稀疏表示字典主要参数的确定方法,最后通过准噶尔盆地玛湖地区实际三维地震资料处理,验证了本文方法的有效性。
1 方法原理
1.1 谐波噪声压制
将可控震源滑动扫描采集的数据相关后原始单炮记录表示为有效信号成分(包括反射体波及瑞雷面波)和谐波噪声两种信号分量的线性叠加,即:
(1)
式中:Ss为有效信号;Sh为谐波噪声;N为高斯分布白噪声。
(1)式中引入加性高斯白噪声,描述了数据采集过程中设备热噪声和其它随机干扰等对数据采集的影响。如果信号在某个变换中可以由少数几个基本原子的线性组合表示,我们就说信号在这个变换中是稀疏的。如果信号在某种变换中能够获得稀疏表示,那么就可以从噪声背景或者不完备采样数据中得到高精度恢复(即压缩感知理论)[14]。
对于复杂的地震信号,仅用一个变换并不能对其进行稀疏表示。如果能将多种信号表示工具联合起来组成强大的波形字典,则可以对复杂的实际信号进行稀疏表示,这就是STARCK等[15]提出的形态成分分析方法的基本思想。针对谐波噪声压制问题,基于形态成分分析方法从地震记录中分离有效信号和谐波噪声需满足如下两点要求:①稀疏变换Φs能稀疏表示有效信号,但是不能稀疏表示谐波干扰;②稀疏变换Φh能稀疏表示谐波噪声,但是不能稀疏表示有效信号。通过求解如下最优化问题实现有效信号和谐波噪声的高精度分离:
(2)
式中:Xs表示有效信号在稀疏变换Φs下的系数向量;Xh表示谐波噪声在稀疏变换Φh下的系数向量;ε表示重构数据的误差阈值,作为约束项使得优化问题可以在随机干扰以及数据不完备的情况下仍然能够取得合理的稀疏解。求解(2)式,即可从炮集记录中分离出谐波噪声干扰。
1.2 稀疏表示字典主要参数的确定
从上述分析可以看出,时频域稀疏优化谐波噪声压制方法的核心是稀疏表示字典的选择或构造。自MORLET等[16]、GOUPILLAUD等[17]提出连续小波变换的概念以来,Morlet小波函数作为稀疏表示地震信号的主要工具之一已得到广泛应用[18]。本文利用连续小波变换稀疏表示有效信号[13](包括体波及面波),即将Morlet小波作为波形字典Φs。考虑谐波干扰在时频域表现为近似线性分布的特征,本文选择Chirplet变换[13,19]原子作为稀疏表示谐波干扰噪声的波形字典Φh。连续小波变换如公式(3)所示,Chirplet变换如公式(4)~公式(6)所示,图1给出了Morlet小波函数(实部)和Chiplet原子示意图。
(3)
式中:a表示尺度因子;x(t)表示待分析信号;Ψ(t)表示小波母函数。
(4)
式中:x(t)表示待分析信号;f为频率;a为尺度因子;c为时间上的线性调频率;d为频率上的线性调频率;h(t,f,a,c,d)为Chirplet变换的核函数。
(5)
式中:g(t)为高斯函数,其表达式如下。
(6)
公式(2)能否成功地从实际地震信号中分离出谐波噪声,字典原子的主要参数选择至关重要。可控震源滑动扫描频率可以确定小波变换中Morlet小波函数尺度因子a的范围。Chirplet原子中参数c,d及v的选择,需使得Chirplet原子的时频分布与谐波噪声干扰主要能量的时频分布斜率近似一致。另外Chirplet变换中尺度因子a的范围由谐波干扰的频率分布范围大致确定。

图1 用于谐波噪声压制的稀疏表示字典原子a Morlet小波函数(实部); b Chirplet原子
2 实际资料应用
准噶尔盆地玛湖地区构造相对简单,主要勘探目的层基本为东南倾的平缓单斜,局部发育由坡折带引起的低幅度构造,断裂较少。根据工区地震地质条件及地质任务要求,结合近年来高密度地震勘探实施的成功经验,采用可控震源滑动扫描采集技术进行了高密度宽方位三维采集。可控震源滑动扫描参数分别为:扫描频率3~90Hz,扫描时间16s,滑动时间11s。分析三维工区原始单炮记录可知,该区谐波干扰对原始数据的信噪比影响较大,部分单炮中谐波已经影响到目的层,且谐波噪声在30~75Hz高频范围内出现,在此频率范围内信号和噪声同时存在。
本文将时频域稀疏优化谐波噪声压制方法应用于该区三维典型单炮记录去噪处理,并将其与工业界常用的FDNAT方法进行了对比。FDNAT方法通过频变和时变振幅门槛值检测和压制不同频率范围和不同时间的异常能量噪声。
2.1 单炮记录去噪处理
图2a为玛湖地区采用滑动扫描采集方式得到的相关后三维原始单炮记录。该记录共396道,每道3000个采样点,采样间隔2ms,可以看出剖面上存在明显的谐波干扰噪声(剖面右半部分)。该炮数据中深部有效波横向连续性较好,利于分析对比方法的保真性。图2b为采用FDNAT方法压制谐波噪声后的结果,图2c为采用时频域稀疏优化方法压制谐波噪声后的结果。可以看出两种方法均明显压制了谐波噪声干扰。图2d和图2e分别是FDNAT方法和时频域稀疏优化方法分离出的谐波噪声。可以看出,时频域稀疏优化方法分离出的噪声剖面中几乎没有有效信号的能量残留。FDNAT方法在压制谐波噪声的同时,对面波噪声也有显著的压制作用,然而该方法对有效波的损伤明显。图3a至图3e分别为图2中红框所示部分局部放大显示结果,可以进一步对比出时频域稀疏优化方法与FDNAT方法压制谐波干扰的异同。
图4为图2a至图2c中第256道数据局部对比结果,可以看出时频域稀疏优化方法压制谐波噪声后,对有效信号具有良好的保真能力,尤其是对中深层的弱信号(图中黑色椭圆所示位置)。图5为图4对应数据的归一化Fourier振幅谱,其中蓝色、绿色、红色细实线分别对应原始数据、FDNAT方法去噪后得到的有效信号、时频域稀疏优化方法去噪后得到的有效信号。从原始数据归一化振幅谱中能清晰地观察到谐波噪声对有效信号的影响,时频域稀疏优化方法和FDNAT方法均明显压制了谐波噪声干扰,但FDNAT方法得到的有效信号中还存在较明显的高频谐波噪声能量残留。另外,时频域稀疏优化方法对有效信号的低频保持要优于FDNAT方法,这为后续的地震数据叠前、叠后反演等奠定了良好的基础。

图2 三维典型单炮记录处理对比a 原始单炮记录; b FDNAT方法压制谐波噪声的结果; c 时频域稀疏优化方法压制谐波噪声的结果; d FDNAT方法分离的噪声; e 时频域稀疏优化方法分离的噪声

图3 图2局部放大显示a 原始单炮记录; b FDNAT方法压制谐波噪声的结果; c 时频域稀疏优化方法压制谐波噪声的结果; d FDNAT方法分离的噪声; e 时频域稀疏优化方法分离的噪声

图4 单炮记录第256道数据对比(局部)
2.2 单炮反褶积对比
反褶积是地震资料处理的必要环节之一,经过噪声压制处理后的地震数据可以通过反褶积处理测试去噪方法对噪声的压制程度,同时可以检验去噪方法对有效信号的保真度。图6a至图6c分别为图2a 至图2c对应的脉冲反褶积结果。对比可见,经反褶积处理后,中高频有效信号的能量抬升明显,同时出现了信噪比下降,其中FDNAT方法信噪比下降明显。图7为图6a至图6c在时窗2~6s中的多道数据平均归一化振幅谱对比结果(图6中红框所示部分)。对比可见,FDNAT方法压制谐波噪声后高频噪声抬升明显,如图7中黄色椭圆处所示,这会给后续的反演及属性分析,尤其是叠前资料处理解释带来不利影响。另外,FDNAT方法使有效信号的主要频段产生了明显的畸变,如图7中黑色椭圆部分所示。说明工业界常用的FDNAT方法虽然可以压制谐波噪声,但是对主要频段的有效信号造成了明显损伤。与FDNAT方法相比,时频域稀疏优化方法在压制谐波噪声的同时具有良好的保真性能。
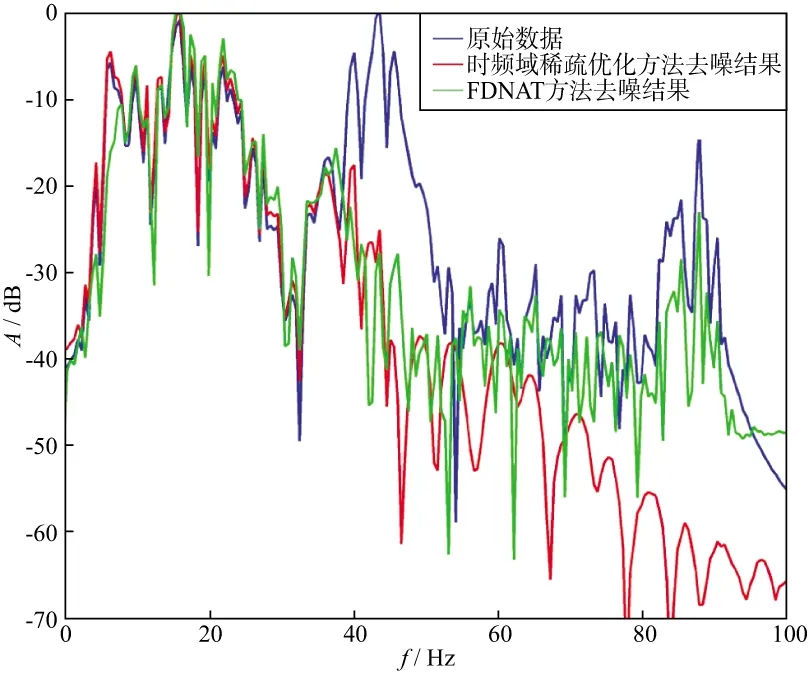
图5 图4对应的归一化振幅谱
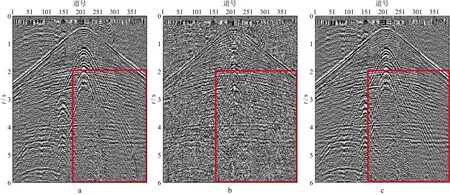
图6 反褶积结果对比a 原始数据; b FDNAT方法压制谐波噪声后; c 时频域稀疏优化方法压制谐波噪声后

图7 图6中2~6s时窗多道数据平均归一化振幅谱
3 结束语
本文通过构造有效信号及谐波干扰噪声的稀疏表示字典,建立基于双波形字典的形态成分分析模型,通过求解该稀疏优化问题可以进行信噪分离和谐波噪声压制。将该时频域稀疏优化方法应用于准噶尔盆地玛湖地区高密度三维典型单炮数据的谐波噪声压制,并与目前工业界常用的FDNAT方法进行了对比,结果表明,时频域稀疏优化方法能在压制谐波噪声的同时,对有效信号具有良好的保真性能。
致谢:感谢西安交通大学电子与信息工程学院陈文超教授提供的基础算法程序及实际资料处理过程中给予的建议和指导。
[1] 李振春,曲英铭,韩文功,等.可控震源两种谐波产生机理与特征研究[J].石油物探,2016,55(2):159-172
LI Z C,QU Y M,HAN W G,et al.Generation mechanism and characteristics of two kinds of harmonic waves for vibroseis[J].Geophysical Prospecting for Petroleum,2016,55(2):159-172
[2] DAL MORO G,SCHOLTZ P,IRANPOUR K.Harmonic noise attenuation for vibroseis data[J].Gruppo Nazionale Di Geofisica Della Terra Solida,2007,3(2):511-513
[3] SHARMA S P,TILDY P,IRANPOUR K,et al.Attenuation of harmonic noise in vibroseis data using simulated annealing[C]∥Geophysical Research Abstracts.Germany:European Geosciences Union,2009:8693
[4] SICKING C,FLEURE T,NELAN S,et al.Slip sweep harmonic noise rejection on correlated shot data[J].Expanded Abstracts of 79thAnnual Internat SEG Mtg,2009:36-40
[5] EL-AAL A E-A K A.Eliminating upper harmonic noise in vibroseis data via numerical simulation[J].Geophysical Journal International,2010,181(3):1499-1509
[6] 曹务祥,闫智慧,邹小燕,等.利用可控震源的力信号压制谐波干扰[J].石油物探,2011,50(1):89-92
CAO W X,YAN Z H,ZOU X Y,et al.Harmonic interference suppressing by force signal of vibroseis[J].Geophysical Prospecting for Petroleum,2011,50(1):89-92
[7] 王宝彬,李合群,赵波,等.滑动扫描地震数据的谐波干扰压制[J].石油地球物理勘探,2013,48(1):37-41
WANG B B,LI H Q,ZHAO B,et al.Harmonic noise removal on vibroseis slip-sweep data[J].Oil Geophysical Prospecting,2013,48(1):37-41
[8] QU S,ZHOU H,ZHANG H,et al.An effective denoising method for removing harmonic distortion in correlated vibroseis data[J].Expanded Abstracts of 84thAnnual Internat SEG Mtg,2014:4284-4288
[9] 钟飞,张伟,钟约先.Hilbert-Huang变换去除可控震源谐波畸变[J].清华大学学报(自然科学版),2011,51(6):862-867
ZHONG F,ZHANG W,ZHONG Y X.Removal of harmonic distortions in vibroseis data using the Hilbert-Huang transformation [J].Journal of Tsinghua University:Science and Technology Edition,2011,51(6):862-867
[10] 伍建,王润秋,魏加明,等.可控震源地震数据谐波滤除方法[J].石油地球物理勘探,2014,49(1):47-52
WU J,WANG R Q,WEI J M,et al.A method for vibroseis data harmonic filtering[J].Oil Geophysical Prospecting,2014,49(1):47-52
[11] CASTOR K,BIANCHI T,WINTER O,et al.Noise reduction in vibroseis source[J].Expanded Abstracts of 84thAnnual Internat SEG Mtg,2014:16-20
[12] 曲英铭,李振春,黄建平,等.自适应匹配预测滤波压制可控震源谐波[J].石油地球物理勘探,2016,51(6):1075-1083
QU Y M,LI Z C,HUANG J P,et al.Vibroseis harmonics suppression based on adaptive matched predictive filtering[J].Oil Geophysical Prospecting,2016,51(6):1075-1083
[13] 陈文超,李祥芳,王伟,等.可控源谐波噪声压制的时频域稀疏优化方法[C]∥中国石油学会.2015 年物探技术研讨会论文集.涿州:石油地球物理勘探编辑部,2015:151-154
CHEN W C,LI X F,WANG W,et al.Sparsity optimized method in time-frequency domain for vibroseis harmonics suppression[C]∥Chinese Petroleum Society.2015 Geophysical Technology Symposium.Zhuo-zhou:Oil Geophysical Prospecting Editorial Office,2015:151-154
[15] STARCK J L,ELAD M,DONOHO D L.Image decomposition via the combination of sparse representations and a variational approach[J].IEEE Transactions on Image Processing,2005,14(10):1570-1582
[16] MORLET J,ARENS G,FOURGEAU E,et al.Wave propagation and sampling theory-part I:complex signal and scattering in multi-layered media[J].Geophysics,1982,47(2):203-221
[17] GOUPILLAUD P L,GROSSMANN A,MORLET J.A simplified view of the cycle-octave and voice representations of seismic signals[J].Expanded Abstracts of 54thAnnual Internat SEG Mtg,1984:379-382
[18] 王西文.地震资料处理和解释中的小波分析方法[M].北京:石油工业出版社,2004:15-20
WANG X W.Wavelet analysis method for seismic data processing and interpretation[M].Beijing:Petroleum industry Press,2004:15-20
[19] MANN S,HAYKIN S.The Chirplet transform:physical considerations[J].IEEE Transactions on Signal Processing,1995,43(11):2745-2761
