跨中受落石冲击的拱形护桥明洞力学响应
2018-02-27王玉锁何俊男
王玉锁, 王 涛, 周 良, 何俊男, 徐 铭
0 引言
我国西部艰险山区的铁路、公路常受危岩落石灾害侵扰,不仅对行车运营造成安全隐患,还对结构造成不同程度破坏。对于危岩落石灾害,除主动防护外,还有被动防护,其中采用拱形明洞和棚洞是主要的刚性被动防护措施[1-2]。通常,拱形明洞为断面与暗挖隧道一致的带仰拱的闭合结构,而棚洞是有平顶的框架结构,二者上部均设有回填土作为缓冲层。从力学角度看,拱形明洞结构承载力要强于由梁、板、柱组成的棚洞结构;从施工角度看,采用拱形结构不一定就比传统棚洞结构施工复杂,有时还由于工序单一而更易于质量控制,且上部拱圈、边墙等为连续浇筑,整体性更好[3-4]。基于此,在桥隧相连段,为保护隧道洞门、道路和桥梁结构,在桥隧相连段一定范围,修建顶部为拱形的明洞结构,以保护隧道洞门和与之相连的桥梁结构,也称为护桥棚洞[5],结构型式如图1所示。
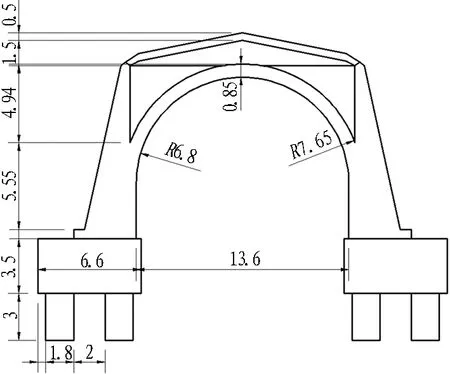
图1 护桥棚洞设计图(单位: m)
Fig. 1 Design sketch of protection arched shed of bridge (unit: m)
图1中上部结构的拱圈、边墙及下部结构的承台、桩基之间均固结,材料为C35钢筋混凝土;上部结构的拱部与耳墙间采用C20混凝土填充到与拱顶平齐,其上夯填土石,最上面为黏土隔水层。
图1所示结构与传统的棚洞及拱形明洞均不相同,而目前研究较多的是落石冲击下钢筋混凝土或柔性棚洞结构的力学响应,主要采用数值模拟方法进行分析[6-9];拱形明洞研究近年来也开始逐渐深入[4,11-12],但针对的是有仰拱的闭合结构。文献[12]开展了与图1类似的结构落石冲击室内模型试验,得出了模型结构不同部位的力学响应特征,但没有考虑下部结构的立柱。
由于图1所示结构复杂,与传统的棚洞及拱形明洞结构特点都不相同,落石冲击下除上部结构外,下部的承台及出露地面的立柱受力,也是以前类似研究没有探讨过的,有必要对结构的受力不利部位及需要加强的关键部位进行全面深入的研究。
本次以图1结构设计为原型,从落石与回填缓冲层相互作用过程入手,进行冲击点位于结构顶部跨中部位、沿不同落石冲击方向下拱形护桥明洞结构整体受力的数值模拟分析,并与冲击前静力平衡状态下的结构受力进行对比分析,明确结构受力的不利部位。
1 数值模型及参数
采用动力有限元软件ANSYS/LS-DYNA,对图1所示护桥明洞在落石冲击下的力学响应进行研究,所建模型如图2所示。

(a) 模型正面
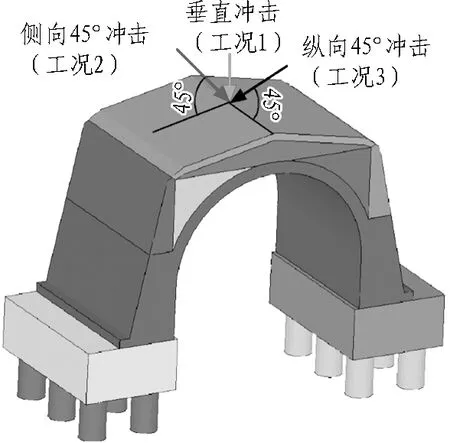
(b) 模型三维视图
根据文献[5]设计情况,所建模型分为3部分: 1)上部结构,包括左、右墙和拱部; 2)下部结构,包括承台和桩基; 3)缓冲层,在拱部与耳墙间采用C20混凝土填充,拱部上部为夯填土石,最上面为黏土隔水层。模型中各部分尺寸见图1,结构纵向取11 m,承台下部纵向有3排桩,纵向桩间距(中心线之间)为4 m。桩出露土层部位为3 m,桩底设为全约束。
在数值模拟中,模型中钢筋混凝土结构及缓冲层中混凝土填充采用弹性材料单元,夯填土石及黏土隔水层采用DP材料模拟,为研究落石冲击荷载,在DP材料与弹性材料之间设置接触面,而上部、下部各部件之间采用固结,落石采用球形刚体单元。计算所需材料物理力学参数选取见表1,其中钢筋混凝土参数由其配筋率等效换算得到[13]。
为了解落石冲击下拱形护桥明洞结构力学响应的一般规律,本次选取中等尺寸规模落石但又要具有一定冲击能量,以使结构有全面响应。根据以往我国铁路落石事件的调查统计数据[14],本次落石选取质量为2 000 kg(重度取25.7 kN/m3)的球体,其半径为0.5 m、体积为0.77 m3。落石底部与黏土隔水层顶点垂直高度为50 m,分别以垂直、沿结构纵向(相当于落石从隧道上方仰坡滚落)45°和侧向(落石从线路两侧边坡下落)45°角度冲击结构顶部黏土隔水层顶点处,冲击点位于结构纵向中部断面,如图2(b)所示。
为便于叙述,后续说明中,将垂直下落冲击称为工况1,沿结构侧向45°冲击为工况2,纵向45°冲击为工况3。

表1 材料物理力学参数
2 结果及分析
从落石在冲击过程中的运动轨迹入手,分别分析结构最大剪应力(max shear stress)、应变、应变率及位移等荷载效应,为明确落石冲击荷载,本次分析落石与缓冲层间的相互作用力、由缓冲层传递到拱顶的冲击荷载等。
2.1 落石运动轨迹
在冲击过程中,落石运动轨迹也可以用侵彻缓冲层深度来描述。落石侵彻缓冲层深度涉及到落石与回填土等材料相互作用中的能量转化,一般,落石侵入回填土深度越大,传递到结构的荷载或冲击能量越小,这样是有利于结构受力的,但也不能侵入太深,否则会完全穿透缓冲层,直接与结构作用[6]。因此,研究落石侵彻深度有助于设计者了解结构受力过程和合理确定回填土厚度。
3种不同冲击角度落石运动轨迹如图3所示,为便于描述,将落石与黏土隔水层顶部刚接触时所处位置设为参考点,后续落石位移都是相对于此参考点的相对位移,为便于理解,每个工况对应的落石从开始碰撞到完成的不同时刻数值模拟结果也示于图3中。


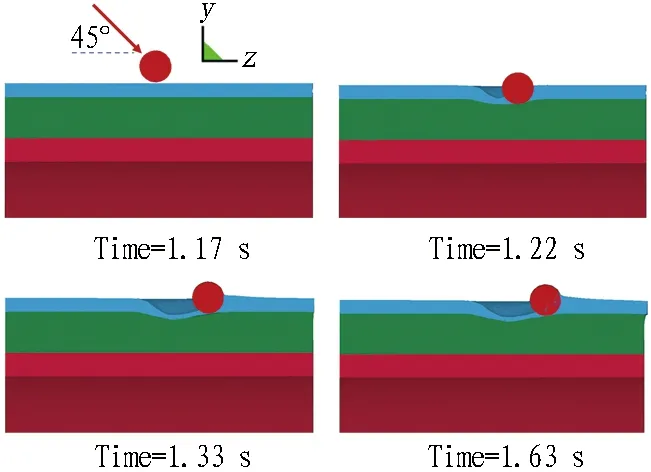
图3(a)为工况1,垂直下落的落石从开始与黏土层接触(Time=1.175 s)到侵彻入缓冲层最大深度0.90 m(Time=1.24 s),共用时0.065 s,随后发生反弹,到达最高点(Time=1.7 s,超出参考点0.08 m)后,在重力下重新下落,本次计算共用了2 s,没有分析落石二次下落冲击。
图3(b)为工况2,即落石从侧向以45°冲击,在Time=1.17 s时与黏土层接触,沿隔水层坡面向下和水平向(x方向)运动,冲击黏土隔水层形成一个斜向下的最大深度约为0.5 m、长约2.2 m的冲槽,在Time=1.39 s时反弹飞离土层,冲击过程历时约0.22 s。
图3(c)为工况3,即落石沿结构纵向以45°冲击,在Time=1.17 s时与黏土层接触,沿隔水层坡面向下和水平纵向(z方向)运动,冲击黏土隔水层形成一个斜向下的最大深度为0.74 m、长约2.0 m的冲槽,在Time=1.33 s时达到最大深度,然后落石发生少许反弹后并停留在冲击位置处,回填土也恢复一部分变形,在Time=1.446 s时停止运动,冲击历时约0.28 s。
通过以上分析可知: 落石与缓冲层相互作用时间大小关系是: 工况1<工况2<工况3(工况1只考虑首次冲击);侵彻缓冲层深度大小关系是: 工况2<工况3<工况1,在本次计算范围,3种工况下落石均未穿透缓冲层。
2.2 结构应力
本次以最大剪应力为代表进行结构内力响应分析。通过搜索功能,找出结构各部位不同时刻最大剪应力的部位,以此确定冲击下结构最不利部位。
通过对计算结果的分析,发现3种工况下结构应力最大部位基本相同,且各工况在落石冲击前自重作用下、冲击过程中及冲击完成稳定后3个阶段中,应力最大部位也基本不变。工况1中3个阶段的最大剪应力云图如图4所示(工况2和工况3的情况类似,不再列出)。

(a) 自重平衡后(t=1 s) (b) 落石冲击时(t=1.23 s)(c) 落石冲击稳定后(t=1.7 s)
图4工况1结构最大剪应力云图
Fig. 4 Nephograms of maximum shear stress of structure in case 1
由图4可知: 在落石冲击前、落石冲击时及落石冲击稳定后,结构最大剪应力集中部位基本保持不变,这些受力不利部位包括拱顶、拱脚、边墙墙脚外侧、外侧桩基顶部与承台连接处内侧和与地面连接处的外侧。因此在数值计算过程中需要对这些受力不利部位的力学响应进行监测分析,其监测点布置如图5所示。
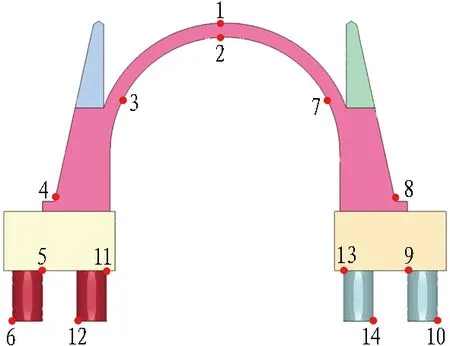
图5 监测点布置
按结构部位,以拱顶为例,对3种工况同一测点处的应力时程特征进行对比分析。拱顶处外侧、内侧最大剪应力时程响应如图6所示。

(a) 拱顶外侧(1号测点)

(b) 拱顶内侧(2号测点)
由图6(a)可知: 落石由不同方向进行冲击,结构的最大剪应力变化规律基本一致。在自重作用下拱顶外测(测点1)的最大剪应力为1.34 MPa,结构受到落石冲击后,结构的最大剪应力迅速增大,达到最大值后再迅速减小,在一系列轻微震荡后趋于稳定。工况1时,测点1的最大剪应力最大峰值为3.22 MPa,比未冲击时增大3.22-1.34=1.88 MPa,变化率为1.88/1.34=140.3%,在本文此后的叙述中,相对于冲击前的变化幅度称为冲击附加值,其与冲击前的比值称为变化率;工况2时,测点1处的最大剪应力峰值最小,其最大值为1.95 MPa,附加值为0.61 MPa,变化率为45.5%;工况3时,测点1的最大值为2.33 MPa,附加值为0.99 MPa,变化率为73.9%。
由图6(b)可知: 未冲击前,拱顶内侧(测点2)的最大剪应力为0.7 MPa。工况1时,测点2的最大剪应力最大峰值为2.42 MPa,附加值为1.72 MPa,变化率为245.7%;工况2时,最大峰值为1.19 MPa,附加值为0.49 MPa,变化率为70%;工况3时,最大峰值为1.49 MPa,附加值为0.79 MPa,变化率为112.9%。
按上述分析方法,对结构各部位不同测点处的最大剪应力响应总结如表2所示。
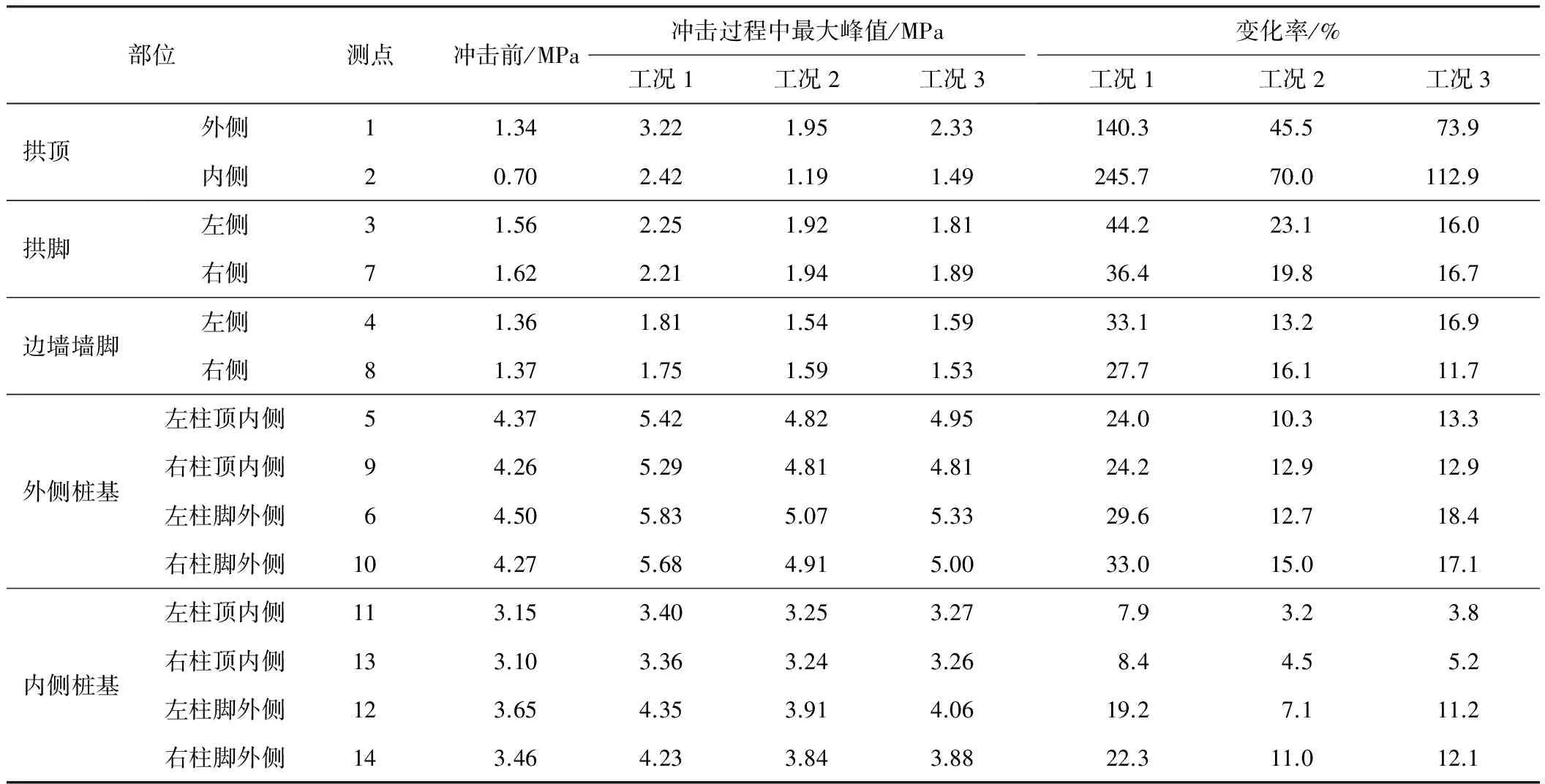
表2 结构最大剪应力响应
注: 变化率=(冲击过程中最大峰值-冲击前剪应力)/冲击前剪应力,下同。
根据表2数据,对不同受力阶段结构应力响应特征分析如下:
1)在落石冲击前,即在回填土及结构自重作用下,护桥明洞受力较大部位是下部桩基的柱顶内侧(测点5、9、11、13)和柱脚外侧部位(测点6、10、12、14),且外侧桩基受力要大于内侧桩基;同一立柱的柱脚受力大于柱顶,如图5中左侧立柱测点6最大剪应力为4.5 MPa,而测点5为4.37 MPa。
2)在落石冲击过程中,结构不利受力部位仍与自重时一致,下部桩基的最大剪应力峰值大于上部结构构件;不同工况下各部位达到的最大应力峰值关系是工况1最大,即落石垂直冲击时结构应力响应最大;而拱脚部位(测点3和7)及右侧边墙墙脚(测点8)则是工况2>工况3,除此外,均是工况3>工况2,即沿结构纵向45°大于侧向45°冲击;工况2时,上部结构右侧应力要稍大于相应左侧部位,如测点8大于测点4,测点7大于测点3,而下部结构则基本相等。
3)从落石冲击时与冲击前结构应力的变化率看,3种工况下,都是拱顶部位变化最大,且拱顶内侧(测点2)比外侧(测点1)更显著,如工况1时,测点2最大应力峰值为冲击前的2.4倍多;3种工况中工况1引起的结构应力变化幅度最大,与工况3相比,工况2对拱脚部位(测点3和7)及右侧边墙墙脚(测点8)引起的应力变化率要大于工况3,其他测点则均小于工况3。
2.3 结构应变
对落石冲击前和冲击时不同工况下结构各部位的最大主应变(拉应变)和最小主应变(压应变)进行分析,其中,拱顶外侧部位(测点1)的最大、最小主应变时程响应如图7所示。
由图7可知: 落石冲击前,在自重作用下拱顶部位(测点1)的最大主应变(拉应变)为1.53×10-5,最小主应变(压应变)为7.0×10-5,结构受到落石冲击后,结构的应变迅速增大,达到最大值(绝对值)再迅速减小,在一系列震荡后趋于稳定。工况1时,测点1的最大主应变为2.54×10-5,附加值为1.01×10-5,变化率为66%,最小主应变为17×10-5,附加值为10×10-5,变化率为142.9%;工况2时,测点1的最大主应变和最小主应变最大值(绝对值)分别为2.14×10-5和1.0×10-5,其附加值分别为0.61×10-5和3.0×10-5,变化率分别为39.9%和42.9%;工况3时,测点1的最大主应变为2.72×10-5,附加值为1.19×10-5,最小主应变为1.2×10-5,附加值为5×10-5,变化率分别为77.8%和71.4%。
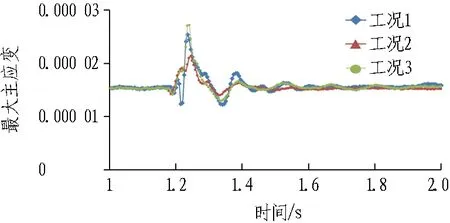
(a) 最大主应变

(b) 最小主应变
按上述分析方法,得到不同工况下结构应变响应结果,见表3和表4。
根据表3和表4数据,对不同工况落石冲击下,结构各部位的应变响应特征分析如下:
1)落石冲击前,即在回填土和自重作用下,结构的最大、最小主应变分布规律与结构应力特征规律一致,应变最大的部位均为结构下部的外侧柱脚外侧(测点6、10),其次是内侧柱脚外侧(测点12、14)。
2)冲击过程中,结构达到的最大应变峰值大小特征与冲击前分布特征一致,仍是外侧柱脚外侧(测点6、10)的应变峰值最大,其次是内侧柱脚外侧(测点12、14);不同工况下各部位达到的最大、最小主应变峰值(绝对值)关系是工况1最大,即落石竖向冲击时结构应力响应最大;与最大剪应力稍有不同的是,对于应变响应,均是工况3>工况2,即沿结构纵向45°大于侧向45°冲击;工况2时,上部结构右侧应变大于相应左侧部位,如测点8大于测点4,测点7大于测点3,而下部结构左右差别则不明显。
3)从结构应变的变化幅度看,3种工况下,都是拱顶部位变化最大,且拱顶内侧(测点2)比外侧(测点1)更显著;3种工况中工况1引起的结构应变变化率最大,工况3的应变变化率大于工况2;工况2时,结构右侧应变变化率要大于相应左侧部位。
4)在本次研究范围内,在各工况落石冲击下,结构的最大拉应变(最大主应变)为工况1时拱顶内侧的测点2处,为7.63×10-5,小于《混凝土结构设计规范》[15]中的极限值1×10-4,结构的最大压应变(最小主应变)为工况1时外侧桩基左柱脚外侧测点6处,为3.35×10-4,小于《混凝土结构设计规范》[15]中的极限值0.003 3或0.002 0。

表3 最大主应变(拉)最大峰值
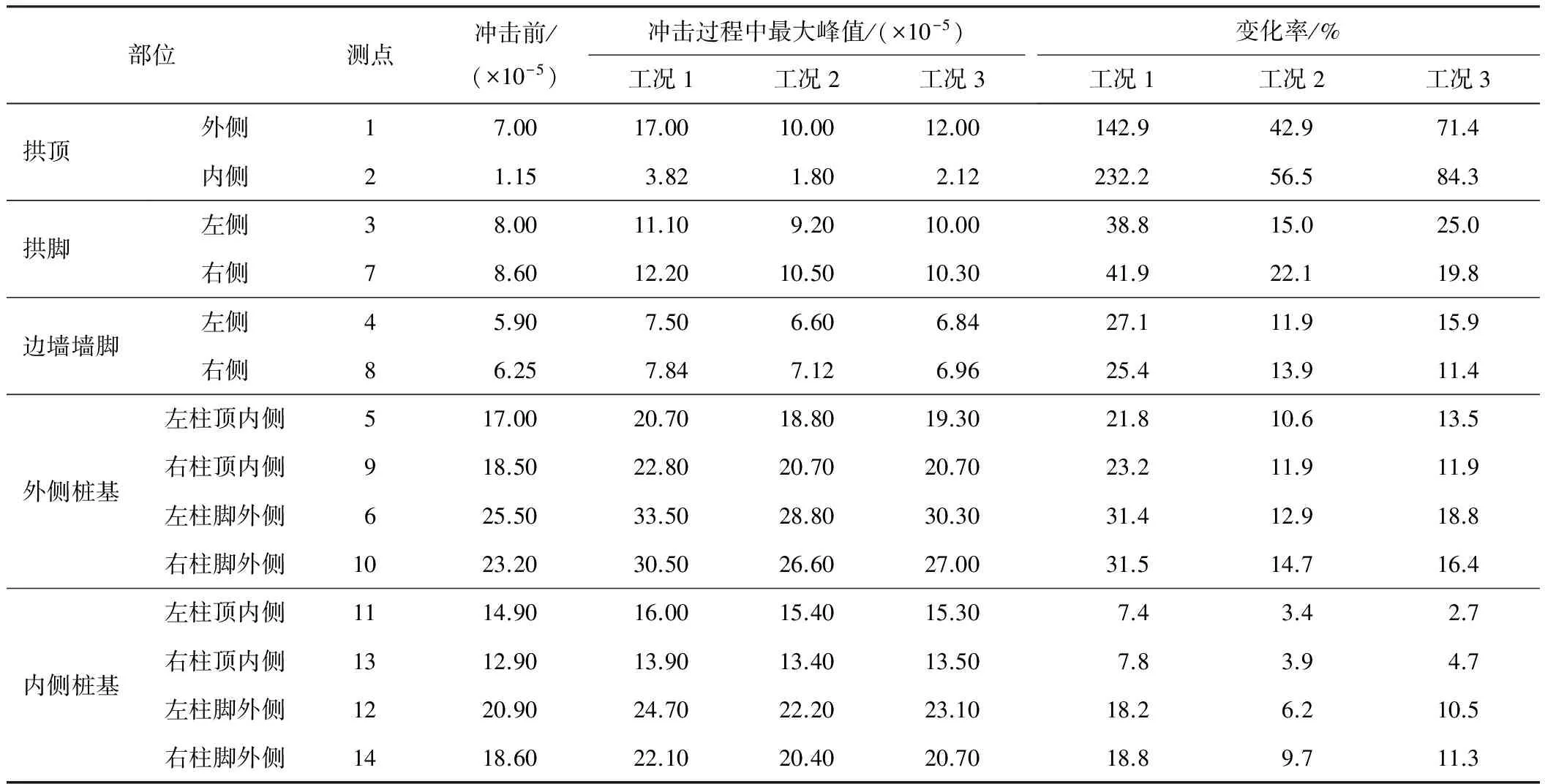
表4 最小主应变(压)最大峰值
2.4 结构应变率
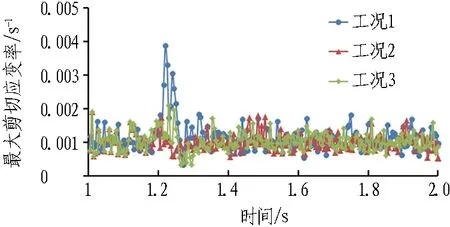
由于混凝土为率相关材料,有必要了解落石冲击下结构的应变率响应,本次以结构最大剪应变率为代表,提取不同工况下结构各部位最大剪应变率,以拱顶部位测点1和测点2为例,其不同工况下最大剪应率如图8所示。
(a) 1号测点

(b) 2号测点
由图8(a)可知: 测点1的最大剪应变率峰值在工况1时最大,为3.9×10-3s-1;工况2时最小,为1.72×10-3s-1;工况3时为2.1×10-3s-1。
由图8(b)可知: 测点2的最大剪应变率峰值在工况1时最大,为2.66×10-3s-1;工况2时最小,为0.95×10-3s-1;工况3时为1.0×10-3s-1。
按上述分析方法,不同工况下结构各部位最大剪应变率最大峰值如表5所示。
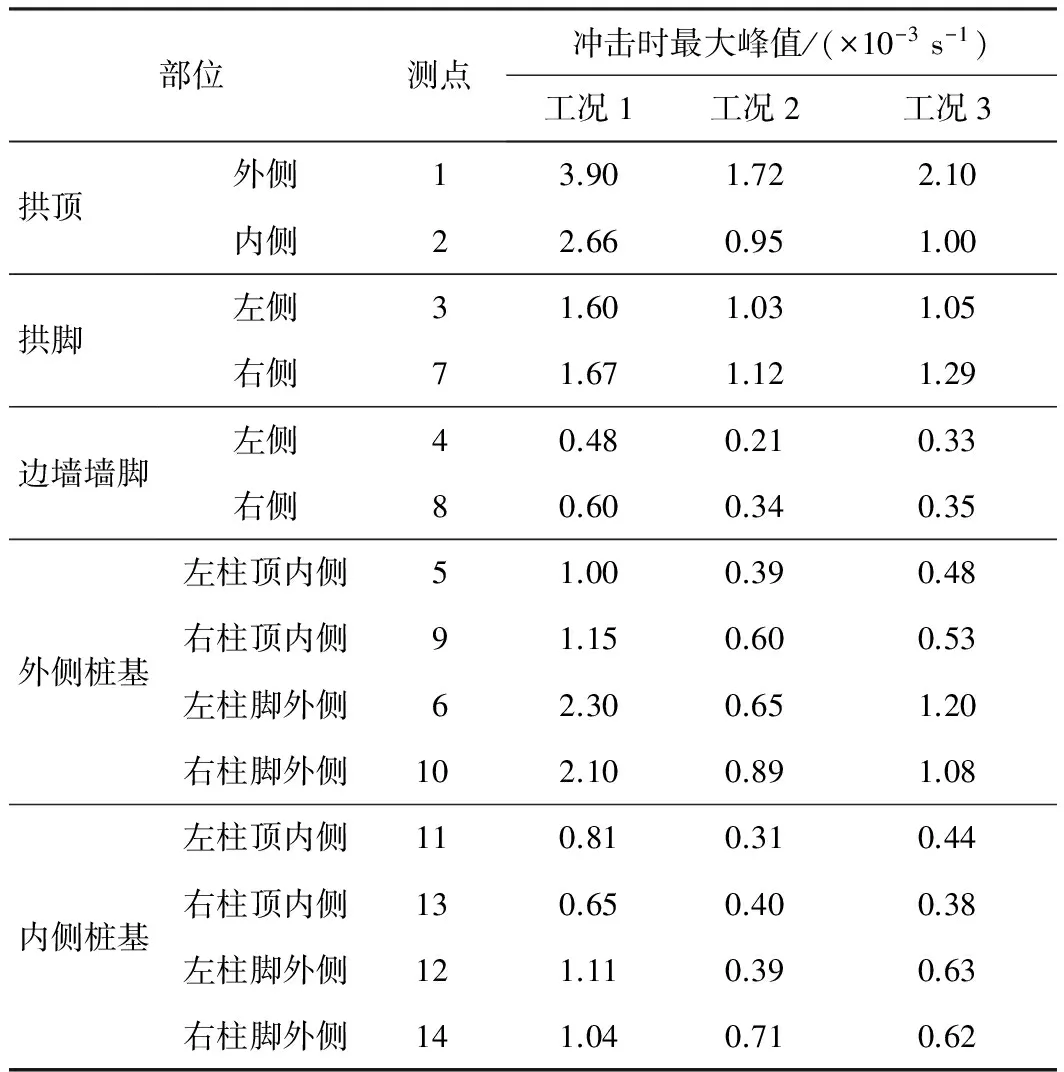
表5 结构最大剪应变率
由表5可知: 不同工况落石冲击结构同一部位引起的应变率最大峰值的关系总体为工况1>工况3>工况2,说明垂直冲击引起的结构响应大于斜向冲击;同一工况时,拱顶部位尤其是拱顶外侧(测点1)应变率峰值最大,同一部位外侧要大于内侧,如测点1大于测点2,测点5大于测点11;工况2时,即侧向45°冲击时,右侧尤其是下部桩基部位响应要明显大于左侧;在本次工况范围内,以上各应变率为10-3~10-4s-1,并未达到通常所说的1~10 s-1冲击荷载下结构的应变率[16]。
2.5 结构位移
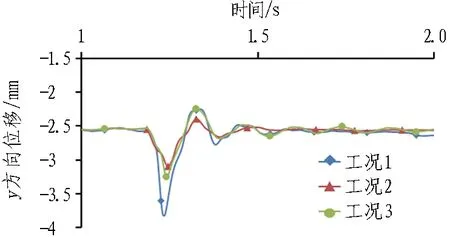
不同工况落石冲击下结构位移或变形响应,以拱顶外侧(测点1)部位的竖向和水平位移为例,其位移时程响应如图9所示。
将落石冲击前、冲击过程中各工况下结构位移变化特征示于表6中,由于下部结构位移相对于上部结构不明显,故表6中只列出护桥明洞的上部结构部分测点位移结果。
(a) 1号测点竖向位移 (b) 1号测点水平位移
图9 拱顶部位位移时程响应
由图9和表6可知:
1)落石冲击前,在回填土及自重作用下,结构拱顶部位竖向位移最大,测点1为2.53 mm,拱脚和边墙则不到1 mm,而拱脚和边墙脚处的水平位移为0.94 mm。
2)在落石冲击中,拱顶竖向位移峰值最大,工况1时测点1为3.82 mm,其次为工况3的3.25 mm和工况2的3.10 mm。
3)在落石冲击中,拱脚处竖向位移在工况2时响应最大,其次是工况1,工况3最小,说明侧向冲击对拱脚部位影响较显著。
4)工况2时,拱顶水平位移变化最大,变化率达到500%,但水平位移峰值并不大,为0.23和0.27 mm,除拱顶外,拱脚和边墙的水平位移响应仍是工况1最大,工况2和工况3相差不多。
2.6 落石冲击力与冲击荷载
落石在冲击过程中,先与结构缓冲层表面接触再发生碰撞,在未完全穿透缓冲层前,落石的冲击是通过缓冲层传递到结构表面,落石与缓冲层之间的相互作用可以称为落石冲击力,而通过缓冲层传递到结构表面的力,在本文中则称为落石冲击荷载,其与落石冲击力含义并不相同。另外,考虑到结构荷载效应主要是受垂直冲击荷载的影响,故本次不同冲击方向只分析垂直落石冲击力与冲击荷载。
2.6.1 落石冲击力
为研究落石与缓冲层之间的相互作用力,即落石冲击力,需先知道落石的冲击加速度,提取不同工况下落石垂直加速度响应如图10所示。
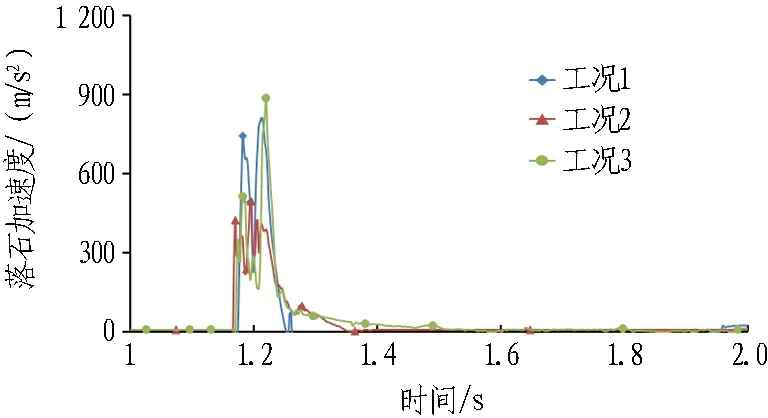
图10 落石加速度时程响应
由图10可知: 工况1时,落石最大加速度峰值为808 m/s2,工况2时为500 m/s2,工况3时为889 m/s2。
根据牛顿第二定律,落石冲击中,其受到的冲击力F=ma,根据上述得到的垂直落石加速度最大峰值,得到工况1时,落石垂直最大冲击力峰值为1 616 kN,工况2时为1 000 kN,工况3时为1 778 kN。
2.6.2 落石冲击荷载
在回填土与混凝土填充之间设置3个接触面,分别测取由缓冲层传递下来的落石冲击荷载,3个接触面分别为左右侧的S1和S2,以及中部S3,S1与S2的宽度均为6 m,S3的宽度为2.4 m,如图11所示。

图11 落石冲击荷载接触面设置(单位: m)
提取3个接触面的竖向落石冲击荷载时程响应,如图12所示。


(a) 左侧S1 (b) 右侧S2 (c) 中部S3
图12落石冲击荷载时程曲线
Fig. 12 Time-history curves of rock-fall impaction loads
由图12(a)可知: 冲击前,在缓冲层自重作用下,左侧S1,即回填土与结构左侧的C20填充间的接触力为1 290 kN,在工况1的落石冲击下,S1的接触力即本文所指的落石冲击荷载,其最大峰值为1 690 kN,比初始值增加400 kN,工况2时最大峰值为1 420 kN,附加值为130 kN,工况3时最大峰值为1 570 kN,附加值为280 kN。
根据上述分析方法,对3个接触面的落石冲击荷载响应特征以及落石冲击力示于表7。

表7 落石冲击力及冲击荷载
注: 附加值=冲击时最大峰值-冲击前受力。
由表7数据分析如下:
1)对于左侧接触面S1和中部S3,不同工况落石冲击下接触力变化率的关系均为工况1>工况3>工况2,即垂直冲击下落石冲击荷载最大,沿结构纵向45°冲击次之,侧向45°冲击时最小;而对于右侧接触面S2,接触力变化率关系则为工况2>工况1>工况3,即侧向45°冲击时对右侧接触面S2的冲击荷载最大。
2)工况1即落石垂直冲击结构上方时,中部S3受到的落石冲击荷载峰值明显大于左右两侧,比冲击前增大了230%,说明垂直冲击时,由缓冲层传递到结构顶部的落石冲击荷载主要集中在中部一定范围,S3的宽度为结构顶部总宽度的16.7%(即2.4/(2.4+6+6)),但落石冲击荷载峰值占了整个范围的44.9%(即2 798/(2 798+1 740+1 690))。
3)冲击过程中,落石与缓冲层间的相互作用力,即本文所指的落石冲击力,与由缓冲层传递到结构表面的冲击荷载是2个不同概念,落石冲击荷载与落石冲击力大小有关,同时也与缓冲层性质有关,单独研究缓冲层表面的落石冲击力对结构设计并无太大意义,因为真正作用在结构上的是由缓冲层传递到结构表面的落石冲击荷载。
4)为验证数值计算的有效性,可对比由数值计算得到的混凝土填充面上的接触力与理论计算得到的上覆回填缓冲层的自重。
①理论计算: 黏土隔水层的自重=断面积×纵向长度×容重=7.25×11×15=1 196.25 kN,同理,回填土(夯填土石)自重=12.343×11×18=2 443.9 kN,二者合计3 640.1 kN;
②数值计算: 由表7可知,冲击前,S1、S2、S3 3个接触面(见图11)的接触荷载和为1 290+1 290+849=3 429 kN。
通过以上对比可知,由数值计算得到的回填层自重比理论计算的稍小,原因如下: ①数值计算中3个接触面面积并未包括耳墙顶部部分;②有限元划分网格时,由于结构形状不规则,划分网格后实际面积或体积要小于实际模型图。
综上,缓冲层自重的数值计算结果与理论计算结果相符。
3 结论与讨论
3.1 结论
本次选取半径为0.5 m、体积为0.77 m3、质量为2 000 kg 的中等尺寸规模落石,从50 m高度以垂直、侧向45°和纵向45° 3个不同方向冲击结构缓冲层顶部中心,研究落石冲击下拱形护桥明洞结构力学响应特征,得出如下结论:
1)根据落石冲击缓冲层后的运动路径看,垂直冲击时落石侵彻缓冲层深度相对其他2种斜向冲击是最大的,冲击作用时间也最短,侧向45°时落石与缓冲层表层作用后会飞出明洞范围,而沿纵向45°冲击时落石在缓冲层中运动路径长度最长,作用时间也最长,落石最终留在缓冲层内部,3种工况下落石的最大竖向侵彻深度为竖向冲击时的0.9 m,小于缓冲层设计厚度2 m,在本次研究范围内,落石冲击引起的结构应变最大峰值均小于混凝土材料的极限值,说明结构可以承受本次计算的落石冲击作用。
2)从落石冲击时与冲击前结构应力、应变及位移的最大峰值及变化率看,护桥明洞结构在落石冲击过程中的受力不利部位,与冲击前结构在缓冲层及结构自重作用下的受力不利部位相同,这些受力不利部位包括拱顶、拱脚、边墙墙脚外侧、桩基顶部与承台连接处、桩基与地面连接处等,且外侧桩基受力要大于内侧桩基;同一立柱的柱脚外侧受力大于柱顶内侧。
3)落石竖向冲击结构上方时,由缓冲层传递到结构顶部的落石冲击荷载主要集中在中部一定范围。
4)在本次计算工况下,相同落石且相同冲击能量时,垂直冲击引起的结构荷载效应最大,因此在类似工程设计时,可以把垂直冲击作为不利工况进行结构承载力的检算,其中拱顶部位、下部结构桩基与承台和地面的连接部位,尤其是外侧立柱柱脚外侧和柱顶内侧部位是受力最不利部位或是控制截面,设计中应予以加强。
3.2 讨论
本次是采用数值模拟方法进行研究,有如下问题需要讨论或需要开展进一步的研究。
1)本次数值模拟的落石冲击能量约为1 000 kJ,在此工况下,所得结构内力响应均没有超出相应静力学条件下的规范值,由此作者认为,结构可以承受1 000 kJ的落石冲击能量。曾廉在文献[14]中指出:“例如宝成线K180+700处的明洞,1970年4月25日从洞顶以上40 m处坠落到洞顶的一块1 m3的岩块,对该处厚3 m的回填土的明洞无影响,又如该线K246+659处的明洞,1966年7月3日从洞顶以上35 m处坠落到洞顶的一块1.2 m3的岩块,对该处3 m厚的回填土明洞也无影响”。如文中,如果岩块的重度为 20~25 kN/m3,则冲击能量接近1 000 kJ。
2)本次主要分析了结构整体受力情况,只给出了落石冲击下结构受力不利部位,从定性上建议了设计应注意的关键部位。如何将数值计算中得到的落石冲击荷载提炼出一个实用表达式,作为偶然荷载与恒载进行组合、提出类似于地下结构抗震检算的静力法以便于结构设计,将是进一步研究的方向。
[1] 王玉锁, 杨国柱. 隧道洞口段危岩落石风险评估[J]. 现代隧道技术, 2010, 47(6): 33.
WANG Yusuo, YANG Guozhu. Rockfall risk assessment for a tunnel portal section[J]. Modern Tunnelling Technology, 2010, 47(6): 33.
[2] 王玉锁. 高速铁路隧道洞口段危岩落石运动轨迹及冲击特性研究[J]. 学术动态, 2011(2): 16.
WANG Yusuo. Study of motion trail and impact characteristics of unstable rock and rockfall on the tunnel portal section of high-speed railway[J]. Academic Trends, 2011(2): 16.
[3] 王全才, 王兰生, 李宗有, 等. 都汶路恢复重建中的主要地震次生山地灾害与明洞工程[J]. 山地学报, 2011, 29(3): 356.
WANG Quancai, WANG Lansheng, LI Zongyou, et al. Open tunnel engineering and secondary disasters of earthquake in the post-earthquake reconstruction projects along Duwen Road[J]. Journal of Mountain Science, 2011, 29(3): 356.
[4] 王玉锁, 周良, 李正辉, 等. 落石冲击下单压式拱形明洞的力学响应[J]. 西南交通大学学报, 2017, 52(3): 505.
WANG Yusuo, ZHOU Liang, LI Zhenghui, et al. Mechanical responses of single-pressure arch-shaped open tunnel structure under rockfall impaction[J]. Journal of Southwest Jiaotong University, 2017, 52(3): 505.
[5] 张慧玲, 唐辉, 唐元峰, 等. 高速铁路护桥棚洞结构. 201120212046.1[P]. 2012-05-23.
ZHANG Huiling, TANG Hui, TANG Yuanfeng, et al. High-speed railway shed tunnel for bridge protection. 201120212046.1[P]. 2012-05-23.
[6] 何思明, 沈均, 吴永. 滚石冲击荷载下棚洞结构动力响应[J]. 岩土力学, 2011, 32(3): 781.
HE Siming, SHEN Jun, WU Yong. Rock shed dynamic response under impact of rock-fall[J]. Rock and Soil Mechanics, 2011, 32(3): 781.
[7] 汪敏, 石少卿, 阳友奎. 柔性棚洞在落石冲击作用下的数值分析[J]. 工程力学, 2014, 31(5): 151.
WANG Min, SHI Shaoqing, YANG Youkui. Numerical simulation of a flexible rock shed under the impact of a rockfall[J]. Engineering Mechanics, 2014, 31(5): 151.
[8] 刘成清, 陈驰. 落石冲击作用下钢筋混凝土棚洞结构的动力系数研究[J]. 施工技术, 2014, 43(17): 46.
LIU Chengqing, CHEN Chi. Study of the dynamic coefficient of rock shed under rock-fall impact [J]. Construction Technology, 2014, 43(17): 46.
[9] 王琦, 王玉锁, 耿萍. 橡胶缓冲垫层保护下棚洞结构落石冲击力学响应研究[J]. 铁道建筑, 2017(2): 64.
WANG Qi, WANG Yusuo, GENG Ping. Research on mechanical response of tunnel shed with protective rubber cushion subjected to impact of rockfall[J]. Railway Engineering, 2017(2): 64.
[10] WANG Yusuo, ZHANG Keyue, TANG Jianhui, et al. Model test research of the influences of rock-fall impaction on accelerations of the cut-and-cover tunnel structure[J]. Applied Mechanics and Materials, 2012, 117: 206.
[11] WANG Yusuo, TANG Jianhui, YAN Tao, et al. Model test investigation of rock-fall impaction to cut-and-cover tunnel arch structure[J]. Applied Mechanics and Materials, 2011, 90: 2492.
[12] 王爽, 周晓军, 罗福君, 等. 拱形棚洞受落石冲击的模型试验研究[J]. 振动与冲击, 2017, 36(12): 215.
WANG Shuang, ZHOU Xiaojun, LUO Fujun, et al. An experimental study of the performance of an arch-shaped shed tunnel due to the impact of rockfall[J]. Journal of Vibration and Shock, 2017, 36(12): 215.
[13] 程选生, 杜永峰. 正交各向异性钢筋混凝土板结构弹性常数的确定[J]. 四川建筑科学研究, 2006, 32(5): 30.
CHENG Xuansheng, DU Yongfeng. Confirm of elasticity cofficient about or thotropic plates of reinforced concrete[J]. Sichuan Building Science, 2006, 32(5): 30.
[14] 曾廉. 明洞顶设计荷载的研究[J]. 铁路标准设计通讯, 1974(7): 3.
ZENG Lian. Research on designing load on top of open cut tunnel[J]. Railway Standard Design Communication, 1974(7): 3.
[15] 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010.
Code for design of concrete structures:GB 50010—2010[S]. Beijing: China Architecture & Building Press, 2010.
[16] 余同希, 邱信明. 冲击动力学[M]. 北京: 清华大学出版社, 2011.
YU Tongxi, QIU Xinming. Impact dynamics[M]. Beijing: Tsinghua University Press, 2011.
