罐装水泥船甲板结构改进与舯剖面优化设计

覃达斌，黄琼念

（广西交通职业技术学院，广西 南宁 530023）

0 引言

罐装水泥船是近年来在广西悄然兴起的新型船舶，基于对生态环境与生命健康的保护，其相对于敞口散装水泥船具有巨大的环保优势。散装水泥水路运输目前仍然广泛使用大开口干货船运输，若将其升级为罐装封闭式运输，将使装卸运输环境及装卸效率得到明显改善。水泥罐装封闭运输在节约资源、保护环境、生命健康、装卸效率等方面具有显著优势，推广罐装水泥运输船对于广西具有重大的现实意义。

本文基于一艘罐装水泥运输船，对两个问题进行深入研究：

（1）利用有限元直接计算法，建立船舶模型，校核其结构强度是否满足规范要求，若不满足，则再提出解决方案。用模型模拟整改后的船舶结构，验证解决方案的合理性，并选出最优方案。

（2）利用蚁群算法，结合经验设计及规范计算，优化货舱结构尺寸，对应力很小的结构进行减轻，达到降低结构重量以及运输能耗的作用。

经有限元直接计算，目标船货舱区域甲板局部应力较大，发生局部损坏的可能性较高，应对此区域结构进行重新设计，以降低应力水平，保证航行安全；同时，经蚁群算法，目标船舶的结构设计较为保守，有进一步优化的必要性。

1 技术方法与原理

船体结构设计目前包含确定性设计法和结构可靠性分析法。

基于目标船的实际运营情况，本文采用有限元直接分析法进行船体结构的调整与优化设计。根据实际运营情况及直接计算的结果，确定船体甲板结构的高应力区域，通过调整结构布置，优化局部结构受力状态。在显著降低全船高应力区域的应力水平条件下，应用蚁群算法对船体主要的支撑板架结构进行分析，优化结构的布置与尺寸，实现结构减重的目标。目标船优化分析采用的计算软件为Patran与Nastran，优化程序采用Python脚本语言、PCL语言编写。

2 甲板结构形式的调整

本次分析的罐装水泥船主尺寸为：

总长 Loa：73.43m；计算船长：71.80m；设计水线长Lwl：72.95m；型宽B：15.55m；型深D：6.00m；设计吃水：5.00m，甲板开口宽12.50m。目标船的有限元模型如图1所示。

图1 全船有限元模型图

目标船为双机、双浆的双壳尾机型灌装水泥运输船；其货舱区域采用纵骨架式，其余区域采用横骨架式。货舱区域布置3排6个水泥罐。按照全船有限元校验要求，将船体结构、罐体及罐体鞍座进行整体建模，以校核复杂工况下各部分的相互影响。为了消除模型的刚体位移，在计算分析中采用惯性释放处理边界条件［4］。根据目标船的航区及装载情况，共计算A级航区条件下的满载出港、空载到港2种装载模式，结合波浪中拱、中垂2种波浪条件，计算分析4种计算工况，如表1所示。

表1 计算工况列表

2.1 结构问题

模拟计算表明，目标船罐体边甲板与舱口围板连接处的局部结构（图1中的放大区域）发生破坏。经有限元直接计算结果分析，发现此处结构的应力值较高，超过规范限值。直接计算的数值结果（如下页表2所示）显示LCA、LCB、LCC工况下的应力峰值均大幅超过限值。以LCA工况为例，其甲板应力云图如图2、图3所示。

表2 四种工况下甲板应力峰值表（N／mm2）

2.2 原因分析

图2、图3中罐体间甲板结构的主要作用是提供人员通道、管系支撑与罐体固定限位。其结构形式为横骨架式，无纵骨，非主要支撑结构，即在结构功能上并不承担或传递船体的内外载荷。由于其与主甲板、舱口围板及罐体刚性连接，在船长方向保持结构连续但并无纵向骨材，使其直接承担或传递船体纵向载荷，导致局部结构应力水平太高而发生结构破坏。

图2 满载中拱工况甲板船长方向应力云图（方框表示高应力区域）

图3 满载中拱工况甲板相当应力云图（方框表示高应力区域）

2.3 解决方法

可从阻断载荷传递及增强结构强度两种思路调整此处结构：思路1是去除高应力区域与整体结构的刚性连接以阻断载荷传递；思路2是在此区域布置纵向骨材以增强结构强度。对应上述的两种思路，本文采用两种方法对结构进行调整，以期达到降低局部应力水平的目标，并通过有限元直接计算进行对比分析。

方法1：在全船有限元模型中，删除高应力区域与罐体及舱口围板连接的网格单元（图1中的方框部分），使原来的纵向连续结构成为间断的三部分：仍与罐体、甲板间相连的部分不再承担或传递船体（纵向）载荷，仅提供固定限位作用；由于替代结构不与船体刚性连接，因此不在模型中表达。调整后的甲板局部结构模型如图4所示。

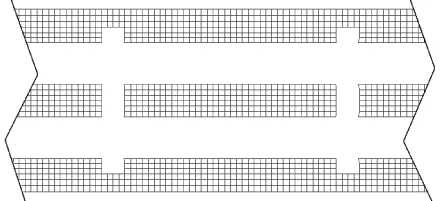
图4 去除高应力区域刚性连接处的网格单元图

方法2：在高应力区域部分添加纵骨，纵向范围分别向首尾延伸3个肋位，间距与内底纵骨间距保持一致，即400～500mm。调整后的甲板局部结构模型如图5所示。骨材的截面类型与其他甲板纵骨保持一致，即采用L100mm×63mm×8mm。

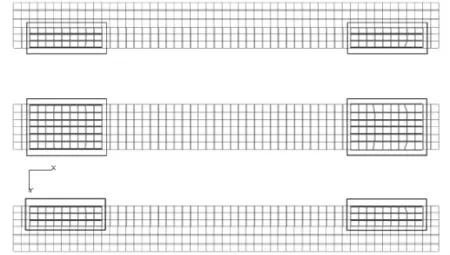
图5 高应力区域增加纵向骨材（方框中显示的纵向构件）网格单元图

2.4 计算结果及分析

经对比，上述两种调整方法对主船体结构（除甲板外的构件）、主船体与罐体鞍座连接处的影响可以忽略。

两种方法的计算结果如表3、表4所示。通过与原始计算结果对比分析可知：两种方法均显著降低了连接处的应力水平，且方法1应力值降幅较大，按照方法1调整后的甲板结构应力水平达到了规范要求，且显著低于规范限值；按照方法2调整后的应力水平仍然较高，且处于规范限值左右。因此，经方法1调整后的局部结构应力水平改善明显，且满足规范要求，其应力分布状态更优。

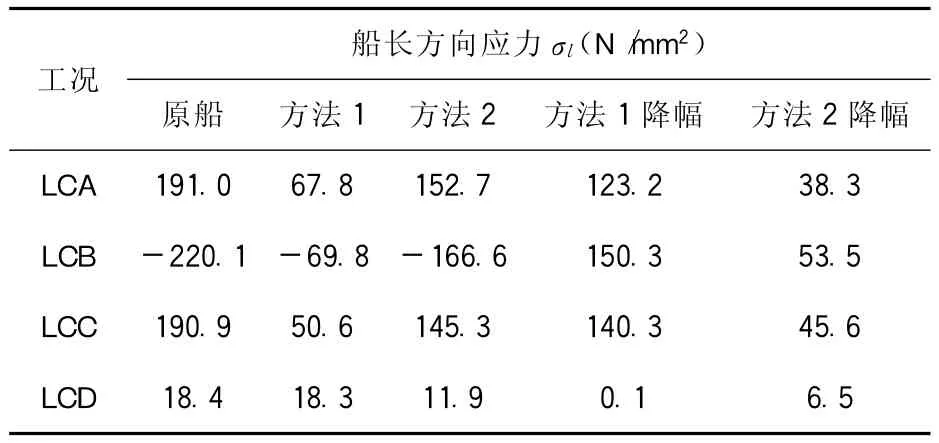
表3 甲板结构船长方向应力计算结果对比表

表4 甲板结构von Mises应力计算结果对比表

综合计算对比结果，建议在实际改装中采用方法1，这样既能达到降低局部应力的目的，也能满足初始设计的结构功能。

3 船体结构形式的优化设计

通过有限元直接计算的结果进行统计分析可知：92%的板结构（按单元数统计）单元的屈服应力处于20～60 MPa之间，94%的梁结构（按单元数统计）单元的轴向应力处于10～45 MPa之间。因此，目标船主船体结构在运营工况下的整体应力状态处于较低水平，结构利用率不高，有进一步优化的空间。

采用蚁群算法的优化过程包含两个阶段：适应与协作。适应阶段中候选解通过信息素调整解的结构以增强此路径的选择概率；协作阶段则是在候选解的基础上产生更优解。算法先将待求解问题转化成特定格式，然后通过信息素的释放与选择确定决策点，再从全局上规划蚁群的行动方向，多次循环后可求出问题的最优解。

3.1 蚁群算法的数学模型

设蚁群中蚂蚁的总数目是m。蚂蚁k在运动中根据信息素浓度及启发信息计算当前状态的转移概率以确定移动方向。其在t时刻的状态转移概率（t）表示如下：

τij（t）表示t时刻路径＜i，j＞上的信息素量，初始时刻各条路径的信息量相等，即均为等值常数；ηik（t）为启发函数；allowedk表示可供蚂蚁选择的节点集；α表示路径相对重要性的信息启发因子；β表示能见度相对重要性的期望启发因子。每次寻优过程中，信息素的量在数值上可能会远大于启发信息，因此，在每次循环后要对路径＜i，j＞上的信息素量进行如下调整：

ρ表示信息素挥发系数，1－ρ表示信息素残留因子，其取值范围为［0，1）；Δτij表示路径＜i，j＞上的信息数增量。

本文采用蚁群算法解决组合优化问题：

第1步是随机确定Total＿ant只蚂蚁：每一只代表一种组合方案且在创建时便进行评估，通过待优化问题的约束条件筛选出合格的Total＿ant只蚂蚁。为避免陷入局部最优解的情况，因此Total＿ant要稍大，以增加解的多样性。

第2步是将Total＿ant只蚂蚁的目标函数值F（k）的倒数（恒大于0）作为信息素函数的自变量，计算初始信息素及优化过程中解空间各组解的信息素增量，即

其中A为常数，用于调整τ0的数值大小处于合理范围，以便于蚁群算法后续运行；τ（I，J，K）表示K维变量中I点至K＋1维变量中J点路径的信息量；Δτ0（I，J，K，k）表示蚂蚁k由K 维变量中的I点移动到K＋1维中J点路径上的信息素量。

第3步是确定组合优化问题的搜索策略。在搜索阶段，遍历每只蚂蚁在各维变量中的搜索与信息素更新。指定某蚂蚁k在K维搜索，其在其它维度变量上的组合优化值不变，只改变第K维变量中J的值，同时计算第K维变量中的变量值为J时的启发函数。参照式（1）计算状态转移概率P（I，J）：

其中JKmax表示第K维中变量值的个数，从中选出转移概率最大值对应的J值以替换蚂蚁k在第K维变量中值达到修改蚂蚁k的组合方案。τ（I，J，K）信息量的更新按如下过程进行：

其中τ＃（I，J，K）为此路径更新前的信息素；A1为常数。按照上述流程即可完成对所有蚂蚁在所有维度上的搜索过程，此流程遍历一次记为一次全局寻优搜索。

第4步是确定优化的停止条件。由于蚁群算法属于直接搜索策略，因此其值的组合解均是有效的优化解。在本次优化中选取最大寻优搜索循环次数作为停止条件。

3.2 舯剖面结构优化

对于本船，假定船底结构、舷侧结构及甲板结构的纵骨间距相等，以总纵强度为约束条件，优化舯剖面的板和纵骨组成的板格。优化的设计变量选取舯剖面的板厚、纵骨间距与骨材截面，如表5和图6所示。

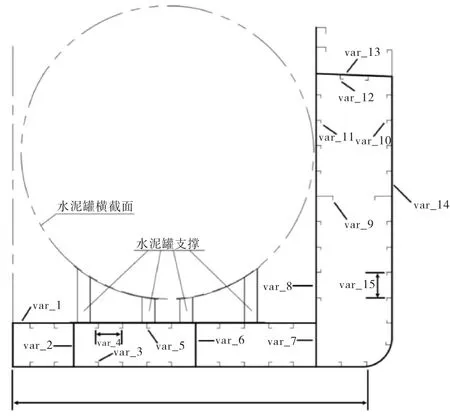
图6 舯剖面优化变量选取示意图

表5 舯剖面优化变量表

由于优化的目标是货舱区域的结构重量，因此选取舯剖面纵向构件所构成的网格模型的重量最轻为目标函数。优化目标取舯剖面构件面积和SALL，优化目标即为求SALL的最小值：

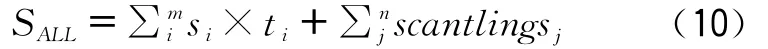
m，n为舯剖面板单元数、纵骨数；si为纵骨间距；ti为单元厚度；scantlingsj为骨材截面积。

在此次优化中，取A、A1为5；信息启发因子α＝4；期望启发因子β＝1；挥发系数ρ＝0.5；蚂蚁数Total＿ant＝40。优化8次后，优化结果如表6所示。

减重量＝2 743.13－2 456.67＝286.46（kg）

减重百分比＝286.46／2 743.130×100%＝10.44%

按空船重量1 067.40t计算，船体结构重量约为700t，由此可求该船型优化后可节省钢料约70t，经济效益可观。

表6 舯剖面优化前后对比表

4 结语

本文通过有限元直接计算校核罐装水泥船船体结构，并通过蚁群算法优化船体结构，得到如下结论：

（1）罐体间甲板采用非刚性连接方式，能阻断总纵载荷传递，对于改善结构局部高应力水平具有较好优势；

（2）通过蚁群算法对货舱区域舯剖面进行了优化，使低应力状态下的船体结构得到减轻，经计算，得出优化后的船体结构单位长度结构重量减轻10.44%，全船减重值约为70t；

（3）船长＞60m、甲板开口宽度＞0.7的散装水泥船已经超出《钢质内河船舶建造规范（2016）》所适用的范围，本文所提供的校核过程、调整方案及结构优化结果，对后续船型的设计工作来说，具有较好的参考价值。