MIKE 21FM二维水流计算模型在桥梁防洪评价壅水计算中的应用

2018-02-27魏炜，谢军，刘芳

西部交通科技 2018年12期

魏炜，谢军，刘芳

（广西交通职业技术学院，广西南宁 530023）

0 引言

随着经济社会的快速发展，铁路、公路等交通网络基础设施越来越多。为了减少经济运行成本，公路、铁路在跨越河道时基本都以架桥方式进行。当桥梁跨越河道时，由于桥墩的存在，会挤占河道的行洪断面，对河道的行洪造成一定的影响。根据水利部发布的《河道管理范围内建设项目管理的有关规定》［1］，其中第五条规定：对于重要的建设项目，建设单位应编制防洪评价报告。

壅水计算是桥梁防洪评价报告中的关键内容，是分析工程建设对河道演变、堤防稳定、防汛抢险、行洪度汛的依据。在桥梁防洪评价报告审查中，历来受到审查专家的重点关注。据调查［2］，桥梁设计部门的壅水计算大多采用经验方法，不同的编制单位有不同的结果，使审查者难以判断其计算成果的合理性。为了使桥梁计算成果更加准确、合理，本文尝试用丹麦水力研究所研制的MIKE 21FM二维水流计算模型对桥梁所在河段的河道水流进行模拟计算，并通过一维的河道水面曲线进行率定，分析其合理性。

1 MIKE21计算方法及原理

MIKE 21是DHI（Danish Hydraulic Instititute，丹麦水力研究所）所研发，专门用于模拟河流、湖泊、河口、海湾、海岸以及海洋的水流、波浪、泥沙及环境的工程软件包。为了研究桥梁建设前后河道不同位置的水位变化情况，本文采用丹麦水力研究所研制的MIKE 21FM二维水流计算模型对不同水文条件下的河道水流进行模拟计算。

1.1 计算原理

MIKE 21FM二维水流计算模型建立在二维数值求解方法的浅水方程基础上，深度上集成不可压缩雷诺平均Navier－tokes方程。在水平面里可以使用笛卡尔坐标和球面坐标。原始方程的空间离散使用单元中心的有限体积法，空间域由连续离散细分成非重叠的三角形或四边形非结构化网格单元。对流通量的计算采用Riemann近似求解，可方便处理非连续的解决方案，时间积分采用显式积分方法。本次模型采用非结构三角形网格单元，非常利于对复杂边界进行拟合，利用干湿网格判断法处理移动边界，方便快捷。

1.2 计算方法

模型计算方法为采用单元中心的有限体积法对二维浅水控制方程组求解。对于浅水方程，整合水平动量方程和连续方程，在水深上h＝η＋d，可得到二维浅水方程：

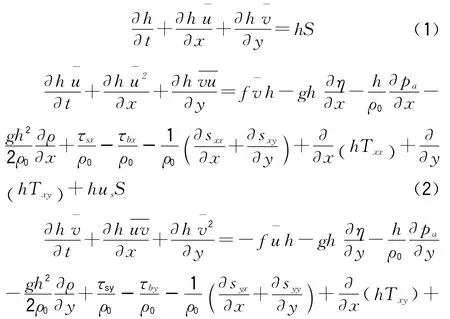
其中：t是指时间；x，y，z为右手Cartesian坐标系；d为静止水深；h＝η＋d为总水深；η为水位；u，v，w分别为流速在x，y，z方向上的分量；ρ为水的密度，ρ0则是参考水密度；pa为当地的大气压；f＝2Ωsin，为参数（是地球自转角速率，为地理纬度）；CoriolisΩ 和为地球自转引起的加速度；sxx、syy、syx、syy为辐射应力分量；Txx、Txy、Tyx、Tyy为水平粘滞应力项，S 为源汇项，（us，vs）源汇项水流流速。

横线表示深度的平均值。例如，u和v是平均深度和平均速度，被定义为：

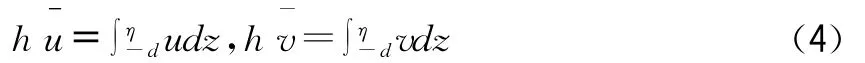
横向上Tij包括粘滞摩擦，动荡的摩擦和差别平流。他们的估测使用的是一种基于平均深度流速梯度的涡粘性公式：

1.3 定解条件

1.3.1 边界条件

开边界：

ηr为开边界r上已知水位、流速过程。

闭边界：

（1）进口边界条件：进口开边界采用上游来流过程：

Qin（t）为开边界上流量，防洪评价报告壅水采用设计洪峰流量计算。

（2）出口边界条件采用下游的水位或水位～流量关系确定。

（3）陆地边界：根据流体固壁不可穿越的原理，在不考虑渗透的情况下，可以认为陆地边界上法向速度为零；根据水流无滑动原理，水体在陆地边界上的切向流速也应为零。

1.3.2 初始条件

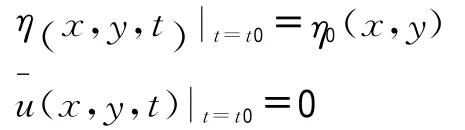
η0为计算初始时刻水位空间分布函数。

2 工程实例研究

2.1 工程概况

宝贤中桥位于大新县城南部，主要跨越河沟为向水河南段。桥址周围为旱地、草丛，地面标高为241.9～244.8m。桥位处河沟明显，现状向水河宽约65m，河道平缓顺直，水流平稳，河道内的地形比较规则，断面属于梯形规则断面，河道底部主要坡降约为0.342‰。桥梁距离上游主流河道大新水文站约为3 000m，本次计算收集了大新水文站1959－2015年的历年洪水资料，桥位下游300m处有一条小支流。根据向水河现状地形地貌，宝贤中桥桥梁中心桩号为K2＋740，（20＋40＋20）m简支预应力钢筋混凝土小箱梁，交角90°，桥面宽44.26m，桥长87m。桥台采用桩柱台，桥墩为柱式墩，墩台均为钻孔桩基础。桥梁方案立面图见图1。

图1 桥梁布置方案立面图（cm）

2.2 模型的计算区域及概化

根据大桥工程所处河段的特点选择模型计算区域河道长约2 800m。模型计算河段上边界在位于大新水文站下游约2 000m处；下边界为拟建桥梁工程下游1 500m处。基于该河段1∶5 000的水下地形图，综合考虑计算区域面积、地形特点以及涉水工程尺寸等因素，采用非结构三角形网格进行剖分，为使网格大小与工程实际尺寸一致，对桥墩附近的局部河段进行加密处理。剖分后三角网格总数共计4 720个，其中河道范围内的网格为非结构网格，进行自由划分，然后光滑处理，平均每个网格长度约为3.0m。计算地形资料采用向水河实测地形图，计算网格及区域数字化地形图见图2和图3。

图2 计算网格划定云图

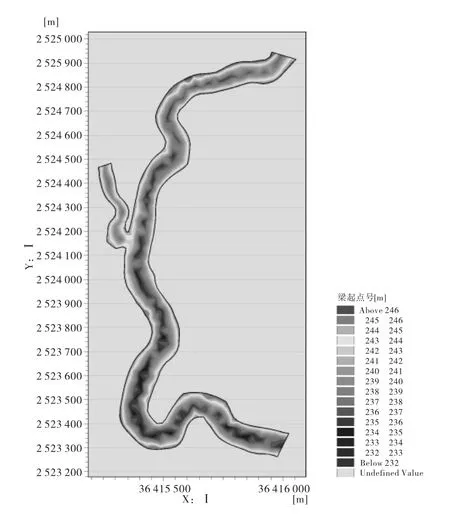
图3 区域数字化地形云图

2.3 模型计算合理性的率定

本次计算的模型验证以桥位下游1 500m断面水位作为控制值，各种水文条件下，河道糙率值取为0.03～0.045。由于桥梁所在向水河是一条流域面积不是很大的小河流，故而模型率定选择主流流量为600m3／s、支流流量为15.32m3／s，水位率定结果见表1 和图4。

表1 水面线率定成果表

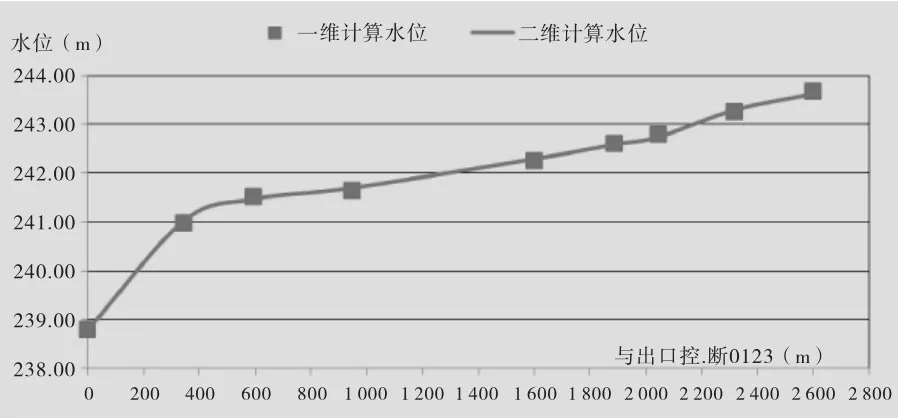
图4 水面线率定成果图

模型率定结果表明，一维计算水位与MIKE 21FM模型计算水位值偏差在0.06m以内。因此，在一定可控误差范围内，一维计算与MIKE 21FM模型计算模拟结果相互吻合较好，模拟精度能够满足对本河段洪水分析计算的要求。

2.4 计算方案及水文条件

为了比较不同洪水情况下桥墩对行洪的影响，本次分别考虑发生100年一遇洪水，50年一遇洪水和10年一遇洪水的情况，共计3个方案，对每个方案交通桥修建前后的洪水水位进行分析比较。

河段水流模拟计算条件为上边界采用设计洪水流量，下边界采用出口处洪水位。采用矩法计算历年洪水系列统计参数，并用P－Ⅲ型曲线适线计算设计洪水流量。各方案的上下游边界条件见表2。

2.5 测点的布设及计算结果

为了方便分析工程前后的具体变化情况，在模拟计算水域布设一系列采样点，统计这些采样点在拟建工程建设前后的水位及差值，整理相关数据统计表，并制作等值线图，在此基础上综合分析拟建工程对其所在水域水位的影响。

本次沿河道43个断面的深泓线、两岸分别布置了采样点，用于对整个河段流态的总体分析，采样点布设情况见图5；各计算方案采样点计算值统计结果见下页表3～5（为了方便表述具体的变化情况，表中水位数值保留到小数点后3位），不同洪水情况设计时工程建设前后水位差值云图见下页图6～8。

图5 采样点布设情况示意图

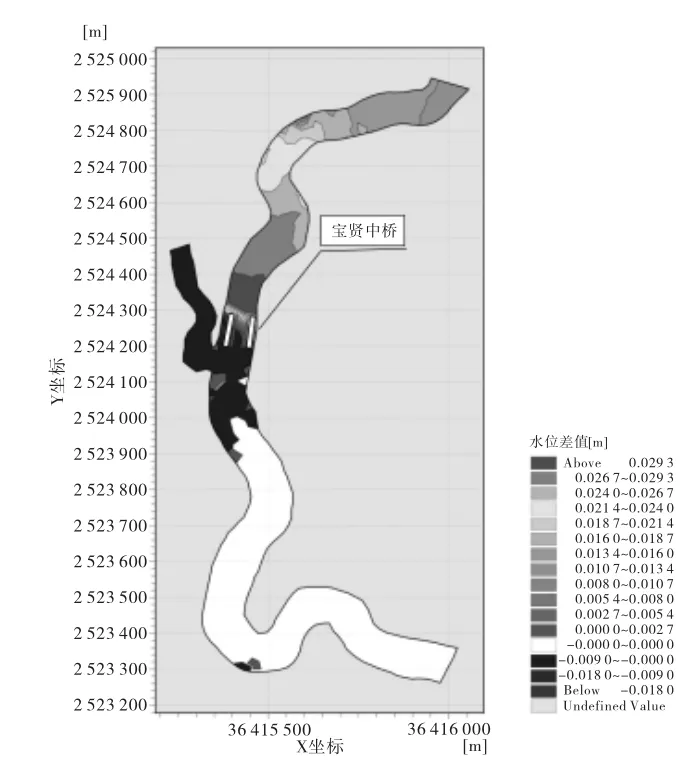
图6 100年一遇水位差值云图

图7 50年一遇水位差值云图

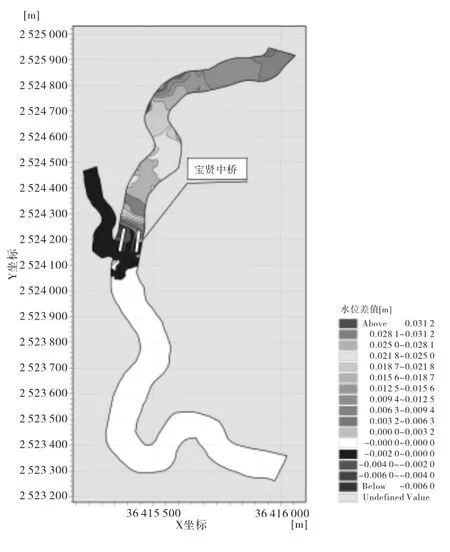
图8 10年一遇水位差值云图

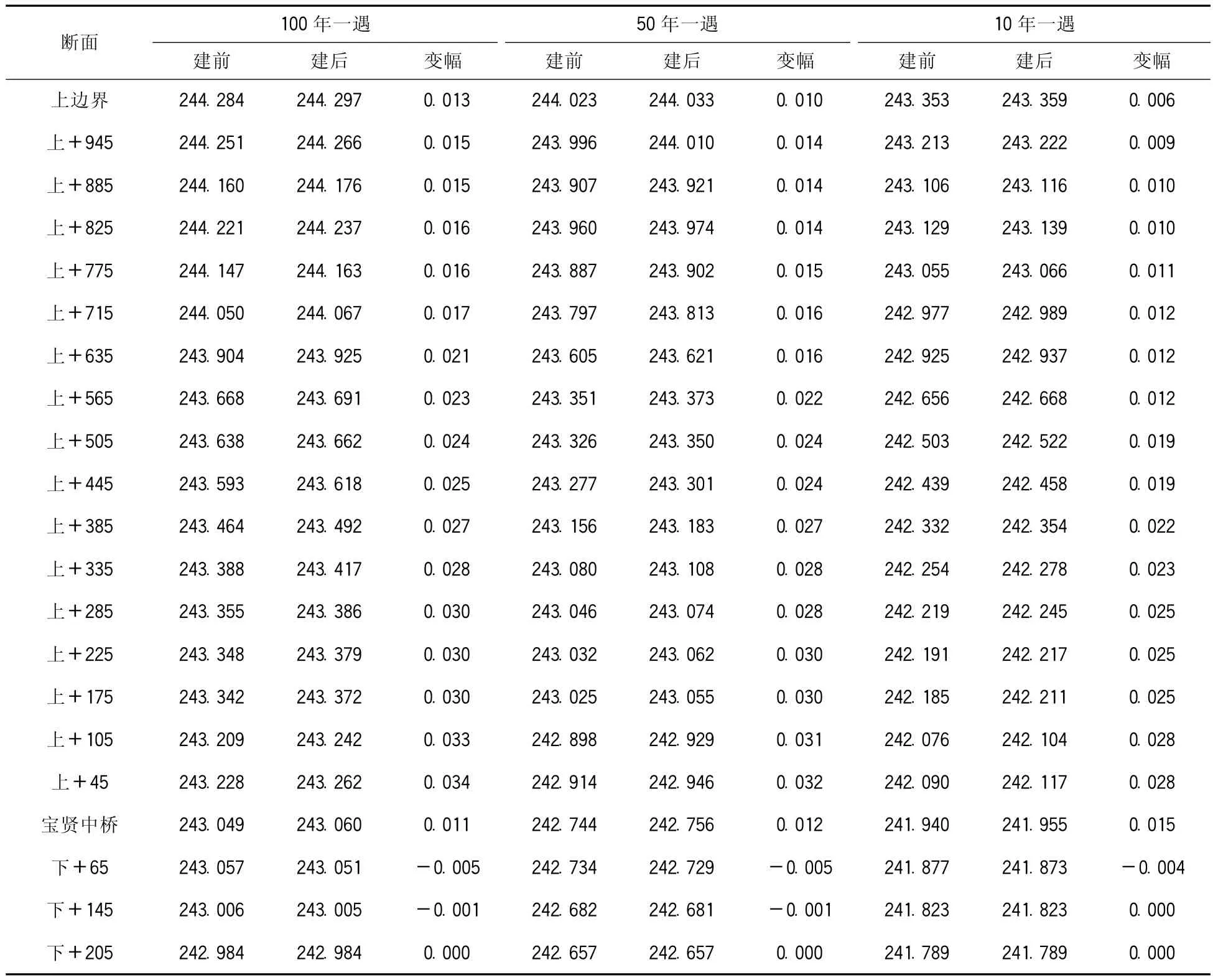
表3 桥梁建设前后右岸水位计算成果表（m）

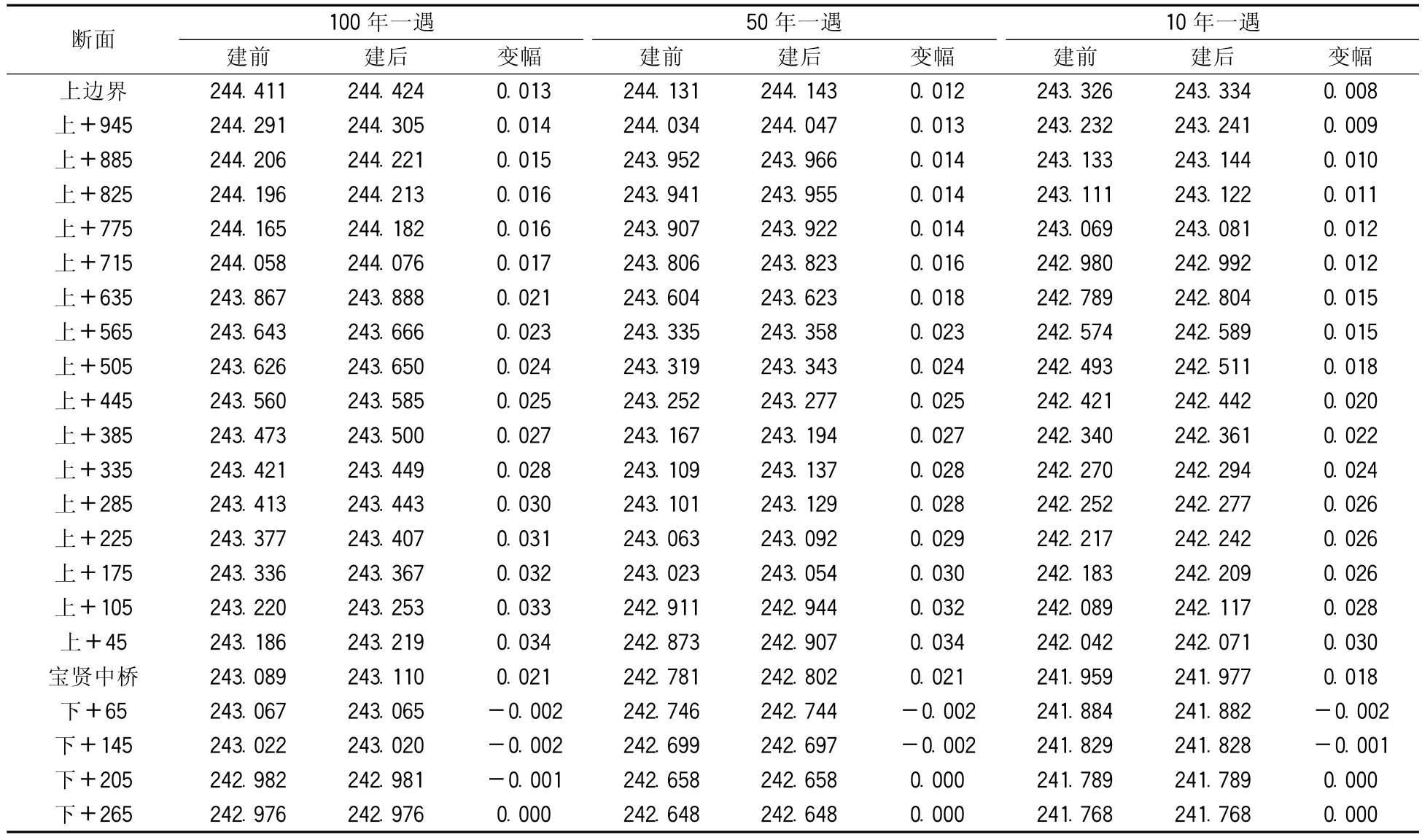
表4 桥梁建设前后深泓线水位计算成果表（m）

表5 桥梁建设前后左岸水位计算成果表（m）

通过对水力计算结果的统计，我们可以定量地分析拟建工程对其所在水域水流产生的影响以及影响分布的状况、程度和范围，特征数据主要包括最大水位壅高值、水位变化相对较大值及其所涉及范围等内容。图6～8分别反映了拟建工程所在水域内平面上各点的水位变化情况。

由表3～5和图6～8可知：桥梁工程建成后，计算水域水位变化都不是平顺衔接的，拟建桥梁工程的上游河道中水位呈壅高现象，在该桥梁工程下游约200m以内的主流河道水位呈降低现象，而由于下游水位降低，导致建桥后支流的水位随之降低。通过模型学计算，可以得知100年一遇洪水方案下河道内水位变化最为明显。以该工况方案下河道内深泓线上的水流来看，上游壅水从拟建桥梁墩前壅水最大0.034m一直递减到河道入口断面处0.013m；下游在拟建桥梁后约200m范围内，河道水位降低均在0.001～0.002m左右，而支流300m范围内，水位降低均在0.005m左右。

因此，综合分析情况可以发现，在百年一遇大洪水范围内，拟建桥梁对河道内的水位影响在0.04m以内。