基于空间分布弹性模量的快速动网格方法

仲继泽,谢志强,沈渡,徐自力

(1.中国舰船研究设计中心船舶振动噪声重点实验室,430064,武汉;2.西安交通大学机械结构强度与振动国家重点实验室,710049,西安)

基于动网格的流固耦合方法可以借助目前已成熟的CFD和CSD商业软件进行流场分析和结构振动计算,从而省去繁重的代码开发工作,目前的动网格技术已能够处理二维及三维网格变形问题,已经广泛应用在工程实际的具有复杂气动外形的结构流固耦合问题的研究中[1]。

在众多流场动网格方法中,弹性体动网格法符合工程实际中结构流固耦合振动多为弹性变形的物理实际,容易产生高质量的动网格[2]。弹性体法最早由Tezduyar提出并发展,将流场网格所包围的空间区域视为虚拟弹性体,采用单一的弹性模量值,以流场网格作为虚拟弹性体的空间离散网格,然后通过有限元方法构建虚拟弹性体变形的静力平衡方程,通过求解该方程计算网格变形后网格节点新的位置坐标[3]。但是,工程实际结构的流场网格的规模一般都在百万量级,所以弹性体法构建的静力平衡方程的规模一般比较庞大,网格变形的计算会占用大量的计算资源[4]。本课题组在Tezduyar的研究工作的基础上,提出一种基于单一弹性模量的快速动网格方法[5-6],构建了结构-虚拟弹性体的整体动力学方程,然后通过振型截断方法计算结构和流场网格节点的位移,其计算量只有Tezduyar的弹性体法的万分之一。本课题组在后续的研究中发现,该快速动网格方法对微小变形问题的适用性很好,但是当结构变形较大时,会造成流场边界层网格的扭曲,使得网格质量降低。

为了解决基于单一弹性体的快速动网格方法的网格扭曲问题,本文借鉴文献[7-8]中提高弹性体动网格方法网格变形质量的做法,引入空间分布弹性模量以改进上述快速动网格方法,提出了一种基于空间分布弹性模量的快速动网格方法。采用改进后的快速动网格方法计算了较大变形条件下的标准弹性梁和Agard Wing 445.6的流场网格变形,并对比了快速动网格方法改进前后对流场网格变形质量的影响。

1 基于单一弹性模量的快速动网格方法的网格扭曲问题

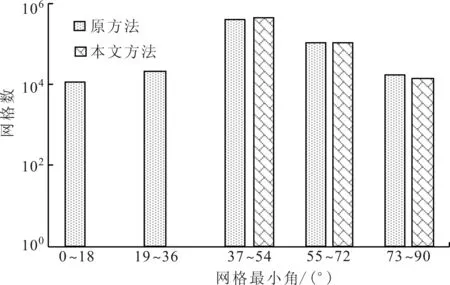
为了准确模拟边界层的流动,流场网格一般在结构表面附近分布比较密集,网格尺寸较小,在远离结构的地方网格尺寸较大。基于单一弹性模量的快速动网格方法不考虑流场网格的大小随空间分布发生变化的实际情况,对于整个虚拟弹性体设定单一的弹性模量,当结构变形较小时网格变形质量是可以保证的,但是当结构变形较大时边界层的尺寸较小的网格可能产生扭曲,使得网格变形质量降低。图1给出了采用基于单一弹性模量的快速动网格方法对标准弹性梁流固耦合问题[9]的流场网格变形情况,可以看出,随着弹性梁最大位移的增加,变形后的流场网格最小角均呈现逐渐减小的趋势,而且模态阶数越高减小的速度越快。在发生第1阶弯曲变形的情况下,弹性梁最大位移为0.07 m时,变形后流场网格最小角为0°。

图1 变形后网格最小角与弹性梁最大位移的关系

弹性梁右端的流场动网格变形后会出现非法网格的情况,如图2所示。

图2 网格变形后出现非法网格的情况

2 基于空间分布弹性模量的快速动网格方法

为了解决基于单一弹性体的快速动网格方法的网格扭曲问题,本文借鉴文献[7-8]中提高弹性体动网格方法网格变形质量的做法,引入空间分布弹性模量以改进基于单一弹性模量的快速动网格方法,从而提出了一种基于空间分布弹性模量的快速动网格方法。本文通过流场网格的大小在空间的分布设定虚拟弹性体的弹性模量的空间分布

(1)

对于第i个流场网格,其内部的虚拟弹性体的应力与应变之间满足胡克定律

σ=2Gε+λδε

(2)

式中:σ为虚拟弹性体的应力张量;ε为虚拟弹性体的应变张量;δ为克罗内克尔符号;拉梅常数G、λ分别为

(3)

(4)

其中ν为虚拟弹性体的泊松比。

将每一个网格单元视为一个有限单元,那么虚拟弹性体的整体的总位能等于所有有限单元位能的总和。虚拟弹性体总位能的有限元形式为

(5)

对于整个虚拟弹性体,其总位能满足最小位能原理

δΠ(Xg)=0

(6)

化简后得到

KgXg=Fs

(7)

对于流固耦合问题,通常将结构对虚拟弹性体的作用视为位移条件,所以上述Fs=0,那么基于空间分布弹性模量的虚拟弹性体变形的静力平衡方程可以写成如下形式

KgXg=0

(8)

参考基于单一弹性模量的快速动网格方法[5-6],将结构振动方程和虚拟弹性体的静力平衡方程结合流固耦合面的位移插值方程,通过数学推导得到结构-虚拟弹性体系统的振动方程,然后通过模态叠加计算结构和流场网格节点的位移,以达到快速计算流场网格变形的节点位移的目的。

本文采用空间分布的弹性模量使得流场边界层的体积较小的网格内部的虚拟弹性体的弹性模量较大,使得远离边界层的体积较大的网格内部的虚拟弹性体的弹性模量较小,而且虚拟弹性体的弹性模量随网格体积的增加以指数规律减小。当流场网格随结构振动发生变形时,边界层网格会随着结构振动作整体的运动,从而避免边界层的流场网格在变形过程中由于挤压、拉扯、扭转引起的网格质量降低的问题。

对于不会产生非法网格的工况,本文方法与单一弹性模量的快速动网格方法的计算速度和精度基本一致。对于产生了非法网格的工况,基于单一弹性模量的快速动网格方法产生的非法网格会使计算无法进行,而本文方法可以避免产生非法网格,顺利进行计算,同时也能保证原有的计算精度和速度。

3 算例验证

3.1 弹性梁的流场动网格

采用本文改进后的快速动网格方法对标准弹性梁流固耦合问题[9]的流场网格变形进行计算得到弹性梁流场网格的变形情况,如图3所示。

(a)网格变形情况

(b)网格变形质量对比图3 弹性梁第1阶弯曲变形时流场网格变形情况

假定弹性梁发生第1阶弯曲振动,当最大位移为0.07 m时,其附近流场网格变形如图3a所示。可以看出,流场网格变形整体比较平顺,弹性梁右端未出现非法网格。变形后流场网格最小角的分布情况如图3b所示,采用本文方法变形后流场网格最小角维持在67°以上,而采用改进前的快速动网格方法计算得到的弹性梁最大位移为0.07 m时网格变形后的网格最小角为0°,此时的流场网格已经成为非法网格。

3.2 Agard Wing 445.6的流场动网格

采用本文方法对三维的Agard Wing 445.6颤振问题[10]的流场网格变形进行计算得到机翼流场网格的变形情况,如图4、图5所示。

假定机翼以第1阶模态振动,当最大位移为24 cm时,流场网格变形如图4a所示。可以看出,流场网格变形整体比较平顺。变形后流场网格最小角的分布情况如图4b所示,采用本文方法变形后流场网格最小角维持在36°以上,而采用改进前的方法得到的网格变形后的网格最小角为0°,是非法网格。

(a)网格变形情况

(b)网格变形质量对比图4 Agard Wing 445.6第1阶弯曲变形时流场网格变形情况

假定机翼以第2阶模态振动,当最大位移为12 cm时,其附近流场网格变形如图5a所示,变形后流场网格最小角的分布情况如图5b所示,采用本文方法变形后所有网格最小角依然维持在36°以上,而采用改进前的快速动网格方法计算得到的机翼最大位移为12 cm时网格变形后的网格最小角为0°,此时的流场网格已经成为非法网格。

(a)网格变形情况

(b)网格变形质量对比图5 Agard Wing 445.6第1阶扭转变形时流场网格变形情况

4 结 论

本文针对基于单一弹性模量的快速动网格方法的网格扭曲问题,参照弹性体方法中提高网格变形质量的方法,提出了一种基于空间分布弹性模量的快速动网格方法。采用本文的方法对标准弹性梁流固耦合问题和Agard Wing 445.6颤振问题的流场网格变形进行了计算,发现当单一弹性模量的快速动网格方法的网格变形出现非法网格(网格最小角为0°)时,本文方法得到的弹性梁流场网格变形后的最小角均维持在67°以上,得到的机翼流场网格变形后的最小角均维持在36°以上,解决了原快速动网格方法的网格扭曲问题。

[1] DOWELL E H. Some recent advances in nonlinear aeroelasticity: fluid-structure interaction in the 21st century [C]∥Proceedings of the AIAA Structures, Structural Dynamics, and Materials Conference. Reston, VA, USA: AIAA, 2010: 1-7.

[2] 张伟伟, 高传强, 叶正寅. 气动弹性计算中网格变形方法研究进展 [J]. 航空学报, 2014, 35(2): 303-319. ZHANG Weiwei, GAO Chuanqiang, YE Zhengyin. Research progress on mesh deformation method in computational aeroelasticity [J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(2): 303-319.

[3] TEZDUYAR T E. Stabilized finite element formulations for incompressible flow computations [J]. Advances in Applied Mechanics, 1991, 28(C): 1-44.

[4] ZHOU X, LI S. A new mesh deformation method based on disk relaxation algorithm with pre-displacement and post-smoothing [J]. Journal of Computational Physics, 2013, 235(2): 199-215.

[5] 仲继泽, 徐自力, 陶磊. 基于虚拟弹性体的快速动网格方法 [J]. 西安交通大学学报, 2016, 50(10): 132-138. ZHONG Jize, XU Zili, TAO Lei. An efficient dynamic mesh method based on pseudo elastic solid [J]. Journal of Xi’an Jiaotong University, 2016, 50(10): 132-138.

[6] ZHONG Jize, XU Zili. A modal approach for coupled fluid structure computations of wing flutter [J]. Proceedings of the Institution of Mechanical Engineers: Part G Journal of Aerospace Engineering, 2017, 231(1): 72-81.

[7] STEIN K, TEZDUYAR T, BENNEY R. Mesh moving techniques for fluid-structure interactions with large displacements [J]. Journal of Applied Mechanics, 2003, 70(1): 58-63.

[8] HUO S H, WANG F S, YAN W Z, et al. Layered elastic solid method for the generation of unstructured dynamic mesh [J]. Finite Elements in Analysis and Design, 2010, 46(10): 949-955.

[9] TUREK S, HRON J. Proposal for numerical benchmarking of fluid-structure interaction between an elastic object and laminar incompressible flow [M]. Berlin, Germany: Springer, 2006: 371-385.

[10]YATES E C J. AGARD standard aeroelastic configurations for dynamic response [J]. European Psychiatry, 1987, 25(10): 1596-1597.