认知无线电Underlay模式下MQAM信号的调制识别

刘明骞,李建英,李兵兵,陈钱

(1.西安电子科技大学信息感知技术协同创新中心,710071,西安;2.南京理工大学电子工程与光电技术学院,210094,南京;3.徐州雷奥医疗设备有限公司,221116,江苏徐州)

认知无线电技术是通过频谱共享的方式合理高效的分配使用有限的频谱资源技术[1]。认知无线电频谱共享模式分为overlay频谱共享模式和underlay频谱共享模式。在underlay频谱共享模式下的频谱共享是指次用户在不超过干扰温度的前提下,可与主用户共用频谱资源,从而提高频谱的利用率[2]。在underlay频谱共享模式下,主用户信号和次用户信号为时频域重叠的信号。由于不同的调制方式所对应的干扰温度不同,因此研究underlay频谱共享模式下时频重叠信号调制方式的识别是很有必要的。

目前,对时频重叠信号的调制识别主要集中于直接提取非平稳信号的循环频率特性上。文献[3]提出基于四阶循环累积量的时频重叠PSK调制信号的特征提取方法,该方法在数据足够长、信噪比为10 dB时,可以达到90%以上的识别率,但该方法受载频和码速率等先验信息的估计精度的影响较大。文献[4]针对时频重叠QPSK调制信号和16QAM调制信号,提出了一种利用接收信号高阶循环累积量构建分类特征,用支撑向量机分类实现信号的调制识别,但该方法需要较大的采样数据和一定的训练信号来达到较高的识别率。文献[5]提出一种基于高阶累积量的时频重叠信号的调制识别方法,但该方法在低信噪比下MQAM信号的性能较差。文献[6]结合二阶和四阶循环累积量的循环频率特性和结构特征,提出一种基于循环频率特征的单信道混合通信信号调制识别的方法和实现算法,但是该方法限定不同分量信号的符号率、载频是不同的。文献[7]提出了一种基于循环累积量及其频率特性分析的时频重叠信号的识别方法,但是该方法中16QAM调制信号和64QAM调制信号的识别效果不佳。文献[8]提出一种基于广义自回归建模的同信道多信号的调制识别方法,但该方法仅适用于信号频域可分或部分重叠的情况。

针对上述问题,本文提出一种基于时频图像纹理特征的时频重叠MQAM调制信号的识别方法。该方法首先对接收到的时频重叠信号做关于频率切片小波变换(frequency slice wavelet Transform,FSWT)得到该信号的时频分析图像,并依据FSWT的频率切片性质截取时频分析图像等高图中纹理差异较明显的部分,然后对所截取的图像进行灰度化处理得到所需的二维灰度图像,并提取基于灰度-梯度共生矩阵的图像纹理特征向量,最后利用径向基(radial basis function,RBF)神经网络分类器实现了时频重叠MQAM信号的调制方式的识别。仿真结果表明,本文方法在信噪比为2 dB时,时频重叠MQAM信号的平均识别率可达到94%以上,是一种有效可行的方法。

1 信号模型

在underlay频谱共享模式下,主用户和次用户共享频谱,此时信号为时频重叠信号p(t),可以表示为[2]

(1)

式中:N为用户信号个数;n(t)为高斯白噪声;si(t)表示第i个用户的数字调制信号;si(t)和n(t)之间相互独立。当si(t)为MQAM调制时,可表示为

si(t)=

(2)

式中:p为采样长度;g(t)为成型脉冲函数;fci为载波频率;φ0i为初始相位;Ti为符号周期;ai和bi分别为信号si(t)的同相分量和正交分量,当M=16时,ai,bi∈{±3,±1,},当M=32时,ai,bi∈{±5,±3,±1}且不包含(5,5)、(-5,5)、(5,-5)和(-5,-5),当M=64时,ai,bi∈{±7,±5,±3,±1}。本文待识别的时频重叠信号为时频重叠MQAM信号。

2 调制识别方法

2.1 频率切片小波变换

频率切片小波变换定义为[9]

(3)

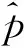
依据帕塞维尔方程,如果σ不是估计频率v的函数,则式(4)可表示为

Ff(t,ω,σ)=

(4)

2.1.1 尺度因子的确定 频率切片小波变换的时频分析特性取决于尺度因子σ的大小。尺度因子σ是时间分辨率和频率分辨率的平衡参数,其选择基于以下的原理[10]:根据Morlet小波变换原理有σ∝ω,可设σ=ω/k,k>0,则式(4)转化为

(5)

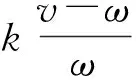
Ff(t,ω,k)=

(6)

由于Heisenberg的不确定原理的限制,不可能使时域分辨率和频域分辨率同时达到最高,只能折中估计σ或k,因此引入2个评价参数来分析时频分辨率:频率分辨率比η=Δω/ω和幅值期望响应比ξ(0<ξ≤1),其中ξ通常取值为21/2/2、0.5、0.25等[11]。下面用狄克拉函数建立不等式,并对尺度因子进行分析。

(1)当p(t)=δ(t-t0)且频率小波变换满足

(7)

和式(6)时,可得到

(8)

即

(9)

(2)当p(t)=exp(jω0t)且频率小波变换满足

(10)

和式(5)时,可得到

|h(σΔt)|≤ξ|h(0)|

(11)

即

(12)

式中:μ是频率变化量与时间变化量的积,即

μ=ΔωΔt

(13)

(14)

从而建立了变换因子k与时频分辨率比η之间的关系。由于σ=ω/k反映了尺度因子σ与k之间的关系,因此可以通过调节k的大小来实现所需的时频分辨率。

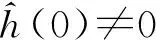
2.1.3 频率切片时频区域选取 由于FSWT具有频率切片的性质,因此所得到的时频分析图像可依据图像的特点自由地截取所需的频率切片,以便于纹理特征的分析。下面以频谱重叠率为20%的双16QAM信号为例,说明频率切片时频区域的选取步骤:①利用式(3)对接收时频重叠信号进行时频分析得到时频分析图像,如图1所示;②对时频分析图像取等高图得到二维图像,如图2所示。由于不同调制类型的时频重叠信号等高图中能量聚集集中的部分存在明显的纹理差异,因而选取图2中能量聚集的频率切片作为提取时频图像纹理特征的对象。在图2中,空白部分表示无信号信息,位置①部分表示信号信息较弱,位置②部分表示信号信息较强,该部分为信号能量聚集的部分。

图1 时频重叠信号的FSWT时频分析图

图2 时频重叠信号FSWT时频分析图的等高图

2.2 图像纹理特征的提取

2.2.1 图像灰度化 彩色图像是由红(R)、绿(G)、蓝(B)三原色组成的,为了便于图像处理,通常将彩色图像转化为灰度图像,即图像的灰度化。在彩色图像中,R、G、B这3个分量值的范围是0～255,可以理解为一个三维的空间直角坐标系,则彩色图像中每个像素的颜色都可以用该空间的一个点来表示;在灰度图像中,R=G=B,则灰度图像的每个像素的颜色值在R=G=B直线上,此时R=G=B的值叫灰度值。彩色图像灰度化一般的方法有分量法、最大值法、平均值法和加权平均法。本文根据人眼对不同颜色的敏感程度的差异,采用加权平均的方法,将3个分量进行加权平均处理,从而得到灰度化图像。灰度值Gray的加权公式为[13]

Gray=0.290 0R+0.587 00G+0.114 00B

(15)

2.2.2 灰度梯度共生矩阵 纹理是图像的一个重要的却很难描述的特性。对于外形相似但由于方向和角度的多样性的呈现的图像实为一类,因此对于提取的同一种特征值应比较接近,图像的旋转不变性的研究对于图像的纹理特性的特征提取就显得尤为重要。本文采用灰度-梯度共生矩阵提取时频图像的纹理特征,在图像纹理特征的提取过程中对于不同旋转角度和方向的变换不敏感,具有较好的纹理特性分析效果。

灰度-梯度共生矩阵的基本原理[14]:灰度-梯度共生矩阵的元素H(x,y)(x=0,1,2,…,Lf;y=0,1,2,…,Lg-1)定义为在归一化的灰度图像F(i,j)及归一化的梯度图像G(i,j)中具有灰度值x和梯度值y的像素数,可表示为

(16)

(17)

式中:gmax和gmin分别表示为梯度图像像素的最大值和最小值;fmax和fmin分别表示为灰度图像像素的最大值和最小值;Lf为图像灰度级;Lg为图像梯度级;x和y由集合{(i,j)|f(i,j)=x,g(i,j)=y;i,j=0,1,2,…,N-1}(N表示灰度值和梯度值的长度)可得;灰度值x=0,1,2,…,Lf-1和梯度值y=0,1,2,…,Lg-1。

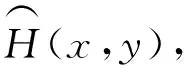
(18)

由式(18)可知,灰度-梯度共生矩阵是将图像灰度信息和梯度信息进行融合,共同表征图像的纹理特性,并且具有较好的旋转不变性,适用于时频图像特征的提取。15个特征从不同角度分析提取时频图像的纹理特性[15]。文献[15]从不同角度提取了15个凸显时频图像纹理特性的特征,在这15个特征中,小梯度优势和大梯度优势反映了灰度图像的灰度信息变化的剧烈程度,即当图像灰度变化平缓时,小梯度像素数多,小梯度优势大,相反当图像的灰度变化剧烈时,大梯度像素多,大梯度优势大;能量反映了图像的灰度分布均匀程度和纹理粗细度;惯性表示凹槽的深度;相关运算反映了图像纹理特征的一致性;混合熵表示非均匀纹理图像的复杂性以及纹理的水平方向和垂直方向的相似性;逆差矩反映图像纹理的同质性,度量图像纹理的局部变化等。本文通过这15个特征计算出灰度图像的特征向量作为识别特征。

2.3 所提方法步骤

综上所述,本文所提出的underlay认知无线电中时频重叠MQAM信号的调制识别方法的具体步骤如下:

(1)利用式(3)对接收到的时频重叠MQAM信号做关于FSWT的时频分析得到时频分析图像;

(2)对时频图像取等高图得到二维图像,并依据FSWT的频率切片性质截取纹理差异较明显的部分;

(3)将截取的部分时频分析图像根据式(15)进行灰度化处理得到所需的二维灰度图像;

(4)对灰度化图像利用15个灰度-梯度相关特征计算其灰度-梯度共生矩阵特征向量;

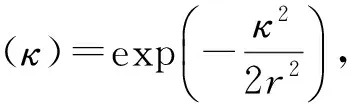
3 仿真及分析

针对本文的时频重叠信号的调制识别方法进行MATLAB仿真实验,时频重叠MQAM信号调制类型为16QAM、32QAM和64QAM,2个时频重叠信号参数设置为:采样频率分别为30 MHz和60 MHz;载频分别为5 MHz和7.6 MHz;码元速率分别为1 MHz和2 MHz。3个时频重叠信号参数设置为:采样频率分别为30 MHz、60 MHz和30 MHz;载频分别为5 MHz、7.6 MHz和10.2 MHz;码元速率分别为1 MHz、2 MHz和1 MHz。采样点数为4 096,采用的观测噪声为高斯白噪声,升余弦脉冲成型函数的滚降系数设为0.35。

实验1 测试在不同信噪比和不同信号个数条件下,本文所提方法的识别性能。实验采用分量信号功率相等且频谱重叠率为20%的时频重叠MQAM信号,实验仿真结果如图3所示。从图3可以看出,随着信噪比的增加,信号的识别率增大,在信噪比大于4 dB时,识别率可以达到90%以上。由此说明,本文所提的识别方法与时频重叠信号的调制类型无关,但是与时频重叠信号的个数有关,时频重叠信号个数越少,识别正确率越高。

图3 不同信号个数下本文方法的调制识别性能

实验2 测试不同的频谱重叠率下,本文所提方法的识别性能。以16QAM双信号时频重叠为例,分量信号功率比为1∶1,频谱重叠率分别为40%、60%、80%和100%,实验仿真结果如图4所示。从图4可以看出,在不同的频谱重叠率下,信噪比大于2 dB时,信号的识别率均可达到95%以上。因此说明,本文方法对频谱重叠率是稳健的。

实验3 测试不同功率比下,本文所提方法的识别性能。以16QAM双信号时频重叠为例,频谱重叠率分别为20%,实验仿真结果如图5所示。从图5可以看出,在不同的功率比下,信噪比大于4 dB时,信号的识别率均可达到95%以上。由此说明,本文方法对分量信号的功率比也是稳健的。

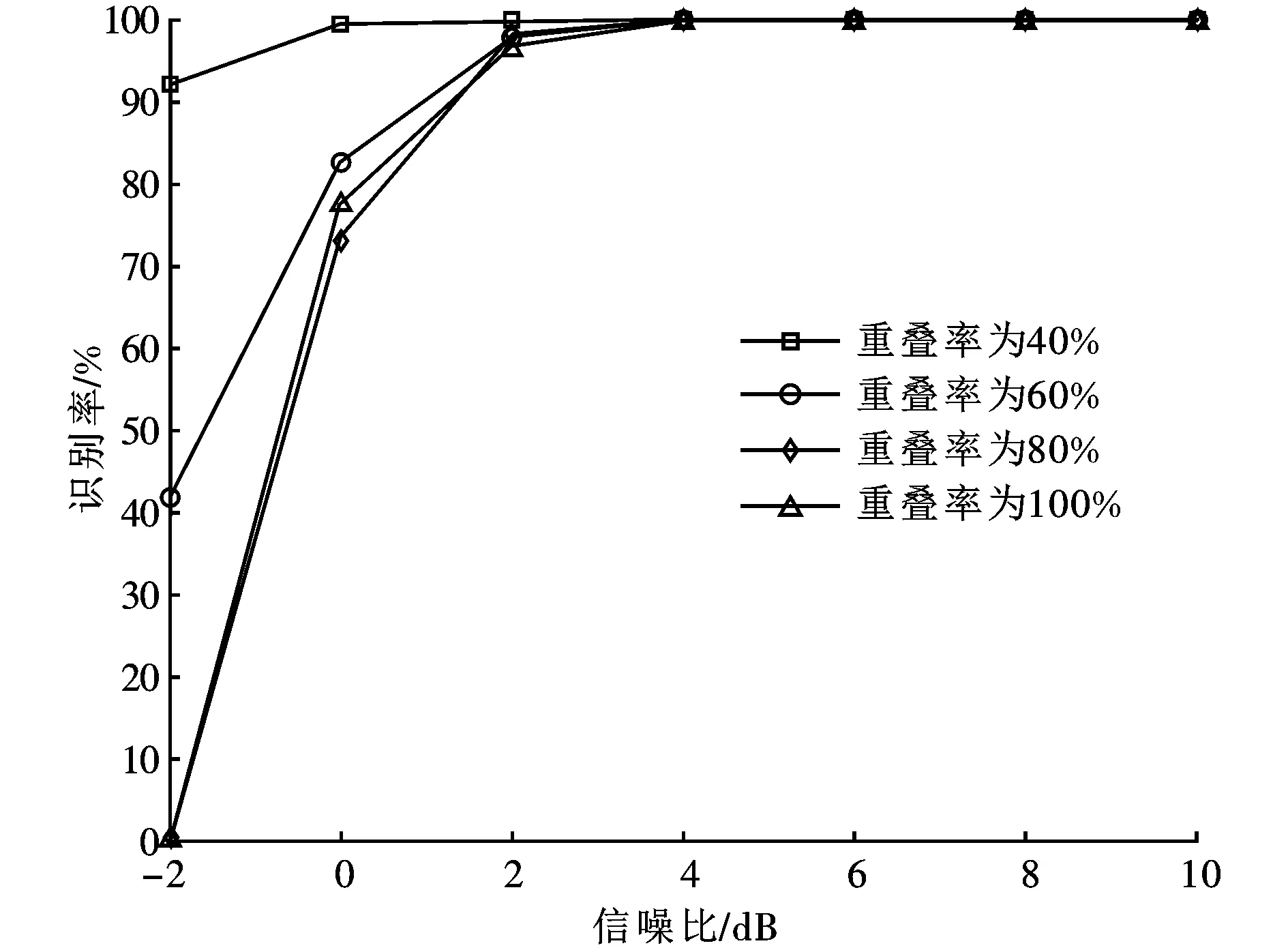
图4 不同重叠率下本文方法的调制识别性能

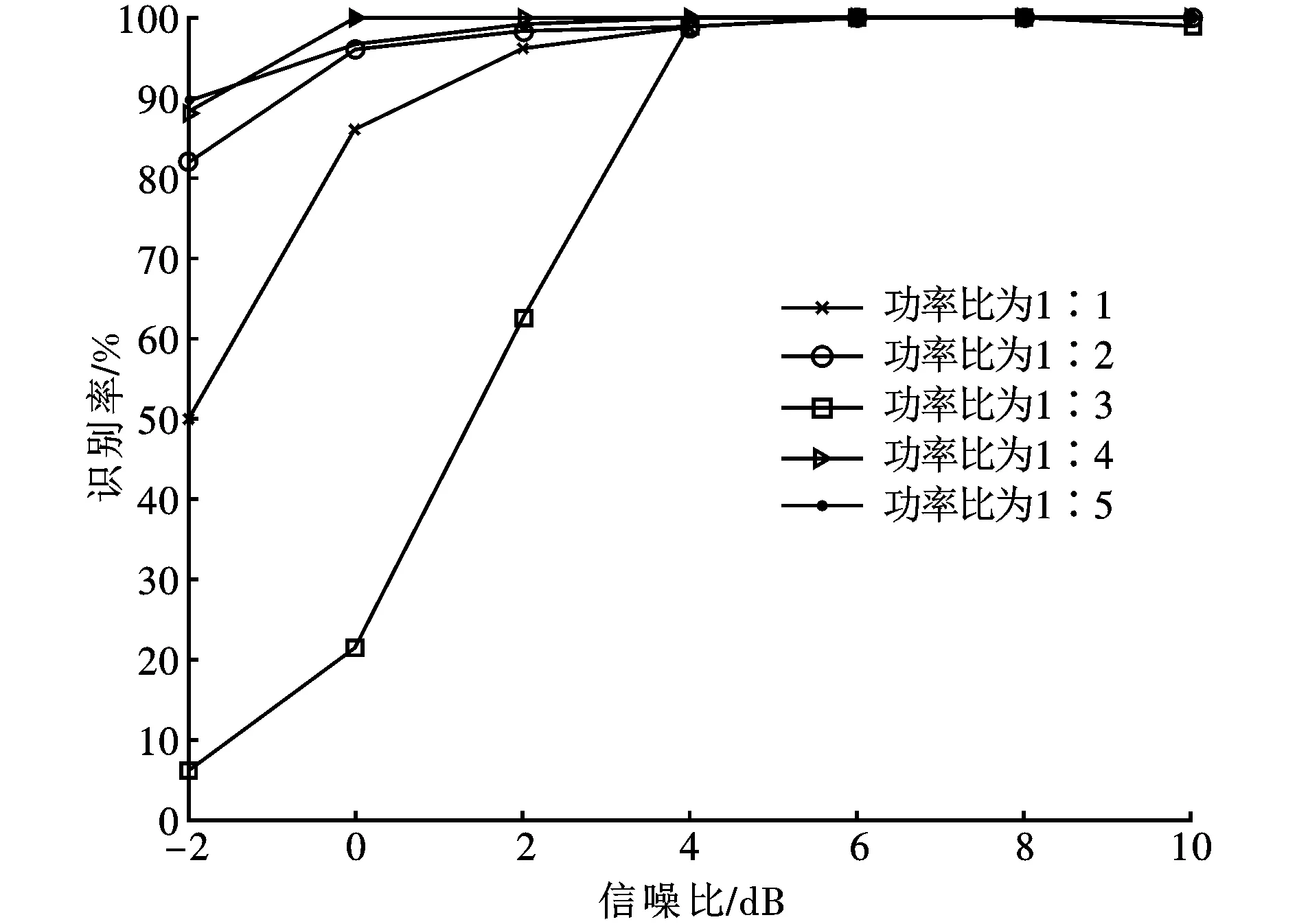
图5 不同功率比下本文方法的调制识别性能

实验4 在相同的实验环境和信号参数设置下,以16QAM双信号时频重叠为例,将本文方法与文献[5]和文献[7]的方法进行对比实验,实验仿真结果如图6所示。从图6中可以看出,在信噪比大于0 dB时,本文的调制识别方法的识别率高于文献[5]和文献[7]方法的识别率,由此说明本文所提方法优于现有的时频重叠信号调制识别方法。此外,本文所提的识别方法的计算复杂度为O(n2)。

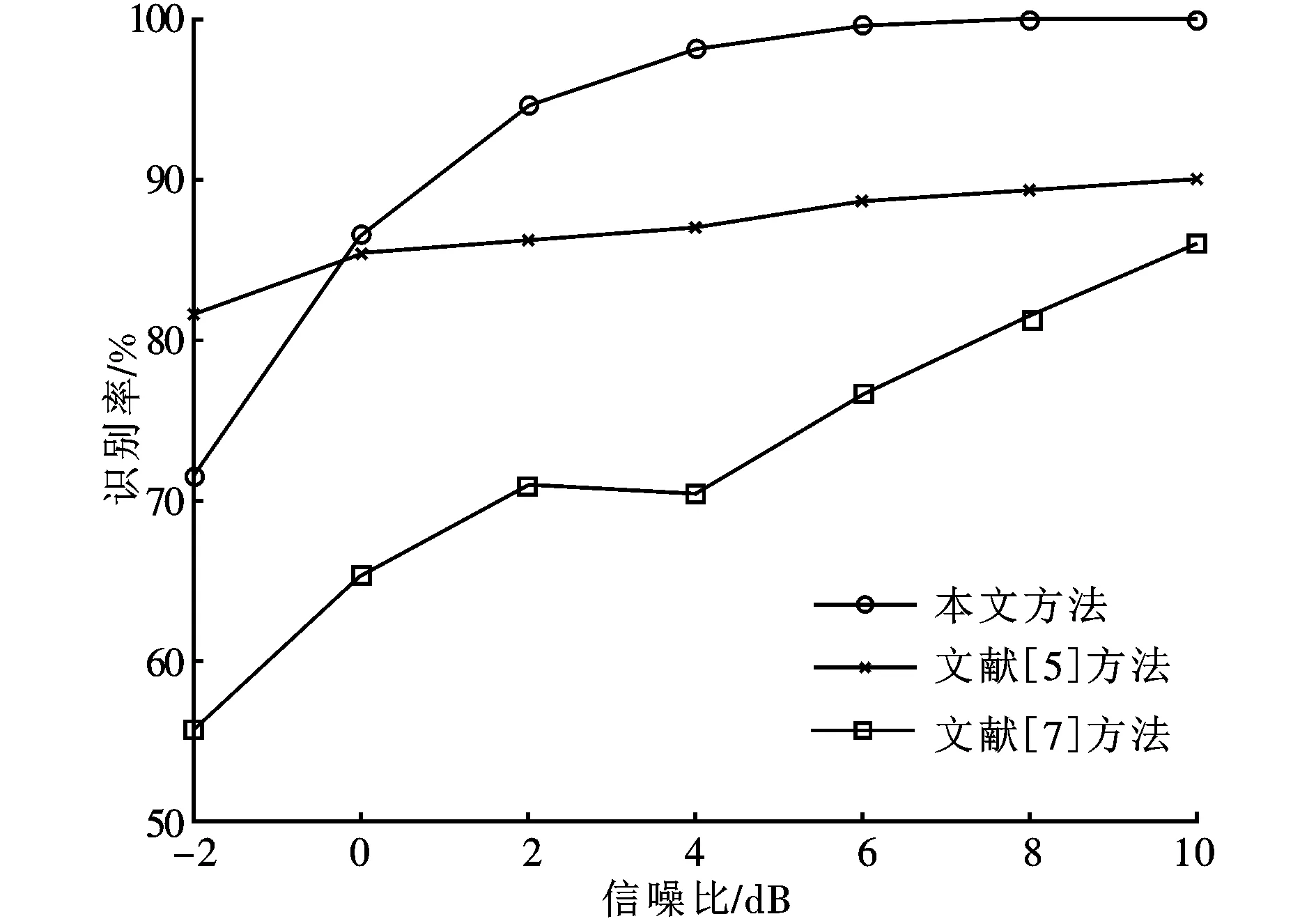
图6 不同调制识别方法的性能对比

4 结 语

本文针对underlay认知无线电中时频重叠的MQAM信号的识别问题,提出了一种基于时频图像纹理特性分析的调制识别方法。首先分析了时频重叠MQAM信号的时频特性,然后通过提取时频图像的纹理特征并使用RBF分类器实现了时频重叠MQAM信号调制类型的识别。仿真结果表明,在低信噪比下,本文方法优于现有的时频重叠信号调制识别方法,并且本文方法对分量信号的功率比和频谱重叠率具有稳健性。

[1] SHI Yaohua, LIU Mingqian, ZHOU Fan. User numbers estimation for underlay cognitive radio [C]∥Proceedings of 6th International Conference on Wireless, Mobile and Multi-Media. London, UK: IET, 2015: 120-123.

[2] WANG Jianghong, LI Bingbing, LIU Mingqian, et al. SNR estimation of time-frequency overlapped signals for underlay cognitive radio [J]. IEEE Communications Letters, 2015, 19(11): 1925-1928.

[3] LI Kuangdai, GUO Lili, SHI Rong, et al. Modulation recognition method based on high order cyclic cumulants for time-frequency overlapped two-signal in the single-channel [C]∥Proceedings of 1st International Congress on Image and Signal Processing. Piscataway, NJ, USA: IEEE Computer Society, 2008: 474-478.

[4] 付海涛, 石荣, 万群, 等. 基于HOCCs和SVM的单通道时频重叠信号调制识别 [J]. 电子信息对抗技术, 2009, 24(6): 14-18. FU Haitao, SHI Rong, WAN Qun, et al. Modulation recognition based on HOCCs and SVM for co-channel time-frequency overlapped signal [J]. Electronic Information Confrontation Technology, 2009, 24(6): 14-18.

[5] 徐闻, 王斌. 采用高阶累计量的时频混叠信号调制识别研究 [J]. 信息工程大学学报, 2013, 14(3): 299-305. XU Wen, WANG Bin. Method of modulation recognition of time-frequency overlapped signals based on high-order cumulants [J]. Journal of Information Engineering University, 2013, 14(3): 299-305.

[6] 赵宇峰, 曹玉健, 纪勇, 等. 基于循环频率特征的单信道混合通信信号的调制识别 [J]. 电子与信息学报, 2014, 36(5): 1202-1208. ZHAO Yufeng, CAO Yujian, JI Yong, et al. Modulation identification for single-channel mixed communication signals based on cyclic frequency features [J]. Journal of Electronics & Information Technology, 2014, 36(5): 1202-1208.

[7] 张洋, 彭华. 单通道混合信号调制识别 [J]. 信息工程大学学报, 2016, 17(6): 662-668. ZHANG Yang, PENG Hua. Modulation recognition for mixed signals in single channel [J]. Journal of Information Engineering University, 2016, 17(6): 662-668.

[8] 陆明泉, 肖先赐. 基于GAR的同信道多信号的调制识别 [J]. 清华大学学报(自然科学版), 2009, 49(10): 1676-1680. LU Mingquan, XIAO Xianci. Modulation recognition of multiple co-channel signals based on GAR [J]. Journal of Tsinghua University (Science and Technology), 2009, 49(10): 1676-1680.

[9] VENKATA SUBBARAO M. Time-frequency analysis of non-stationary signals using frequency slice wavelet transform [C]∥Proceedings of the 10th International Conference on Intelligent Systems and Control. Piscataway, NJ, USA: IEEE, 2016: 7726999.

[10]YAN Zhonghong, MIYAMOTO A, JIANG Zhongwei, et al. An overall theoretical description of frequency slice wavelet transform [J]. Mechanical Systems & Signal Processing, 2010, 24(2): 491-507.

[11]李建伟. 基于频率切片小波变换的轨道交通轮轨振动信号分析 [D]. 南京: 南京理工大学, 2014: 34-37.

[12]WANG Fuge, XING Zongyi, QIN Yong, et al. The analysis of axle box vibration signal based on frequency slice wavelet transform [C]∥2015 International Conference on Computer and Computational Sciences. Piscataway, NJ, USA: IEEE, 2015: 64-69.

[13]贺姣. 基于色差模型的彩色图像灰度化算法研究 [D]. 西安: 西安电子科技大学, 2014: 9-10.

[14]CHEN Shuo, WU Chengdong, CHEN Dongyue, et al. Scene classification based on gray level-gradient co-occurrence matrix in the neighborhood of interest points [C]∥IEEE International Conference on Intelligent Computing and Intelligent Systems. Piscataway, NJ, USA: IEEE, 2009: 482-485.

[15]UBUL K, YADIKAR N, AMAT A, et al. Uyghur document image retrieval based on gray gradient co-occurrence matrix [C]∥Proceedings of 2015 Chinese Automation Congress. Piscataway, NJ, USA: IEEE, 2015: 762-766.

[16]DEY A, SING J K. Face recognition by fuzzy generalized 2DFLD method and RBF neural network classifier [C]∥2015 IEEE Workshop on Computational Intelligence: Theories, Applications and Future Directions. Piscataway, NJ, USA: IEEE, 2015: 7495536.