一类平衡的最优代数免疫度布尔函数的构造
2018-02-27王筱琛陈克非沈忠华程慧洁
王筱琛 陈克非 沈忠华 程慧洁
(杭州师范大学理学院数学系 浙江 杭州 310012)
0 引 言
近年来,代数攻击[1]方法被提出后,受到了密码学界广泛的关注,在密码设计领域就出现了如何设计好的布尔函数来抵抗代数攻击,如何在保证代数免疫度高的前提下保证函数其他密码学性质也不会很差等问题。密码学研究人员致力于研究设计性质优秀的布尔函数来抵抗包括代数攻击在内的攻击手段。近年来,许多最优代数免疫度函数类被密码学者提出[2-8],但是这些函数在达到代数免疫度达到最优的情况下并没有保证其他密码学性质的下界达到一定的高度,比如函数的非线性度、代数次数、平衡性等都没有达到理想的情况。在文献[9]中,作者构造了一类平衡的最优代数免疫度函数,并且拥有最佳代数次数和较高的非线性度,然而它在抵抗快速相关免疫攻击时并没有表现出很好的抵抗能力。文献[10]中作者构造了一类偶数元的非线性度非常高的平衡代数免疫度最优布尔函数,并且通过枚举说明了n≤18时函数的非线性度超过了Carlet-Feng函数[11],而且通过实验验证其非线性度与理论上界非常近。我们知道Carlet-Feng函数时一类非常具有代表性的最优代数免疫度布尔函数,并且在抗击快速代数攻击时也有非常好的表现,只是在函数的显示表示上存在一定得缺陷。
不仅如此,如今许多布尔函数学者致力于研究代数免疫度最优的旋转对称布尔函数。这是一类具有在循环群作用下保持不变性质的布尔函数,这类布尔函数在一定条件下可以具备良好的密码学性质。文献[12]中构造了两类偶数阶的旋转对称布尔函数,在最优代数免疫度的前提下作者还证明了这两类函数具有足够抵抗线性攻击的代数次数以及非常高的非线性度。还有一些学者利用文献[13]中Ding提出的多数函数,构造最优代数免疫度布尔函数。在文献[5]中证明了多数函数被证明具有最优代数免疫度,并且得到了n元多数函数代数次数为2|log2n|,但是根据Lobanov界[14],多数函数的非线性度是最坏的。因此有许多在多数函数基础上构造的旋转对称布尔函数被提出[15-16],但是在非线性度上面并没有巨大的突破。
本文利用文献[10]中的方法构造了一类偶数元的代数免疫度最优布尔函数,这类布尔函数是由一列多数函数和一个平衡的旋转对称的代数免疫度最优布尔函数串联而成,并且从理论上证明了这类函数的非线性度下界,以及代数次数下界。最后我们还简单分析了函数的相关免疫阶数, 函数是否具有更高的阶数还需进一步研究。
1 准备知识
1.1 布尔函数的基本知识
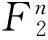
f=[f(0,…,0),f(0,…,1),…,f(1,…,1)]
我们将所有n元布尔函数组成的集合记作Bn,那么对任意f∈Bn,我们可以将其唯一地写F[x1,x2,…,xn]上的多项式:
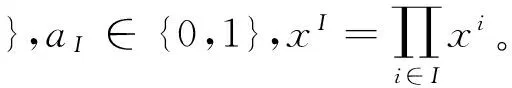
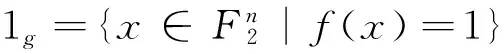
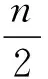
对于f,g∈Bn,定义d(f,g)=wt(f-g)为f与g的距离,f与所有仿射函数的最小距离称为f的非线性度,记作nl(f), 也即:
布尔函数的非线性度可以由其Walsh变换来刻画。对于函数f∈Bn,定义f的Walsh变换为:
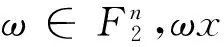
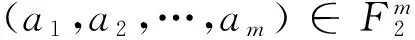
Pr⎣f=a|xi1=a1,xi2=a2,…,xim=am」=Pr[f=a]
则称f是m阶相关免疫函数。
1.2 旋转对称布尔函数
我们称一个布尔函数f∈Bn是对称的,如果对其自变量进行任意的置换,它的值都不变,即:
f(x0,x1,…,xn-1)=f(xτ(0),xτ(1),…,xτ(n-1))
式中:τ是集合{0,1,…,n-1}上的置换。
布尔函数f是对称的当且仅当其代数正规型可以写成如下形式:
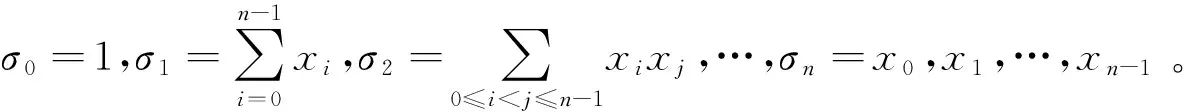
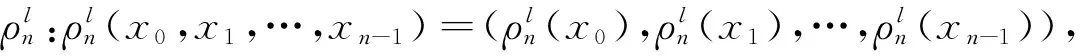
f=⎣f(Λ1),f(Λ2),…,f(Λkn)」
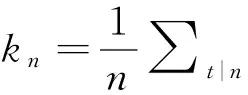
文献[17]中构造了一类偶数阶的具有最优代数免疫度的旋转对称布尔函数:
式中:c∈{0,1}。并且证明了这类函数具有较高的非线性度和代数次数。
1.3 布尔函数的串联表示
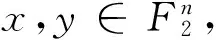
2 函数的构造与性质分析
2.1 函数W(x,y)的构造
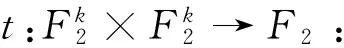
t(x,y)=g(xy2k-2)
为bent函数,且这个函数属于Dillon在文献[18]中提出的PSap类函数。并且在文献[19]中证明了如果下面的假设成立,t(x,y)也是代数免疫度最优布尔函数。
假设1对于x∈Z2k-1,x可被表示成长度为k的二元串,若wt(x)表示x的二元串表示中1的个数, 令:
Sr={(a,b)|a,b∈Z2k-1,a+b≡r(mod2k-1),wt(a)+wt(b)≤k-1}
这里1≤r≤2k-2,k≥2,那么|Sr|≤2k-1。
假设的正确性现在还是公开问题, 文献[19]中通过利用一种矩阵变换的算法已经证明了这个假设在k≤29时均成立。
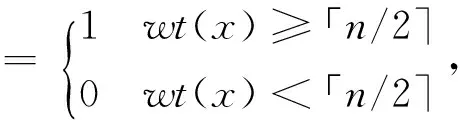

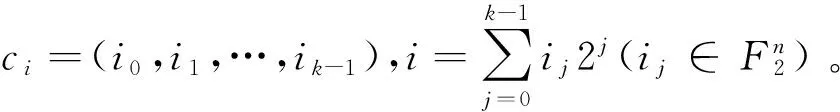
下面将上面函数改写,令:
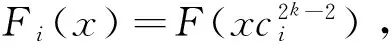
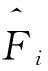

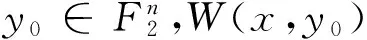
2.2 函数W(x,y)的代数免疫度
引理1[10]设函数f=f0‖f1‖…‖f2k-1,其中f0为平衡函数,fi(1≤i≤2k-1)为代数免疫度最优布尔函数,那么f为代数免疫度最优布尔函数。
定理1若假设1成立,则函数W(x,y)具有最优代数免疫度。
证明由于多数函数是平衡的代数免疫度最优函数,因此tF(x,y)是bent函数,并且具有最优代数免疫度。因此对于任意的l∈An,我们可以将l写成:
l=l0‖l1‖…‖l2k-1
因为tF(x,y)是bent函数,所以:
d(tF,l)=d(0,l0)+d(F1,l1)+…+
d(F2k-1,l2k-1)=2n-1-2n/2-1
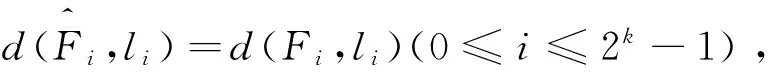

2.3 函数W(x,y)的非线性度
定理2若假设1成立,2k元布尔函数W(x,y)满足不等式:
证明任取l∈B2k,我们有:
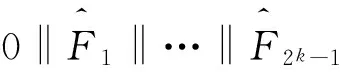
因为d(0,l)≤2k-1,所以:
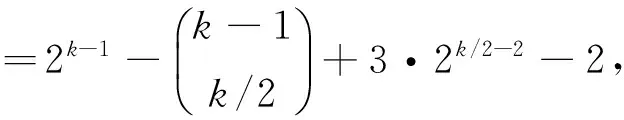
d(W,l)≥d(T,l0)+22k-1-2k≥22k-1-
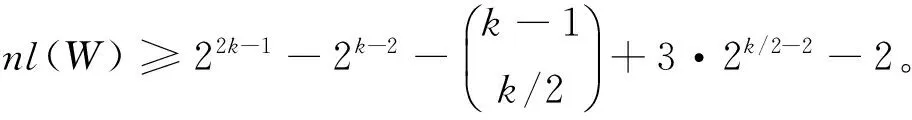
2.4 函数W(x,y)的代数次数
引理2[17]n元旋转对称布尔函数T(x)的代数次数满足:
式中:m为某个正整数。
引理3[5]n元多数函数F(x)的代数次数满足deg(F)=2⎣log2n」。
定理3当k取非2幂次的偶数时,函数W(x,y)的代数次数deg(W)≥n-1。
证明因为
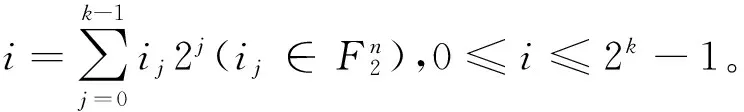
若k为非2幂次整数时,存在m∈N,使得2m+2≤k≤2m+1-1,2⎣log2k」=2m 于是由引理3 所以deg(W)≥n-1。 定理4函数W(x,y)的相关免疫阶tW≥1。 且 于是 又 因此 本文构造了一类偶数元的布尔函数,这类函数在构造方法上运用了函数串联的方法,其中串联因子大部分采用多数函数,在第一个位置的全零函数用一个旋转对称布尔函数来代替,以增加函数的复杂性和改变密码学性质。本文证明了此函数在保证最优代数免疫度的情况下还具有非常高的非线性度和代数次数。并且由于多数函数结构简单,因此在函数生成效率方面也比较有优势。最后我们还对函数的相关免疫阶数进行计算,其是否还具有更高阶的相关免疫阶尚需进一步探索。 [1] Courtois N T,Meier W.Algebraic Attacks on Stream Ciphers with Linear Feedback[M]//Advances in Cryptology-EUROCRYPT 2003.Springer Berlin Heidelberg,2003:345-359. [2] Braeken A,Preneel B.On the Algebraic Immunity of Symmetric Boolean Functions[C]//Progress in Cryptology-Indocrypt 2005,International Conference on Cryptology in India,Bangalore,India,December 10-12,2005,Proceedings.2005:35-48. [3] Carlet C,Dalai D K,Gupta K C,et al.Algebraic immunity for cryptographically significant Boolean functions:analysis and construction[J].IEEE Transactions on Information Theory,2006,52(7):3105-3121. [4] Dalai D K,Gupta K C,Maitra S.Cryptographically Significant Boolean Functions:Construction and Analysis in Terms of Algebraic Immunity[M]//Fast Software Encryption.Springer Berlin Heidelberg,2005:98-111. [5] Dalai D K.Basic theory in construction of boolean functions with maximum possible annihilator immunity[J].Designs,Codes and Cryptography,2006,40(1):41-58. [6] Li N,Qi W F.Construction and Analysis of Boolean Functions of 2t+1 Variables with Maximum Algebraic Immunity[C]//Advances in Cryptology-ASIACRYPT 2006,International Conference on the Theory and Application of Cryptology and Information Security,Shanghai,China,December 3-7,2006,Proceedings.2006:84-98. [7] Li N,Qu L J,Qi W F,et al.On the Construction of Boolean Functions With Optimal Algebraic Immunity[J].IEEE Transactions on Information Theory,2008,54(3):1330-1334. [8] Qu L J,Feng K,Liu F,et al.Constructing Symmetric Boolean Functions With Maximum Algebraic Immunity[J].IEEE Transactions on Information Theory,2009,55(5):2406-2412. [9] Feng K,Liao Q,Yang J.Maximal values of generalized algebraic immunity[J].Designs,Codes and Cryptography,2009,50(2):243-252. [10] Wang Q,Tan C H.Balanced Boolean functions with optimum algebraic degree,optimum algebraic immunity and very high nonlinearity[J].Discrete Applied Mathematics,2014,167(4):25-32. [11] Carlet C,Feng K.An Infinite Class of Balanced Functions with Optimal Algebraic Immunity,Good Immunity to Fast Algebraic Attacks and Good Nonlinearity[M]//Advances in Cryptology-ASIACRYPT 2008.Springer Berlin Heidelberg,2008:425-440. [12] Sun L,Fu F W.Constructions of even-variable RSBFs with optimal algebraic immunity and high nonlinearity[J].Journal of Applied Mathematics & Computing,2017:1-18. [13] Ding C,Xiao G,Shan W.The Stability Theory of Stream Ciphers[M].Springer Berlin Heidelberg,1991. [14] Lobanov M.Tight bound between nonlinearity and algebraic immunity[OL].2005.http://eprint.iacr.org/2005/441.pdf. [15] Fu S,Qu L,Li C,et al.Balanced rotation symmetric boolean functions with maximum algebraic immunity[J].Iet Information Security,2011,5(2):93-99. [16] Fu S,Li C,Matsuura K,et al.Construction of Rotation Symmetric Boolean Functions with Maximum Algebraic Immunity[M]//Cryptology and Network Security.Springer Berlin Heidelberg,2009:402-412. [17] Su S,Tang X.Construction of rotation symmetric Boolean functions with optimal algebraic immunity and high nonlinearity[J].Designs,Codes and Cryptography,2014,71(2):183-199. [18] Dillon J F.Elementary hadamard difference sets[C]//Proceedings of the Sixth Southeastern Conference on Combinatorics,Graph Theory,and Computing.1975:237-249. [19] Tu Z,Deng Y.A conjecture about binary strings and its applications on constructing Boolean functions with optimal algebraic immunity[J].Designs Codes & Cryptography,2011,60(1):1-14. [20] Massey J L.A spectral characterization of correlation-immune combining functions[J].IEEE Transactions on Information Theory,1988,34(3):569-571.2.5 函数W(x,y)的相关免疫性
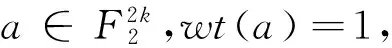

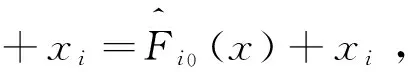
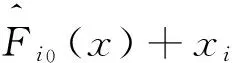
3 结 语
