星载复杂组件随机振动试验载荷设计方法改进

王跃宇，周志成，王 畅

（1.中国空间技术研究院 通信卫星事业部，北京 100094；2.北京联合大学 旅游学院，北京 100101）

0 引言

随着移动通信、微波遥感、在轨操作等系统技术的持续发展，对于宽口径、高增益的大型可展开天线和具有空间感知、机动和操作集成能力的空间机械臂的工程需求越来越多[1-5]。

大型可展开天线、空间机械臂等星（站）载复杂组件在开展结构设计时需要总体部门提供随机振动设计载荷。而目前已有的随机振动载荷估算方法在某些加载方向存在预示载荷过分偏离实际载荷的缺陷。随着以大型可展开天线为代表的星载复杂组件对于减轻重量、提高展开可靠性、实现结构与机构优化设计的需求日益增加，组件结构设计单位迫切希望总体能够给出既符合实际分布规律，又不过度偏离载荷幅值的载荷设计指标。

为解决组件需求与总体设计指标之间长期以来存在的矛盾，在深入研究国内外已有的随机振动载荷设计方法的基础上，本文提出了一种改进的设计方法。该方法既可以给出符合实际分布规律的设计载荷，又具有良好的预示精度，从而为载荷剪裁开拓出一条工程上实用而有效的技术途径。

1 已有的载荷设计方法

1.1 国外方法

对于复杂组件的随机振动试验载荷设计，国外航天器力学环境工程界已率先提出工程可用的载荷预示模型和设计方法，如欧洲ECSS-E-10-03A[6]标准中公布的方法，以下简称欧标法（European standard method,ESM）。

ESM实际上是基于2个假设：当组件质量不超过50 kg时，采用切向载荷和法向载荷相异的假设（切法异载假设）；当组件质量大于50 kg时，采用切向载荷和法向载荷相同的假设（各向同载假设）。

ESM 的主要思想是：在没有可靠的分析结果或其他型号类似组件随机振动试验数据可供参考的情况下，假设组件质量为m，按质量大小划分成为m≤50 kg和m＞50 kg两个区间，其分别对应的载荷预示模型如表1和表2所示。

表1 ESM载荷谱（m≤50 kg）Table 1 RV test levels of ESM (m≤50 kg)

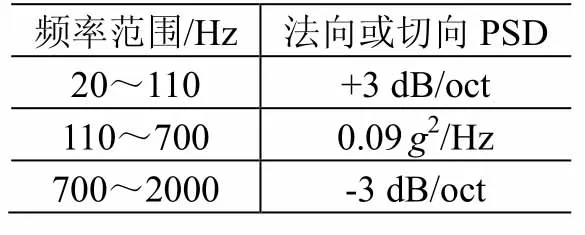
表2 ESM载荷谱（m＞50 kg）Table 2 RV test levels of ESM (m＞50 kg)

1.2 国内方法

尽管受到星载复杂组件数量十分有限、相关试验数据积累不足等不利条件的阻碍，我国仍坚持开展跟踪与探索性研究，借鉴国外经验，针对复杂组件的随机振动试验载荷设计提出了衰减因子法（attenuation factor method,AFM）[7]。

AFM 采用的载荷分布假设是各向同载假设。其主要思想是假设组件质量为m，按质量大小划分为m≤23 kg（甲）、23 kg＜m≤180 kg（乙）和m＞180 kg（丙）3个区间。这3个质量区间分别对应的载荷预示模型如表3所示。

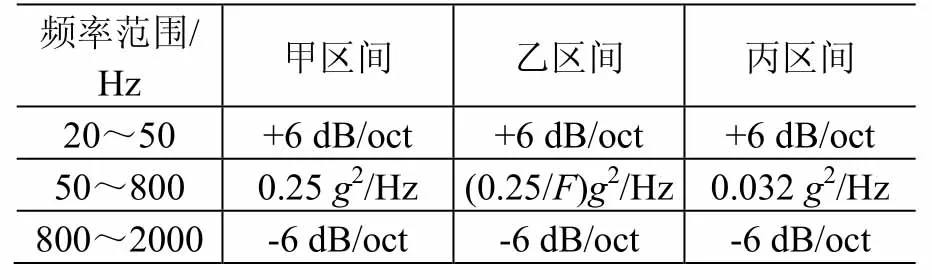
表3 AFM载荷谱Table 3 RV test levels of AFM

1.3 已有方法的局限性

已有设计方法的局限性表现在：1）在部分（例如ESM）或全部（例如AFM）质量区间采用了各向同载假设，忽略了载荷大小对加载方向的敏感性，违背了法向偏大、切向偏小的载荷分布规律；2）由ESM和AFM获得的载荷（总均方根加速度）预示值往往高于真实载荷，有时甚至高出 2倍以上，会导致复杂组件结构强度的冗余设计；3）ESM有时会给出小于实际载荷的预示结果，无法保证复杂组件载荷设计具有合理的安全裕度。

2 改进的载荷设计方法

为实现结构与机构的优化设计，天线研制部门迫切要求卫星总体设计部门在保证结构安全裕度的前提下，提高载荷预示精度、合理降低设计指标。为此，本文提出了一种改进的复杂组件随机振动载荷设计方法，简称方向质量法（loading direction and mass method,DMM）。其主要思想是：假定组件质量为m，按质量大小划分成DM01～DM05共5个质量区间，区间范围依次为m≤23 kg、23 kg＜m≤60 kg、60 kg＜m≤120 kg、120 kg＜m≤180 kg和m＞180 kg。这5个区间的随机振动试验载荷谱如表4～表8所示。

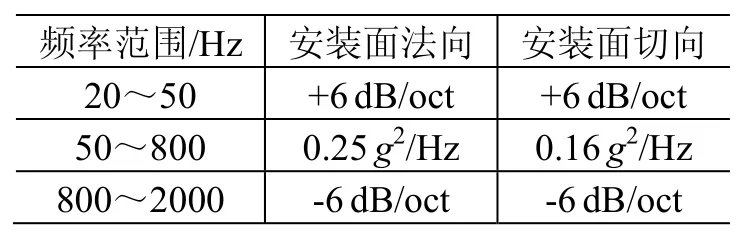
表4 DMM载荷谱（DM01区间）Table 4 RV test levels of DMM (Interval DM01)

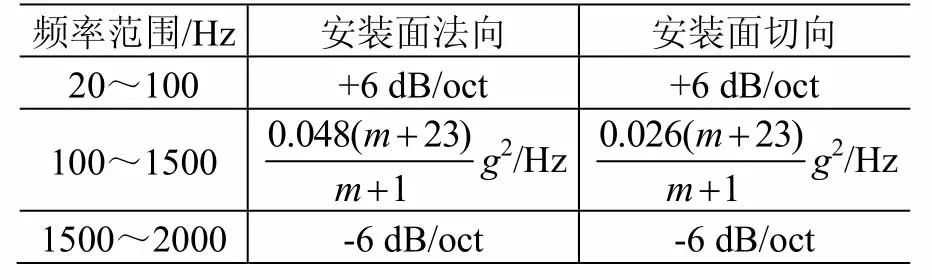
表5 DMM载荷谱（DM02区间）Table 5 RV test levels of DMM (Interval DM02)

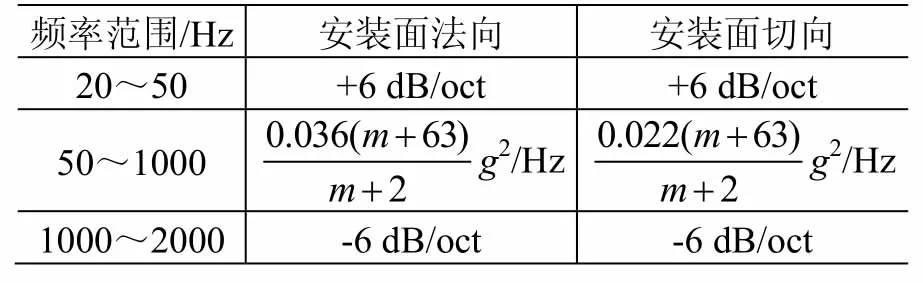
表6 DMM载荷谱（DM03区间）Table 6 RV test levels of DMM (Interval DM03)

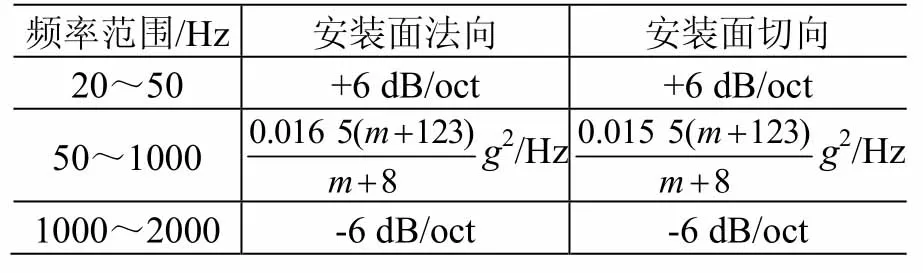
表7 DMM载荷谱（DM04区间）Table 7 RV test levels of DMM (Interval DM04)

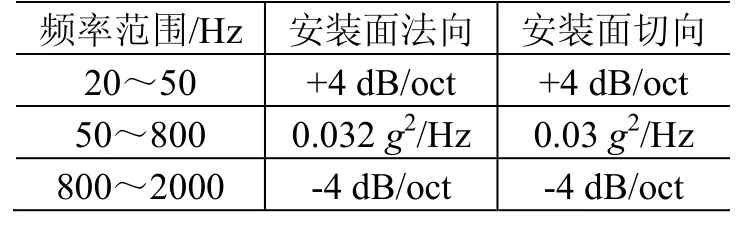
表8 DMM载荷谱（DM05区间）Table 8 RV test levels of DMM (Interval DM05)

DMM 载荷预示模型的建模步骤如下：1）以组件质量m为变量，将随机振动载荷谱假设为m的分式函数形式，其系数含有待定参数；2）引入载荷偏离度（load deviation,LD）的概念（定义见后），借助数学推导得到待定参数与卫星噪声试验实测结果之间的关系式；3）确定待定参数，从而获得既与组件质量相关，又反映加载实际规律的载荷谱。

下面以质量位于DM02区间，沿安装面法向加载的随机振动载荷为例，说明随机振动载荷预示模型的建模过程。

图1为随机振动典型谱，其中，f1～f2频段为上升谱，f2～f3频段为平直谱，f3～f4频段为下降谱。

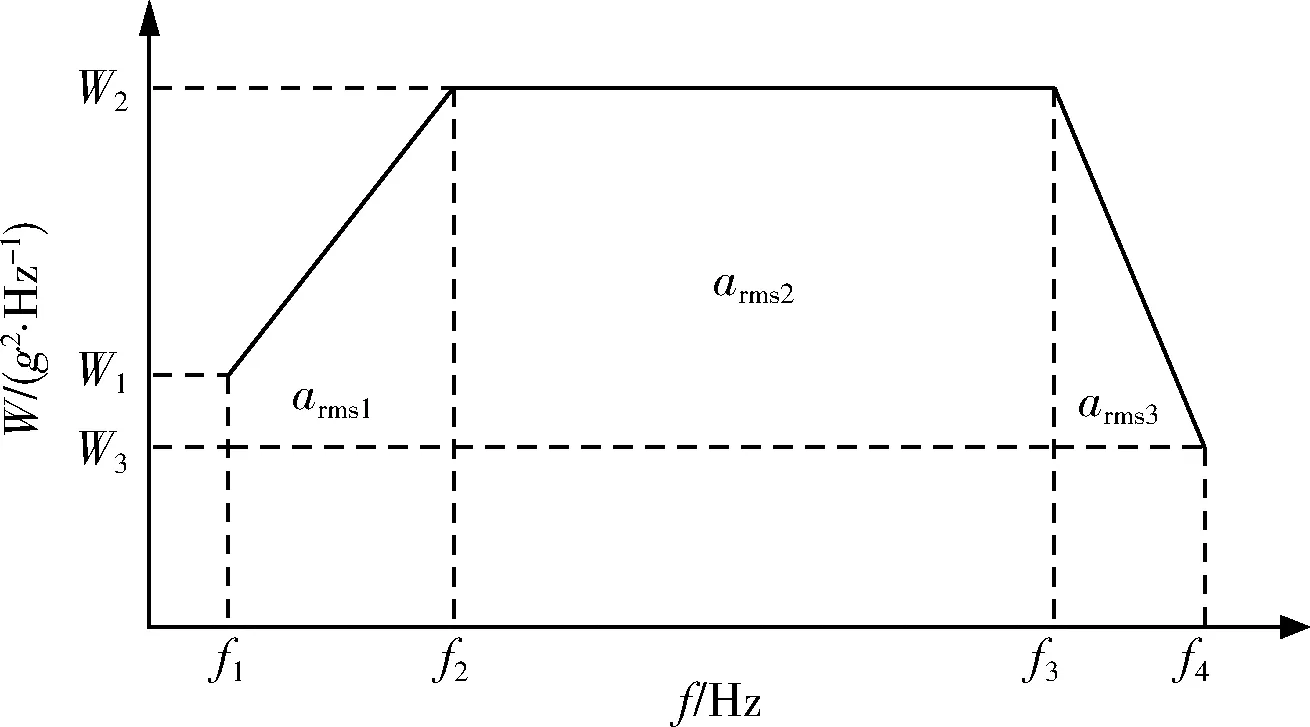
图1 随机振动典型谱Fig.1 Typical random vibration spectrum

上升谱的均方加速度为

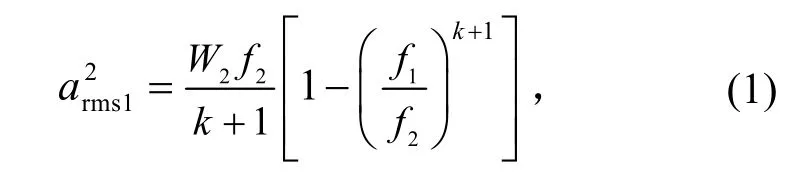
式中：f1和f2分别为上升谱的下、上限频率；W2为f2和f3处的谱密度；k为1/3倍频程分贝数。

平直谱的均方加速度为

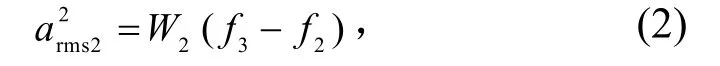
式中，f3为平直谱上限频率（或下降谱下限频率）。

下降谱的均方加速度为

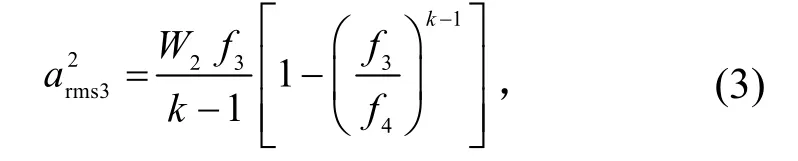
式中，f4为下降谱上限频率。

随机振动典型谱的均方根加速度[8]为

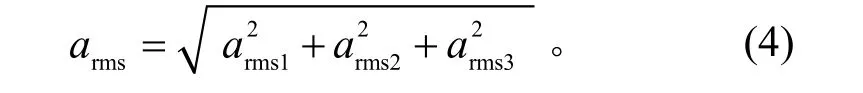
质量位于 DM02区间的天线组件，假设其安装面法向的随机振动载荷预示模型为

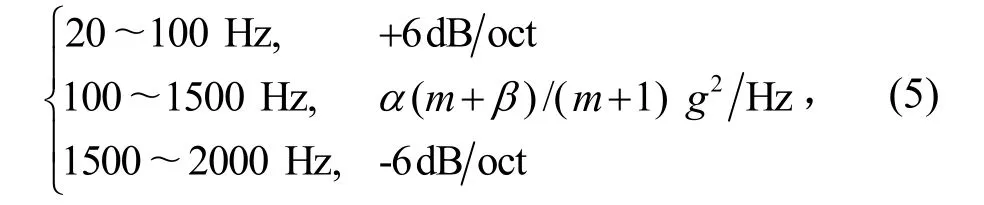
式中，α和β为待定参数。

将式(5)代入式(1)～式(3)，有：

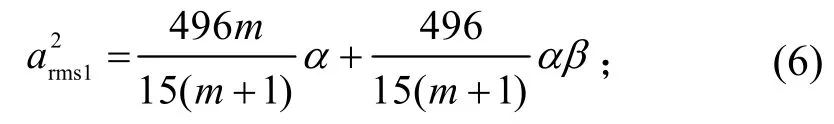
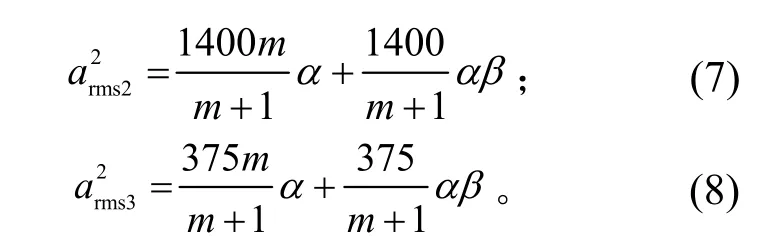
因此，总均方加速度为

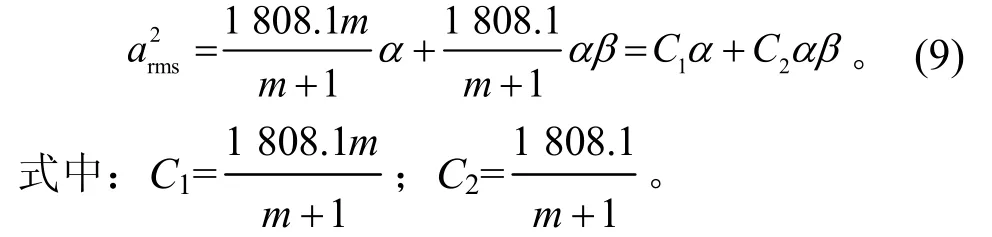
设at-rms为复杂天线组件在卫星噪声试验中连接界面处总均方根加速度的实测结果，arms为随机振动载荷预示模型给出的总均方根加速度，则预示结果的载荷偏离度为LD=[(arms-at-rms)/at-rms]×100%。设 LD=ε，且ε＞0，则有arms=(1+ε)at-rms。将该结果代入式(9)得到C1α+C2αβ=[(1+ε)at-rms]2。一般情况下，按照下限取整原则，β可以取质量区间下限附近的一个整数。这样，根据at-rms和ε的工程许用值，就可以确定α=[(1+ε)at-rms]2/(C1+C2β)。α和β值一旦确定，即可获得随机振动载荷的预示模型。

从内容上看，相对于ESM和AFM，DMM的主要创新体现在将23～180 kg的质量区间细分为3个区间，以卫星噪声试验实测数据为依据，分别沿复杂组件安装面的法向和切向提供全新的载荷设计模型。

3 三种方法的预示精度比较

本文选取了4个典型工程算例：环形天线反射器组件（组件 A）及其馈源组件（组件 B），伞状天线（组件C），管状天线（组件D）。各组件质量及其卫星噪声试验结果见表9。以LD为指标，利用DMM、ESM和AFM方法可以得到这4个组件的预示精度，详见表10～表13。

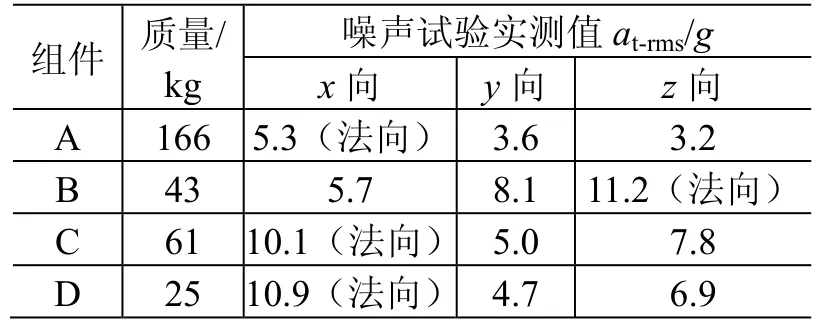
表9 组件质量及其噪声试验结果Table 9 Mass and acoustic test results of units

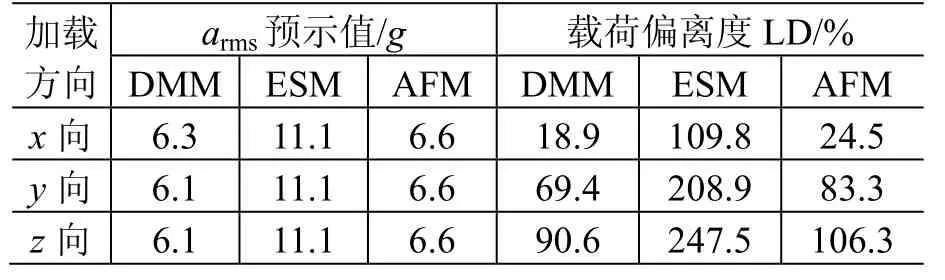
表10 组件A的预示结果及精度Table 10 Prediction results of unit A

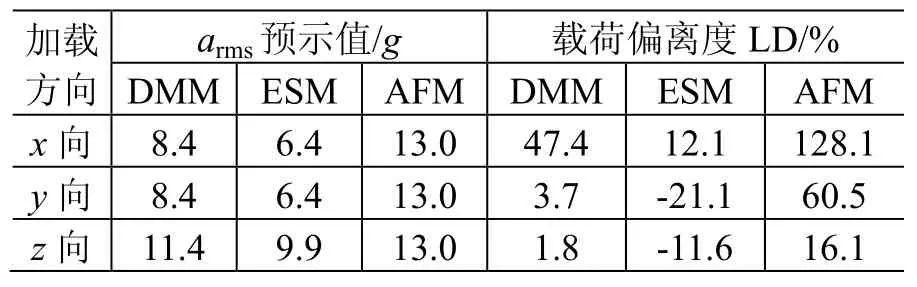
表11 组件B的预示结果及精度Table 11 Prediction results of unit B

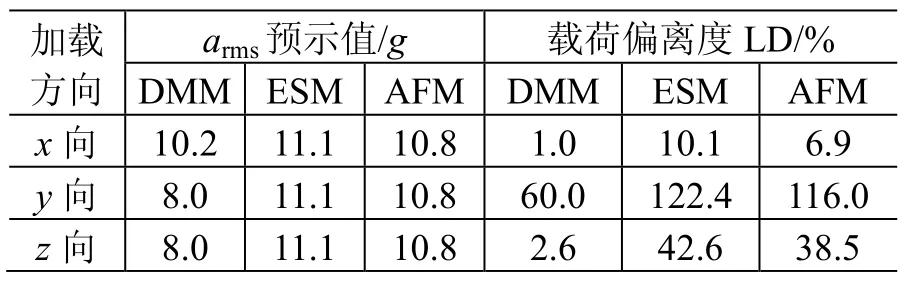
表12 组件C的预示结果及精度Table 12 Prediction results of unit C

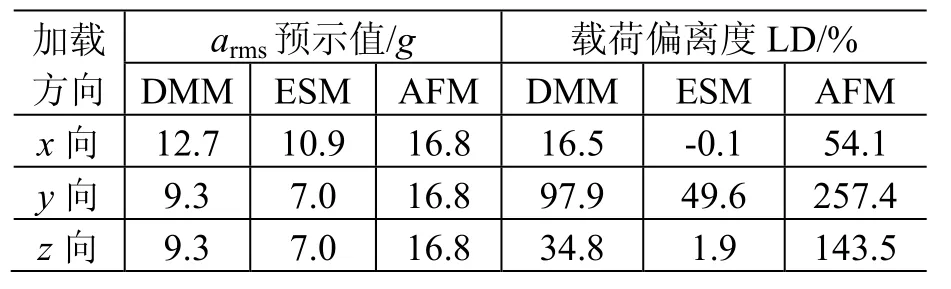
表13 组件D的预示结果及精度Table 13 Prediction results of unit D

观察表10～表13可知，组件B和组件D的ESM预示载荷偏离度LD出现负值，因此应将其相关数据从统计源中剔除。三种方法的平均误差参见表14。

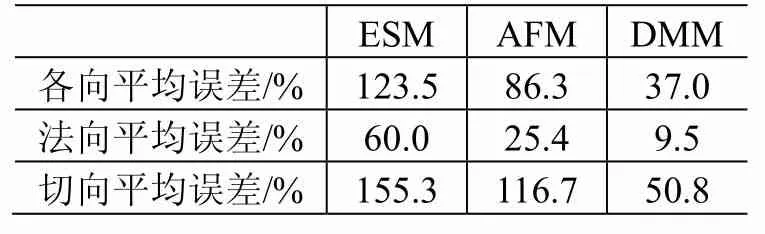
表14 三种方法的预示误差Table 14 Prediction errors of ESM,AFM and DMM

从表14可看出：和ESM相比，DMM的预示误差分别减少了70%（各向）、84.1%（法向）、67.3%（切向）；和AFM相比，DMM的预示误差分别减少了57.1%（各向）、62.5%（法向）、56.5%（切向）。可见，DMM的预示精度明显高于ESM和AFM，其预示结果最接近卫星噪声试验时组件安装部位的实测结果。

4 结束语

本文针对星载复杂组件随机振动试验载荷设计问题提出了一种改进的载荷预示方法（DMM），沿组件安装面不同加载方向分别提供了随机振动载荷预示模型，反映了振动载荷随加载方向变化的实际分布规律，顺应了国际环境工程技术的发展潮流。

DMM载荷预示模型的建模思路是以卫星噪声试验数据为基础，通过推导建立预示模型参数与实测物理参数之间的数学关联。从典型复杂组件随机振动载荷预示误差看，ESM和AFM的预示结果有可能与载荷设计要求发生抵触，这种潜在的风险无疑降低了其工程应用价值。DMM的预示精度明显优于ESM和AFM，给出的预示载荷最接近卫星噪声试验实测结果，可以替代后两者成为星载复杂组件中高频段力学环境设计的有力工具。

DMM解决了长期困扰总体载荷设计的一大技术难题，较好地满足了天线研制单位对随机振动载荷指标合理剪裁的技术需求，为今后各类星载复杂组件结构与机构优化设计工作的开展创造了有利条件。

（References）

[1]邬树楠,刘丽坤,汪锐,等.大型索网式可展开天线在轨高精度指向控制[J].宇航学报,2015,36(10):1140-1147 WU S N,LIU L K,WANG R,et al.On-orbit highaccuracy pointing control for large mesh deployable antenna[J].Journal of Astronautics,2015,36(10): 1140-1147

[2]DATASHVILI L,ENDLER S,WEI B,et al.Study of mechanical architectures of large deployable space antenna apertures: from design to test[J].CEAS Space Journal,2013,5(3): 169-184

[3]王辉,宋燕平,马小飞.星载大型柔性索网天线重力环境下的型面调试[J].中国空间科学技术,2016,36(4): 33-37 WANG H,SONG Y P,MA X F.Surface accuracy adjusting method of large flexible mesh spaceborne antenna on ground[J].Chinese Space Science and Technology,2016,36(4): 33-37

[4]张华振,马小飞,宋燕平,等.星载高精度环形网状天线设计方法[J].中国空间科学技术,2013,33(5): 1-6 ZHANG H Z,MA X F,SONG Y P,et al.Design method of high precision perimeter truss antenna on board[J].Chinese Space Science and Technology,2013,33(5): 1-6

[5]刘宏,蒋再男,刘业超.空间机械臂技术发展综述[J].载人航天,2015,21(5): 435-443 LIU H,JIANG Z N,LIU Y C.Review of space manipulator technology[J].Manned Spaceflight,2015,21(5): 435-443

[6]Space engineering: testing: ECSS-E-10-03A[S],2002

[7]航天器产品力学环境试验技术要求: Q/W 1226—2009[S],2009

[8]柯受全,金恂叔.卫星环境工程和模拟试验[M].北京: 宇航出版社,1996: 56-60