受限空间纳米线熔化过程的分子动力学模拟

房冉冉 张可 王维

摘要

碳纳米管内嵌纳米线复合材料可以综合二者的优异性能从而有更广阔的应用前景。本文利用分子动力学模拟手段探讨了碳纳米管以及受限空间对于Cu纳米线的熔化行为，发现受限空间对于Cu纳米线的熔点影响较小，应用碳纳米管内嵌纳米线这种复合材料时可以忽略碳纳米管的加入对纳米线熔点的影响。而碳纳米管的存在可明显增加内部纳米线的稳定性，其原子排布对内部纳米线的作用较大。另外，受限空间中纳米线的熔化轴向方向是从端部开始，而径向方向是从表面开始逐漸到芯部进行。

【关键词】分子动力学模拟 碳纳米管 纳米线

1 引言

自1991年lijima教授发现碳纳米管，一维纳米结构材料引起了世界各国学者的注意，掀起了研究热潮。一维纳米线由于形状上的各向异性，带来了更加复杂的物理性质和自组装行为，如果它们能被有序地、合理地组装成二维结构，将有利于研究尺寸和形状对它们的光学、磁性和电子特征的影响，并在制造实用的新型量子器件方面有广阔的应用前景。纳米线是直径处于纳米尺度10-100nm，长度可达微米量级的典型的一维线性纳米结构。纳米线因具有显著的量子效应而被称为“量子线”，具有纳米尺度下典型的表面效应、宏观量子隧道效应、小尺寸效应，从而表现出独特的电学、力学、光学和磁学等性能。近年来研究表明，纳米线对于未来电子、光电子和纳电子器件的发展将会带来巨大且深远的影响。目前，实验发现碳纳米管的中空结构可以内嵌纳米线获得一种新型的复合材料，从而为一维纳米结构材料的应用开辟了新的天地。本文旨在采用分子动力学模拟手段探讨受限空间中纳米线的熔化行为，为这一复合材料的应用奠定研究基础。

2 Cu纳米线在受限空间中熔化过程的模拟过程

整个建模过程采用Materials Studio软件，模拟过程采用LAMMPS软件包。具体模拟步骤如下：

（1）在Materials Studio软件中创建直径不同的Cu纳米线结构，利用Forcite模块进行能量最小化得到稳定的Cu纳米线结构。Cu纳米线的直径从20-40nm不等。

（2）采用Nose-Hoover控温和控压方法，轴向方向施加周期性边界条件，在径向方向采用非周期性边界条件，时间步长均设定为2.5 fs。

（3）采用EAM势函数来描述铜一铜相互作用，采用12-6 Lennard-Jones势函数来描述Cu与墙体之间以及碳纳米管中的相互作用。

（4）采用共轭梯度算法使能量最小化，得到300K下受限空间中Cu纳米线的能量最低构型。

（5）将纳米线以1K/ps的速度升温至2000K。

3 模拟结果分析讨论

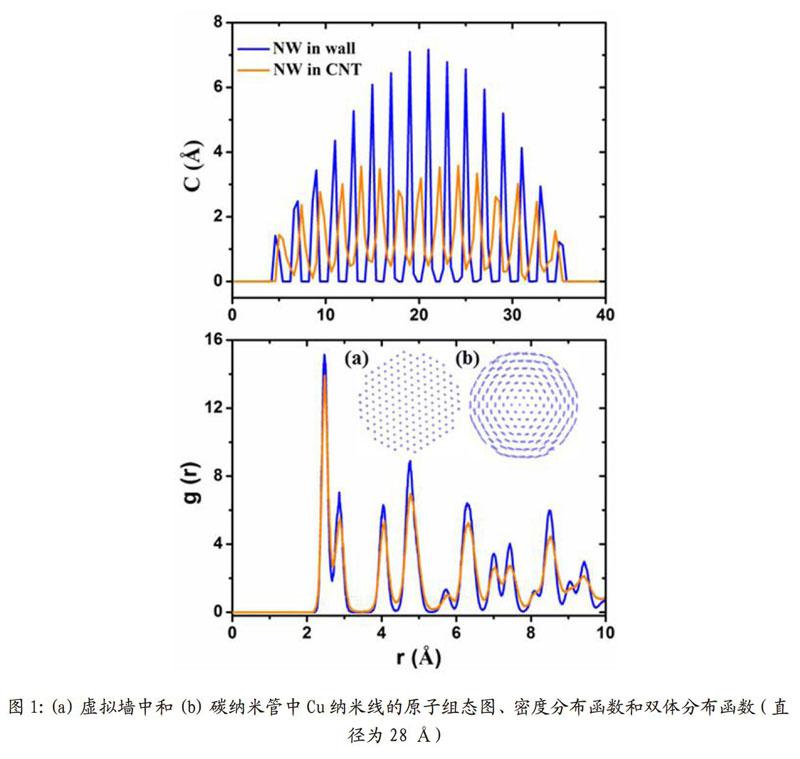
图1为稳定后300K时Cu纳米线在虚拟墙中和碳纳米管中的原子排布情况。如图所示，Cu纳米线在碳纳米管中和虚拟墙中的原子排布明显不同。碳纳米管中Cu纳米线不是规格的晶体排布形式，原先的原子面发生弯曲从而变为多层的圆形结构。通过（a）图中的密度分布函数可以看出，虚拟墙中的纳米线原子的密度分布与晶体十分相似，尖锐的各峰对应着各个原子面，且各峰之间的间距与面间距十分接近。而碳纳米管中纳米线各峰明显变钝变缓且高度平均趋于一致，这说明碳纳米管使纳米线的原子排布更加均匀。通过（b）图中的双体分布函数可以看出，碳纳米管中Cu纳米线虽然变为了多层的圆柱结构，但是其仍为晶体结构。

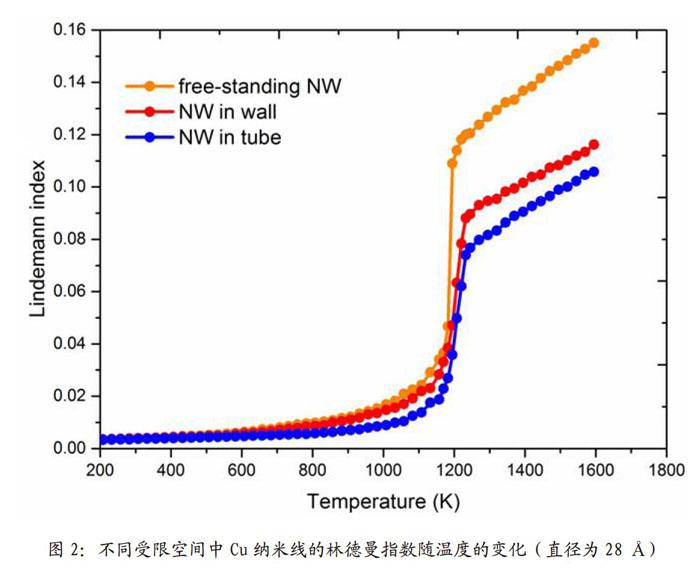
图2对比了直径为28A的Cu纳米线在虚拟墙中和碳纳米管中的林德曼指数曲线。利用林德曼指数的变化趋势可以看出原子的运动，以及熔点的确定。如图所示，首先，碳纳米管和虚拟墙中纳米线的熔点差别较小，即这两种受限空间对于纳米线的熔点影响不大。从图线中可以看出，自由状态的纳米线熔点大约在1183K。其次，碳纳米管中Cu纳米线原子的林德曼指数最低，说明碳纳米管对于碳纳米管对于纳米线原子运动的束缚更强。碳纳米管的存在可增加内部纳米线的结构稳定性。由于之前设定的Cu与两种受限空间的相互作用势函数参数相同，而不同之处在于碳纳米管不仅具有尺寸限制，其管壁上碳原子的排布是虚拟墙不具备的。因此碳纳米管壁碳原子的排布对于内部纳米线的熔化影响较大。

为了进一步揭示纳米线的熔化行为，我们在图3中给出了特定温度下纳米线的原子组态图。首先，从图3中可以看出，300K时，纳米线的结构与晶体结构相似。径向分布函数g（r）可以作为原子排布形式的辅助分析手段，我们在图4中给出了特定温度下纳米线原子的径向分布函数。可以看出，300K时，纳米线原子的径向分布函数呈现明显的各峰，第一峰的横坐标正好对应Cu的原子间距，说明此时Cu纳米线呈现晶体结构。随着温度的增加，当温度到达900K时，纳米线原子组态发生了变化，轴向两端已经放弃了先前规则的晶体排布，而纳米线的芯部还可见规则的晶体结构排布形式。结合该温度下的径向分布函数g（r）可知，各峰仍然较为明显，说明纳米线总体认为晶体结构。当温度到达1000K时，纳米线放弃先前规则的晶体排布的原子个数增加，芯部保持晶体结构的区域减少，说明熔化在进一步进行。该温度下的径向分布函数中仍可看出明显的各峰，且峰的个数与900K时一致。当温度到达1183K时，这也是从林德曼指数曲线中确定的纳米线的熔点，从径向分布函数中可看出发生了明显变化，呈现液态分布，这与林德曼指数曲线确定的体系的状态是一致的。当温度到达1400K时，呈现完全的液态分布状态。

为了进一步揭示纳米线的熔化行为，我们还计算了纳米线原子的林德曼指数来揭示其熔化的过程。林德曼指数是近年来研究体系熔化行为的重要物理参量之一，其原理是通过对原子的位移做数学统计来确定原子的状态。研究表明，整个体系的林德曼指数的突变可以定义为体系的熔点。当体系处于固态时，体系原子均在平衡位置附近做微小的位移，从而其林德曼指数较小;而在熔化时，体系原子的振动加剧，林德曼指数会突然增加至3倍以上。因此，林德曼指数突然增加所对应的温度通常可以作为体系熔点的确定手段。在这里，我们把林德曼指数高于临界值的原子称之为林德曼原子，认为这些原子己处于熔化状态，以此在原子组态图中做出林德曼原子的分布情况。我们在图3的原子组态图中用不同颜色进行标记，蓝色为非林德曼原子，白色为林德曼原子。从图中可以清晰的看出，在300K时，所有的原子都处于林德曼原子状态。随着温度的增加，当温度到达900K时，轴向端部以及径向表面的部分原子成为林德曼原子，说明此时熔化慢慢开始，熔化从轴向方向两端开始的，而径向方向是从表面到芯部进行。 1000K时，林德曼原子的比例继续增加，此时可以看出，轴向端部的绝大部分原子都已经成为林德曼原子，而非林德曼原子集中在芯部位置。1183K时，并不是所有的原子都处于液态成为林德曼原子，纳米线的芯部原子其实还处于晶体状态。由此可知，熔点并不是所有原子都熔化，而是熔化的原子达到一定比例。1400K时，所有的纳米线原子都成为了林德曼原子，纳米线彻底熔化。

4 結论

本文利用分子动力学模拟手段（主要利用Materias Studio以及LAMMPS软件包）探讨了受限空间中Cu纳米线的熔化行为，并对模拟结果进行分析讨论，结论如下：

（1）受限空间对于Cu纳米线的熔点影响较小，应用碳纳米管内嵌纳米线这种复合材料时可以忽略碳纳米管的加入对纳米线熔点的影响。

（2）碳纳米管对于碳纳米管对于纳米线原子运动的束缚更强，碳纳米管的存在可增加内部纳米线的结构稳定性。碳纳米管上原子的排布对于内部纳米线的熔化影响较大。

（3）受限空间并没有改变内部纳米线的熔化行为，受限空间中纳米线的熔化轴向方向是从端部开始，径向方向是从表面开始到芯部进行。

参考文献

[1]Iijima S.Helical microtubulesof graphitic carbon[J].Nature，354（6348），56-58（1991）.

[2]X.W.Zhou，H.N.G.Wadley，R.A.Johnson，D.J.Larson，N.A.Tabat，C.A.K.Petford-Long，G.D.W.Smith，P.H.Clifton，R.L.Martens，T.F.Kelly.Atomicscale structure of sputteredmetal multilayers[J].ActaMater.49，4005-4015（2001）.

[3]S.P.Huang，D.S.Mainardi，P.B.Balbuena，Structure and dynamicsof graphite-supported bimetallicnanoclusters，Surf.Sci.545，163-179（2003）.

[4]Fang R R，He Y Z，Zhang K，Li H.Melting Behavior of AluminumNanowires in Carbon Nanotubes[J].The Journal of Physical Chemistry C.2014，118（14）：7622-7629.

[5]Stillinger F，Weber T.Lindemannmelting criterion and the Gaussiancore model[J].Physical ReviewB.1980，22（08）：3790.

[6]Hui L，Pederiva F，Wang B，Wang J，Wang G.How does the nickel nanowiremelt？[J].Applied Physics Letters.2005，86（01）：011913.

[7]Yan J A，Yang L，Chou M Y.Size andorientation dependence in theelectronic properties of siliconnanowires[J].Physical ReviewB.2007，76（11）：115319.

[8]Qin X F，Deng C H，Liu Y，MengX J，Zhang J Q，Wang F，et al.Magnetization Reversal of HighAspect Ratio Iron Nanowires Grownby Electrodeposition[J].IeeeTransactions on Magnetics.2012，48（11）：3136-3139.

[9]Davidchack R L，Laird B B.Directcalculation of the crystal-meltinterfacial free energies forcontinuous potentials：Applicationto the Lennard-Jones system[J].Journal of Chemical Physics.2003，118（16）：7651-7657.

[10]Zhang Y，Wen Y H，Zheng J C，Zhu Z Z.Energetic and structural evolution ofgold nanowire under heating process：Amolecular dynamics study[J].PhysicsLetters A.2009，373（38）：3454-3458.