基于PNGV模型储能锂电池参数辨识及SOC估算研究

甘屹+李杨+姚俊

摘 要： 锂电池因具有比能量高、循环寿命长、对环境无污染等优点，在储能系统中已逐渐得到应用.准确估算锂电池的荷电状态（SOC）可防止电池过充、过放，保障电池安全、充分地使用.为了精确估算储能锂电池SOC，基于PNGV（partnership for a new generation of vehicles）电池等效模型，利用递推最小二乘法（RLS）对模型参数进行在线辨识和实时修正，增强了系统的适应性.结合安时法、开路电压法和PNGV模型，提出了一种实时在线修正SOC算法.根据实验数据，建立了仿真模型，以验算模型和SOC估算算法的精度.仿真结果表明，PNGV模型能真实地模拟电池特性，且能有效地提高SOC估算精度，适合长时间在线估算储能锂电池的SOC.

关键词： 锂电池； PNGV模型； 荷电状态； 递推最小二乘法

中图分类号： TM 912 文献标志码： A

Abstract： Lithiumion batteries have been gradually applied toenergy storage system with the advantages of high energy density，long cycle life，no pollution to environment and so on.Accurate stateofcharge（SOC）estimation of lithiumion battery can avoid the overcharge or overdischarge，make full use of the battery and guarantee the battery safety.In order to accurately estimate SOC for energy storage lithiumion battery，recursive least squares method（RLS） was adopted for online identification and realtime modification of the model parameters to enhance the system adaptability according to the equivalent battery model of partnership for a new generation vehicles（PNGV）.Combined with Amperehour method，open circuit voltage method and PNGV model，an online modified SOC algorithm was proposed.The simulation model was established using the experimental data to verify the accuracy of the model and the SOC estimation.The simulation results showed that the algorithm could effectively improve the accuracy of SOC estimation，and was suitable foronline estimation of SOC for energy storage lithiumion battery for a long time.

Keywords： lithiumion battery； PNGV model； SOC； RLS

新能源的取之不尽和无污染等优点使其成为未来发电技术的发展方向[1].储能电池在各种新能源储能技术中发展最为成熟，其发展催生了新能源储能电池技术和产业.锂电池具有比能量高、循环寿命长、对环境无污染等优点，国内外越来越多的储能电站选择锂电池作为储能电池[2].但是，锂电池对电压、温度和电流的要求极为严格，使用过程中稍有不慎就可能导致电池损伤，甚至引发安全事故.因此，电池管理系统（battery management system，BMS）具备的功能有：数据采集、电池荷电状态（state of charge，SOC）估算、均衡控制、熱量约束、数据通讯和使用安全等[3].SOC是指电池的剩余电量，是BMS控制策略的重要依据.

目前，常见的SOC估算算法有开路电压法、安时法、神经网络法、扩展卡尔曼滤波（EKF）法等[4].安时法、开路电压法或结合两者所衍生出的是常见的SOC估算算法[5].这些传统的算法计算简单，易于实现，但精度低，易产生累计误差.

基于锂电池等效电路模型的智能算法具有较高的精度，但计算复杂，估算精度依赖于电池模型的精确性[6].影响电池模型精确性的主要原因是其参数在电池使用中会随着温度、充放电电流、老化程度等因素变化，因此需要对模型参数实时在线辨识和修正.递推最小二乘法（recursive least square，RLS）广泛应用于动态模型的参数在线辨识[7]，辨识参数越多，计算量越大.PNGV（partnership for a new generation of vehicles）模型是根据美国新一代汽车合作计划，在2001年《PNGV电池实验手册》中提出的等效电路模型，并沿用为2003年《FreedomCAR电池实验手册》中的标准电池性能模型[8].

为了考察电池使用过程中动态变化的参数，本文以标称为20 Ah的储能锂电池作为研究对象，建立锂电池的PNGV等效电路模型，优化模型的参数辨识，结合安时法、开路电压法等方法，提出一种实时在线辨识和修正SOC的算法，并通过实验进行验证.

1 锂电池等效电路模型endprint

目前常见的等效电路模型有内阻模型、一阶RC模型、戴维南模型、PNGV电池等效模型和通用性的非线性（general nonlinear，GNL）模型[9].为了获取更高的模拟精度，每一种等效电路模型均是在其前一种模型的基础上，通过相应的方法形成.其中，PNGV电池等效模型属于非线性低阶模型，比简单的内阻模型、一阶RC模型、戴维南模型精度高.而GNL模型计算太复杂，不适合锂电池SOC估算的实验仿真和实际应用.综合考虑模型的实用性和精确度，本文选择PNGV电池等效模型作为电池外部特性仿真的对象.

1.1 PNGV等效电路模型

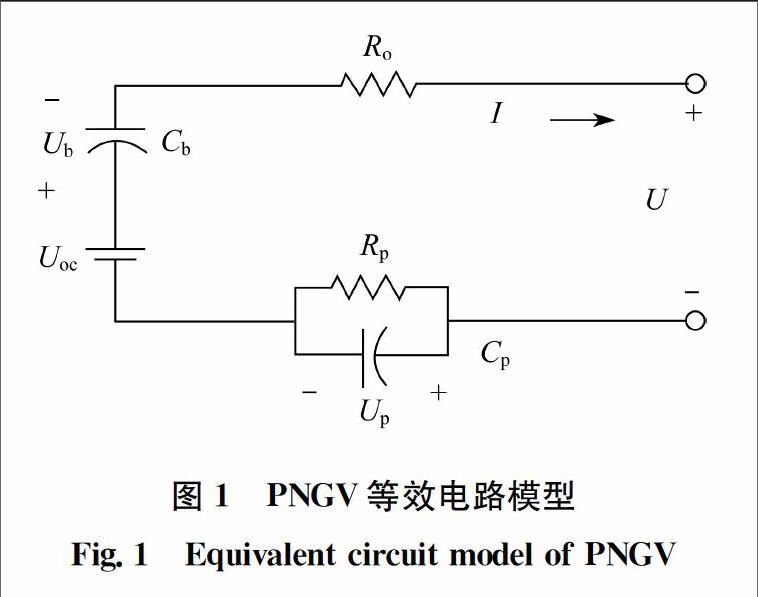
根据文献[10]，PNGV 等效电路模型的电路结构如图1所示.

2.2 算法验证及分析

为了验证上述方法的准确性，同时考虑到储能电池的电流较为平稳，本文在常温下对标称为20 Ah储能锂电池进行1 C脉冲电流放电实验，然后在放电结束后静置2 h，测量其开路电压，根据开路电压与SOC的关系得到的SOC为34.8%.

图7为利用Matlab软件中Simulink模块进行SOC估算的仿真图.图8为20 Ah储能锂电池分别在1 C脉冲电流放电下采用安时法和基于模型的修正算法估算的SOC随时间的变化.表1分别给出了利用安时法、基于PNGV模型的修正法，并在充分静置后开路电压估算得到的SOC对比结果.

仿真结果表明，当恒流放电时，起始阶段时利用安时法与基于PGNV模型的修正法估算得到的SOC结果相近.但是随着系统的运行，两者逐渐出现了微小的偏离，利用基于PNGV模型的修正法得到的SOC精度更高.这是因为电流采样频率和精度等因素会引起一定误差，长期利用安时法估算SOC会引起累计误差.利用基于PNGV模型的修正法可以实时修正安时法的误差，消除安时法引起的累计误差，适合长时间在线估算SOC.因此，该算法对电流平稳变化的储能系统是适用的.

3 结 论

本文分析了PNGV等效电池模型的结构，利用RLS算法，实时辨识模型参数，可以消除温度、充放电倍率和电池老化等因素对模型的影响，有效提高电池模型的精度.本文提出的基于PNGV模型的修正法对SOC进行在线估算，充分利用安时法和开路电压的优点，同时不断修正安时法的累计误差，以消除电池自放电的影响.实验结果表

明，与安时法相比，该算法误差更小，精度更高，适合长时间在线估算SOC.该算法与其他智能算法相比，在确保SOC估算精度的同时，可以降低计算量.

参考文献：

[1] 童广浙.磷酸铁锂储能电池管理系统设计[D].南宁：广西大学，2013.

[2] 范宝骥.我国新能源储能電池产业技术经济分析[D].长春：吉林大学，2010.

[3] 甘屹，陈成，曾乐才.5 kW锂电池模组BMS的研究与开发[J].能源研究与信息，2015，31（2）：114-118.

[4] 毛群辉，滕召胜，方亮，等.基于UKF的电动汽车锂电池SOC估计方法[J].测控技术，2010，29（3）：89-91.

[5] 华周发，李静.电动汽车动力电池SOC估算方法综述[J].电源技术，2013，37（9）：1686-1689.

[6] 李琳辉，王蒙蒙，周雅夫，等.电动汽车用动力电池SOC估算方法概述[J].汽车电器，2013（12）：12-15.

[7] VERBRUGGE M.Adaptive，multiparameter battery state estimator with optimized timeweighting factors[J].Journal of Applied Electrochemistry，2007，37（5）：605-616.

[8] 贾玉健，解大，顾羽洁，等.电动汽车电池等效电路模型的分类和特点[J].电力与能源，2011，32（6）：516-521.

[9] 张利，张庆，常成，等.用于电动汽车SOC估计的等效电路模型研究[J].电子测量与仪器学报，2014，28（10）：1161-1168.

[10] JOHNSON V H.Battery performance models in ADVISOR[J].Journal of Power Sources，2002，110（2）：321-329.

[11] ENGELY，MANNORS，MEIR R.The kernel recursive leastsquares algorithm[J].IEEE Transactions on Signal Processing，2004，52（8）：2275-2285.endprint