组坯胶合木梁受弯性能有限元分析★
2018-02-26王彦军
郭 楠 王彦军
(东北林业大学土木工程学院,黑龙江 哈尔滨 150040)
0 引言
现代木结构中胶合木梁被广泛应用,对胶合木梁受弯性能的要求也越来越高。组坯方式对胶合木梁的性能有重要影响,研究层板对胶合木梁性能的影响对提高胶合木梁的性能以及提高板材的利用率有重要意义。传统的胶合木梁是直接将层板胶合在一起,并没有考虑各层层板的性能,组坯方式对整体的性能的影响也没有考虑,继而木梁的强度就没有得到充分的利用,造成材料浪费[1-4]。因此本文通过ABAQUS分析软件进行建模,研究受压次外层、受拉最外层以及相同弹模的板数量相同时,不同等级的板的不同组坯方式对胶合木梁的受力性能的影响,为其在实际工程中的应用提供理论基础。
1 模型基本情况
1.1 基本信息
胶合木梁的跨度为3 750 mm,截面尺寸为180×200,层板的厚度为33 mm,不同等级的层板根据不同的组坯方式布置,其试验装置及位移计布置如图1所示。

胶合木梁试验与有限元模拟的荷载—挠度关系曲线的对比关系如图2所示。

1.2 模型分组
试验模拟的是规范中21等级的胶合木梁,共计7组梁,编号为An,其中n为序号1~7,组坯情况及编号如图3所示。

2 有限元建模
2.1 概况
根据试验情况,梁破坏不是由于层板间胶层的破坏或是开裂,所以认为模型层板间不发生滑移,故用绑定约束。针对本试验特点,有限元根据5个层板的本构关系分层建立梁模型。设置模型的网格大小为20 mm。部件均采用八节点热耦合六面体单元,三项线性位移,三项线性温度单元(C3D8T)。
2.2 本构关系
本试验木材的本构关系是根据木棱柱体抗压试验得到的。本模型根据组坯方式的不同,逐层输入本构关系,不同等级层板的本构关系如图4所示。

2.3 约束及荷载
荷载是逐级施加的,根据试验加载制度,每分析步设置10 kN的力。试验梁采用两端铰接约束,左端限制X,Y,Z轴的移动和绕X,Y轴的转动;右端限制Y,Z轴的移动和绕X,Y的转动。木梁左端的自由度设置为U1=U2=U3=UR1=UR2=UR3=0;木梁右端的自由度设置为U2=U3=UR1=UR2=0。
3 结果及分析
3.1 受拉第二层层板影响
将受拉次外层板从Me10提高到Me12,研究受拉第二层层板对胶合木梁整体性能的影响,其变形图,云图和挠度图分别如图5~图7所示。

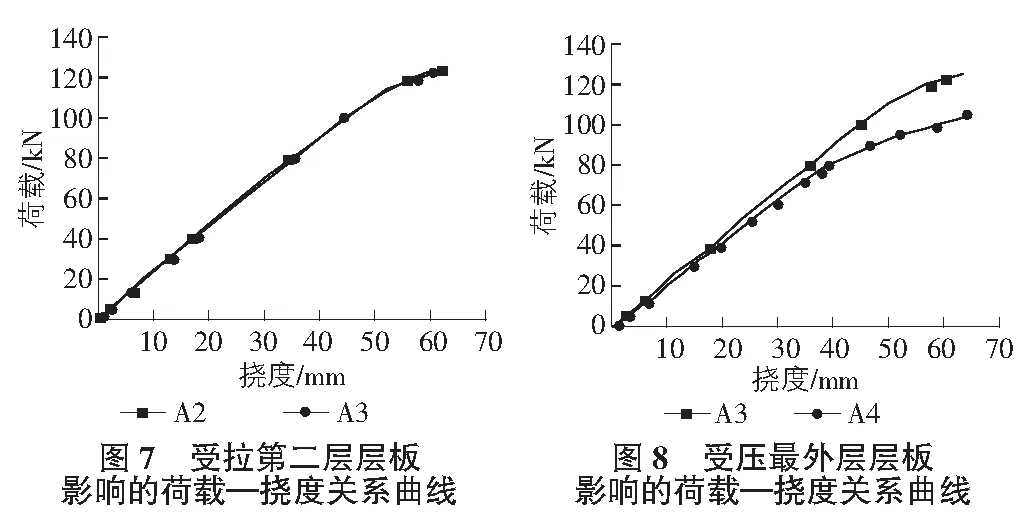
受拉次外层板从Me10提高到Me12时,对比分析可得,受拉第二层层板对梁的受弯性能几乎没有影响。
3.2 受压最外层层板影响
将受压最外层层板的弹模等级从Me10提高到Me12,研究受压最外层层板对胶合木梁整体性能的影响,其荷载—位移曲线如图8所示。
受压最外层板从Me10提高到Me12时,对比分析可得,受压最外层板对梁的受弯强度有影响,抗弯承载力提高19.04%。
3.3 相同弹模层板数目相同的条件下,不同组坯方式对梁的受弯强度的影响
选取与规范中异等21等级相同等级数量的板材,将等级高的板材分别置于受拉与受压位置,研究相同弹模层板数目相同的条件下,不同组坯方式对梁的受弯强度的影响,其荷载—挠度曲线如图9所示。

对比分析可得,弹模大的板置于最外层较置于受拉层最大承载力提高38.75%,弹模大的板材置于外层时,更能发挥自身的强度,更能提高梁的整体性能。
3.4 最强弹模的板和最弱弹模的板的受力位置不同对梁的受弯强度的影响
研究最强弹模的板和最弱弹模的板的受力位置不同对梁的受弯强度的影响,如图10所示。
对比分析可得,异等21等级中,将最高等级的层板置于受拉位置较置于受压位置最大承载力提高24.5%。
4 结语
受拉最外层对梁的受弯性能影响较大,应把高等级的板首先置于受拉最外层,受压最外层次之,以提高梁的整体受弯性能,对提高材料的利用率有重要意义。
[1] Kjell Sollo,Erik Aasheim,Robert H.Falk. The strength of Norwegian glued laminated beams[C].Proceedings,25th meeting of international council for building structures;1992 august 24-27;Ahus Sweden.Ahus,Sweden:CIB-W18;1992.8p.
[2] Roland Hernandez,Russel C.Moody. Analysis of glulam timber beams with mechanically graded (E-rated) outer laminations[C].Perceedings of the international wood engineering conference;1996 October 28-31;New Orleans, LA Baton Rouge,LA: Louisiana State University.Vol 1:144-150.
[3] M.Frese, H.J.Bla. Beech glulam strength classes[C].International council for research and innovation in building and construction:CIB-W18/38-6-2.
[4] 张文福,王 戈.组坯结构对竹束单层压板物理力学性能的影响[J].中南林业科技大学学报,2012(32):47.
[5] 左宏亮,杨颖伟,郭 楠,等.预应力胶合木张弦梁受弯性能有限元分析[J].辽宁工程技术大学学报(自然科学版),2015(3):121-122.
[6] 张济梅,潘景龙.ANSYS分析张弦木梁的变形性能[J].低温建筑技术,2008(4):70-71.
[7] Nima Khorsandnia, Hamid Valipour, Stephen Foster,et al.A force-based framefinite element formulation for analysis of two-and three-layered composite beams with material non-linearity[J].International Journal of Non-Linear Mechanics,2014(62):12-22.
