基于电化学机理模型的锂离子电池参数辨识及SOC 估计
2018-02-25邓忠伟李冬冬蔡亦山羌嘉曦
邓 昊,杨 林,邓忠伟,李冬冬,杨 洋,蔡亦山,羌嘉曦
(1.上海交通大学 机械与动力工程学院,上海 200240;2.上海凌翼动力科技有限公司,上海 200240)
电动汽车已成为国内外汽车科技发展的重点。如何准确估计SOC(电池电量),是电动汽车发展中亟待解决的关键问题。现有的SOC 估计方法,除基于完全依赖实验数据的数据模型外,主要基于等效电路模型(ECM),其具有模型简单、计算方便的优点[1-2]。但数据模型的实验工作量大、难于全覆盖电池在电动汽车等应用的全部工况,等效电路模型亦属于经验模型,不能体现电池实际的物理参数,因而无法描述电池内部的电化学行为与物理特性。相比而言,电化学机理模型(如P2D,pseudo-two-dimensional)[3]是根据电池内部机理建立电化学动力和传输方程组,因此,可以更准确地描述电池的运行状态、健康状态,提高了电池SOC 估计的准确性。但P2D 模型的控制方程[4]之间的耦合程度高、计算量大。需要对P2D 模型进行合理简化,才能用于电池管理系统(BMS)等实时应用中。而简化后的SP2D(simple pseudo-twodimensional)模型仍然参数过多[5-6],且各参数对电池输出电压的敏感度不同,难以准确辨识全部参数,因而依然难以解决SOC 在线估计的问题。
本文将在简化P2D 模型(SP2D)的基础上,提出基于模型参数可辨识性分析的最优辨识参数组及参数辨识方法,解决参数辨识问题;进而研究基于SP2D 的SOC 自适应卡尔曼滤波(adaptive extended Kalman filter,AEKF)估计算法,实现对SOC 的准确在线估计;并通过对某款车用磷酸铁锂电池(容量为94 AH,具体参数由电池生产企业提供,如表1 所示)的实验,对比基于ECM 和SP2D 两种模型的SOC 估计方法,验证本文方法的有效性。θ 为电荷比。

表1 实验电池参数Tab.1 Parameters of the experimental battery
1 锂离子电池电化学机理模型SP2D
电池P2D 模型由4 个偏微分方程和1 个代数方程组成[7]。分析表明,简化P2D 模型中液相浓度、固相表面浓度和反应电流的计算,是简化P2D 模型的关键。为此,在SP2D 模型中分别利用了多项式近似的方法来计算这3 项的分布(表2)。图1 是模型的坐标基准。Lp为电池正极部分的长度;Ls为隔膜部分的长度。在表2 中,液相浓度ce由式(1)表示,通过对式(2)进行离散化,迭代求解液相浓度积分Qe,n[6],得到每一个时刻液相浓度 ce的 分布。反应电流 jf用三阶多项式(式(3))近似求得,通过取式(4)在y=0,, Ln时[5]建立的3 个方程迭代求解。其中,y 为电池各部分相应的位置坐标,Ln为电池负极部分的长度, κeff为有效液相电导率,σeff为有效固相电导率。考虑到电极的多孔性,取Bruggeman 系数得 κeff=κε1e.5,σeff=σε1s.5。固相表面浓度采用PP 方法(曲线近似方法)[7],将粒子固相浓度 cs以多项式(6)近似求得,通过表面浓度 cs,sur,平均浓度 cs以 及体积平均浓度流 q 建立式(7)来求解得到。由于这3 个参数只和反应电流 jf有关,因此,代入 jf即可以得到固相表面浓度cs,sur的分布。表2 中的公式只给出了负极部分这3 个分布的求解方法,正极与隔膜部分的求解方法与此类似。 ϕs(y),ϕe(y),U(y)分别为固相电势、液相电势、平衡电势,T 为绝对温度,F 为法拉第常数,De,n,eff为有效液相扩散系数,R 为粒子半径,I 为电流,I0为反应电流密度。

图1 模型坐标基准Fig.1 Model coordinate baseline

表2 电化学机理SP2D 模型方程Tab.2 Equations of the electrochemical SP2D model
电池SP2D 模型的电压输出由式(8)表示[6],式中,第1 部分为平衡电势引起的压降,第2 部分为过电势引起的压降,第3 部分为电解液电势引起的压降,第4 部分为SEI 膜的反应电流(固体电解质界面膜)引起的压降。其中:由 jf分布可以得到式(8)的第2,4 部分;由固相表面浓度 cs,sur代入式(5),可以得到方程的第1 部分;利用 jf和ce可求得方程的第3 部分。
基于该简化模型,可以解除P2D 控制方程间的高度耦合,减少模型计算量。在仿真步长为1 s,工况采用美国联邦城市标准(Federal Urban Driving Schedule,FUDS),循环时间7 500 s 下,P2D 模 型 计 算 时 间 为357 s,而SP2D 只 需 要4.7 s,计算时间大大缩短,仅为P2D 模型的1.3%。如按单步计算,则SP2D 每步计算仅需0.63 ms,模型本身可以满足BMS(电池管理系统)实时应用的要求。
2 模型参数敏感度分析及辨识
2.1 Fisher 信息矩阵和准则数RDE
参数辨识的准确性直接影响模型的精度。由于SP2D 模型中的参数有30 多个(表1),除去容易辨识的参数后也多达17 个(表3 中参数组A-A,记为Par17)。Rint为电池的内阻。研究表明,这些参数对电池电压的敏感度差异较大,难以同时辨识所有参数。因此,本文使用Fisher 信息矩阵进行参数可辨识性分析,并对分析出的最优辨识参数组进行辨识,解决模型参数辨识的准确性问题。
假定电池模型输出电压 V 和模型参数的关系符合正态分布,可得式(9)。其中,Ψ ,Z 为正态分布的期望值和方差, Par为模型参数组向量,t 为时间,概率密度

进一步得参数组向量 Par下 输出 V的概率,即联合概率密度P(式(10))。为求解方便,将P 写成对数形式,从而将连乘和指数消除。

表3 参数敏感度排序表Tab.3 Parameters sensitivity list
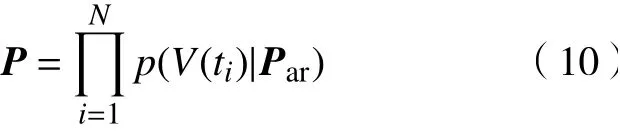
Fisher 信息矩阵是有关P 的期望,可由式(11)表示。根据文献[8]可进一步得到式(12)。可见,Fisher 信息矩阵的值 FIM越大,说明P 越大,输出V的概率越大,表明对该参数组的辨识结果越可靠。

文献[8−9]给出了判断可辨识性的RDE 准则(使得参数组出现概率最大化的计算准则)。

式中:Si为相对敏感度; ∥Par∥2为欧式2 范数,用于将参数向量 X归一化,消除不同参数的不同数量级对RDE 的影响;分子为FIM 矩阵的行列式值D 和 ∥Par∥2的 乘 积;分 母 为FIM 矩 阵 的 条 件 数mod E,由矩阵的最大特征值与最小特征值的比值得出,用于判断参数之间的相关性。
当D 越大,mod E越小,即RDE 越大时,获得的辨识参数组越优。
参数敏感性分析步骤如图2 所示,首先排除表1 中的电池尺寸参数 L , A,以及其他容易获得的 参 数 θ0,θ100,σ,k 和 α。将SP2D 模 型 中 剩 余的17 个参数(对应A-A 中的参数)随机组合进行计算。K 为卡尔曼增益系数,S 为电池电量。图3 是以不同参数为基参数的参数组的RDE。可见,不论以哪个参数为基参数,随着参数数量的增加,RDE 均呈先增大再减小,且在10 个参数数量时达到最大。以RDE 最大的参数组为最优参数组,即表3 中的参数组B-B。在表3 中,参数组C-C 为辨识性差的参数组。
2.2 参数辨识
根据参数可辨识性分析结果,对最优辨识参数组B-B 采用非线性最小二乘法进行辨识,式(14)为目标函数。其中, Vm为电池模型输出的电压,Vref为参考电压, J为雅可比矩阵。利用预测电压和参考电压的误差修正参数,式(15)为误差修正的迭代公式。

图2 基于SP2D 模型的SOC 估计策略Fig.2 SOC estimation strategy based on the SP2D model
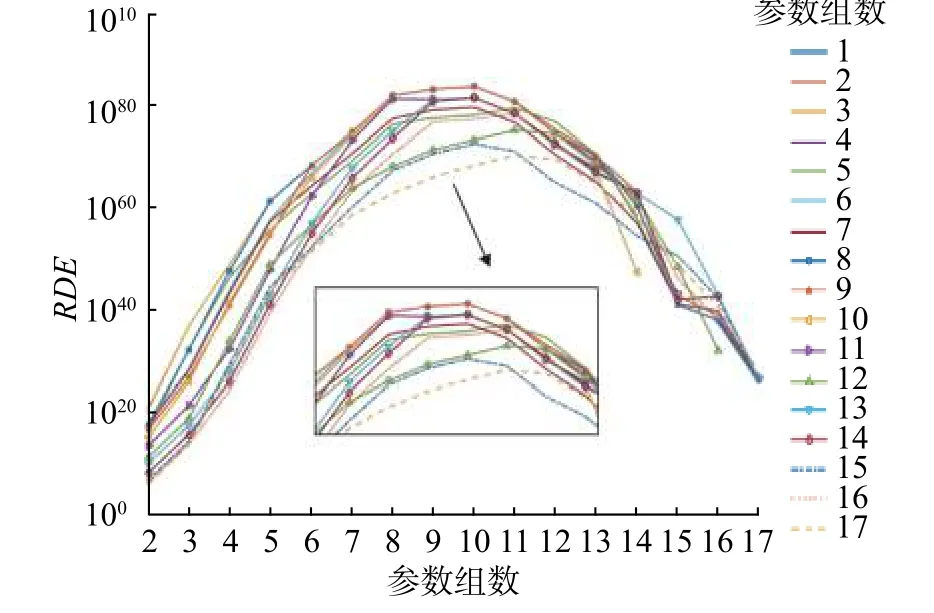
图3 参数组敏感度分析Fig.3 Parameters sensitivity analysis

式中: ∆θ为 误差修正量; λ为时间步长。
假定表1 中的参数值为真值,可将SP2D 模型在真值参数下的输出电压作为参考电压。这里为了单纯验证本文的参数辨识方法,人为使参数组B-B 中待辨识参数存在明显误差,将其初值设为真值的5 倍(记为 Pare)。选择FUDS 工况下,对2 个相同的SP2D 模型进行比较。考虑到本文中的电池为锂离子电池,在放电中期存在电压平台,可辨识性较差,因此,宜选取放电初期或充电初期(本文选择测试工况的前1 200 s,初始S=1)进行参数辨识。
为了阐述方便,将最优参数组B-B 表示为向量 Par10=[ εe,p, εe,s, kp, Ds,n, kn, ce,0, cs,max,n, Ds,p, Rint,De]。辨识策略,如图2 所示,辨识结果如图4 所示。图4(a),4(b),4(c),4(d)分别对应向量Par10 ,Par9(去 掉 Par10中 的 ce,0),Par8( 去 掉 Par10中的 Ds,p)和 Par7( 去掉 Par10中 的 cs,max,n)的辨识结果,横坐标为参数组数(按照向量中参数的顺序),纵坐标为参数误差,用差值的绝对值与真值的比值来表示。随着参数减少,辨识误差减小。当参数组减为 Par7时,平均误差和最大误差分别小于3%和15%(图4(d)),说明这组参数组通过辨识,可以获得和真值很接近的辨识结果。
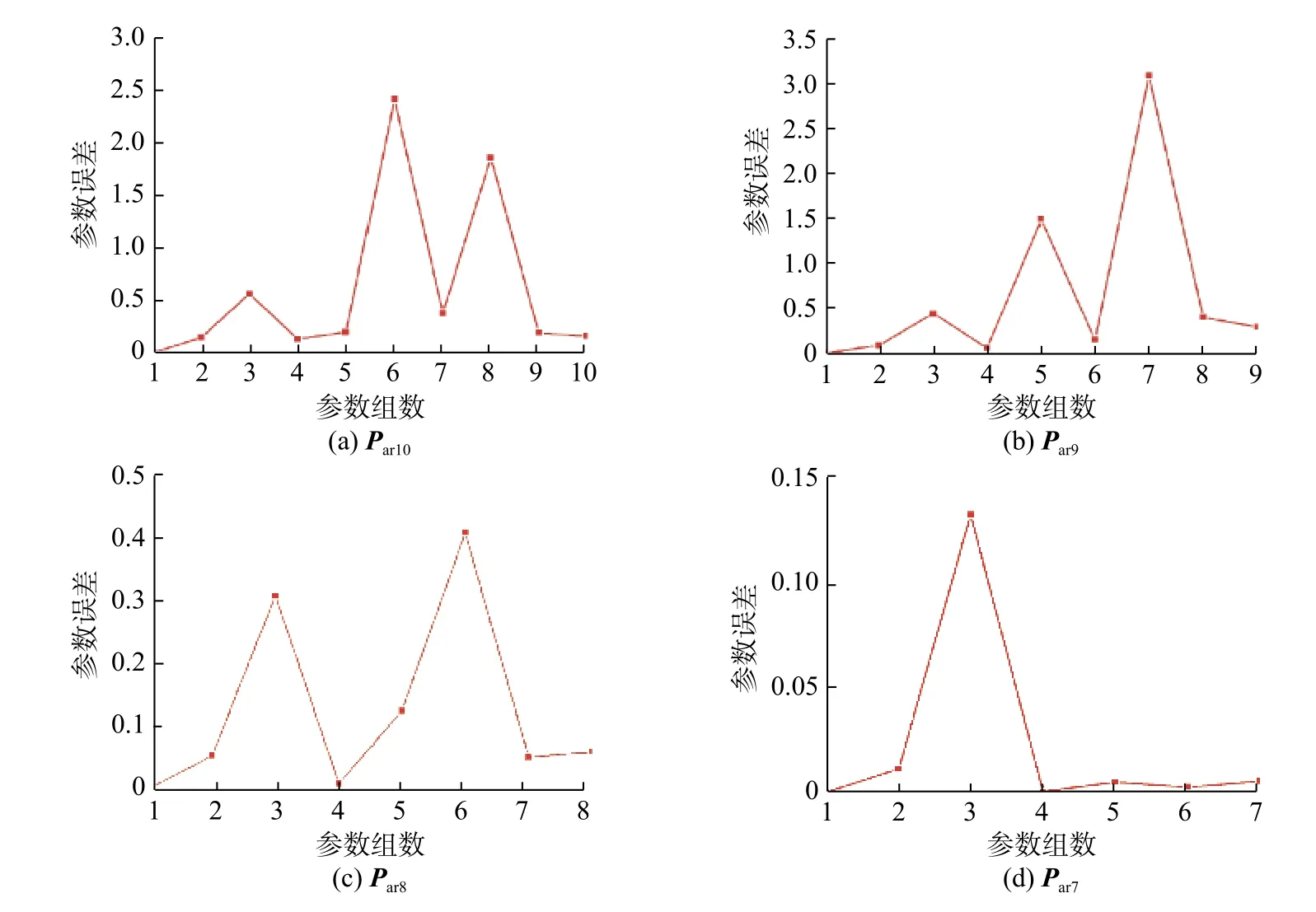
图4 辨识结果误差分析Fig.4 Error analysis of the identification results

图5 SP2D 模型在辨识参数与真值参数下的输出电压对比Fig.5 Comparison between the output voltages of the SP2D model with identified parameters and original parameters
图5 为不同辨识参数组下SP2D 模型的输出电压和参考电压的对比分析。图5(b)是图5(a)的局部放大。其中,V-Correct 为参考电压Vref,V-17,V-10,V-8,V-7 和V-0 分别是辨识参数组 Par17,Par10,Par8,Par7,Pare后 的电压 Vm曲线,Verr 为电压误差。可见,在17 个参数同时辨识下(图5(d)),模型输出电压与参考电压的误差虽比使用错误参数Pare时达到300 mV 的误差有所改善,但仍达100 mV,这是由于有些参数可辨识性差,难以准确辨识,同时也会影响其他可辨识性好的参数的辨识,使得模型估计不准。而采用可辨识性分析后的参数组 Par10和 Par8进行辨识时,误差明显减少(图5(b)和5(c)),最大误差只有0.3 mV。当只辨识 Par7时,模型输出电压与真值参数下的模型输出电压基本一致,可将误差进一步显著减小至0.05 mV 以内。
3 基于SP2D 模型的电池SOC 估计及实验验证
3.1 SOC 在线估计
基于SP2D 模型与参数辨识,采用自适应卡尔曼滤波进行SOC 估计。

式中: θave为粒子平均浓度与最大浓度的比值;qn, qp为负极和正极的固相体积平均浓度流。
取 状态 参 数 x=[S,qn,qp]。一般 情况 下,卡 尔曼滤波可表达为[8]

式中:A 为状态转移矩阵;B 为输入矩阵;C,D 为 预 测 矩 阵; wk−1为 过 程 噪 声; vk−1为 观 测 噪声; N(0,Q)表 示正态分布; Kk为卡尔曼滤波系数; Pˆk为 协方差;u 为输入(取电流值); V为输出值;k 为迭代次数; ∧符号表示预测值。
由 于 在 实 际 应 用 中,wk−1,vk−1不 能 准 确 知道,其偏差随着数据量的增加会累积,影响估计精度。因此,本文采用自适应卡尔曼滤波的方法[10],根据预测与实测数据的误差 ε修 正 wk−1,vk−1的值,来降低噪声对预测的影响,递推公式为


式中: ε为误差向量; Q,R为噪声的方差。
3.2 实验验证
采用Digatron Firing Circuit(德国)公司生产的Digatron 多功能电池测试仪UBT300-060,将电池放置在25 ℃恒温箱内,选择FUDS 循环工况,先将电池充满(S=1)后测试直到截至电压(S=0),将采集得到的电压及电流作为模型参考电压及输入电流。
图6 为模型输出与实验值的对比。其中,Real-U 和SOCr 分别表示为电池输出电压和SOC实测的实验值;U 和SOC 分别表示为基于表1 中参数的SP2D 模型的输出电压和SOC 估计值;UIden 和SOC-Iden 分别表示采用本文参数辨识策略,以Real-U 为参考电压,对参数向量 Par7进行辨识后的模型(SP2D-Iden)输出电压和SOC 估计值。Ue为电压误差,Ue-Iden 为参数辨识后的电压误差。由图6 可见,辨识参数后,SP2D 模型提高了精度,电压曲线更加接近实际曲线,平均误差由50 mV 降到了18 mV,而SOC 也与实际值基本一致,平均误差小于0.1%。上述结果验证了本文提出的参数辨识策略应用在实际电池上的有效性。
为了考察对初始SOC 误差的校正能力,设定初始误差为0.2,再基于SP2D-Iden 模型进行SOC在线估计,并对比基于等效电路模型(一阶ECM)下的SOC 估计方法,如图7 所示。SP2D-Iden比ECM 的电压预测精度更高,2 个模型的电压平均误差分别为19 mV 和37 mV。且基于SP2DIden 的SOC 平 均 误 差 为1.2%, 基 于ECM 的SOC 平均误差为1.7%。即基于SP2D-Iden 可将电压平均误差减小48.6%,SOC 平均误差减小29.4%。这里等效电路模型采用的是常用的一阶RC 模型(电阻电容回路模型),其电压预测的误差较大。使用二阶或者更复杂的等效电路模型,电压精度可以接近SP2D 模型的精度。
进一步分析可知,2 种方法下SOC 都能快速修正到正确值附近,但对影响电池容量利用率的关键阶段——电池放电的中后期(S<0.4):基于ECM的SOC 估计误差较大,SOC 平均误差为2%,最大误差达4.4%;而SP2D-Iden 模型在此较低的SOC 区间也能够保持很好的估计精度,SOC 平均误差仅0.7%,最大误差1.8%。即在电池放电的中后期,基于SP2D-Iden 模型可将电池SOC 估计的平均误差、最大误差分别减小65%和59.1%。这说明本文方法可明显减小电池在整个工作范围内的SOC 估计误差。

图6 SP2D-iden 模型与电池实验对比Fig.6 Comparative analysis between the results of the SP2D-Iden model and battery experiments
图7 SP2D-iden 模型与等效电路模型对比Fig.7 Comparative analysis between the results of the SP2D-Iden model and equivalent circuit model
4 结 论
在电池SP2D 模型的基础上,对模型参数进行可辨识性分析,提出了利用非线性最小二乘法结合Fisher 信息矩阵的参数辨识方法。仿真结果表明,该辨识方法可以减小参数辨识的误差,使平均误差减小至3%以内,进而提出了基于电化学SP2D-Iden 模型的SOC 在线估计方法。实验表明,相比目前常用的基于ECM(一阶RC)的SOC估计方法,本文SP2D-Iden 模型可将电池电压平均误差减小近50%,同时提高SOC 估计精度近30%。而在电池放电中后期(S<0.4)SP2D-Iden 模型仍能保持较高精度,相比ECM 模型,SOC 估计精度提高了60%以上,这证明了本文SOC 估计方法对整个SOC 范围内的高精度估计特点。
